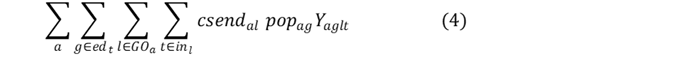1. INTRODUCCIÓN
En Paraguay, hasta el año 2016, se asignaba el 3,44% del PIB al gasto público en educación, del cual, el 92% se empleó para el pago de salarios. Aunque las inversiones en infraestructura escolar se han incrementado en los últimos años1, existen dificultades relativas a los límites presupuestarios, la planificación estratégica del dimensionamiento de la infraestructura escolar, y la orientación de las inversiones.
El Ministerio de Educación y Ciencia (MEC) del Paraguay ha elaborado la metodología de Micro planificación de la Oferta Educativa a fin de planificar de forma efectiva y eficiente las políticas educativas, apuntando, por ejemplo, a mejorar las condiciones de enseñanza-aprendizaje de las instituciones. Lo anterior se lograría a través de la mejora de la infraestructura edilicia y la dotación de medios educativos para los estudiantes y los docentes2.
La toma de decisiones para la localización de establecimientos escolares puede realizarse con criterios cuantitativos, tomando en cuenta las restricciones logísticas y presupuestarias del sistema educativo. De esta manera, se puede obtener soluciones eficientes para distintos escenarios de transformación de la infraestructura.
En este contexto, las buenas soluciones ayudan a minimizar los costos de mantenimiento de infraestructura y direccionar las inversiones en obras que beneficien a un mayor número de estudiantes. Por lo tanto, es pertinente investigar estrategias para la reorganización, ampliación y cierre de establecimientos escolares, asignando los recursos disponibles de la mejor manera posible.
Con una mirada a corto plazo en la calidad de la educación, una buena infraestructura escolar puede generar situaciones favorables para un aumento del rendimiento escolar satisfaciendo el derecho de los estudiantes a acceder a espacios físicos convenientes para su aprendizaje3. Luego, en un horizonte más a largo plazo y más allá del incremento de ingresos monetarios que puede aportar una buena educación de las personas, subyacen otros beneficios importantes como la reducción de la pobreza y la desigualdad4.
En particular, analizando el caso de estudio de los distritos del Departamento de Caazapá que cuenta con 469 establecimientos escolares, se identificó que un 57% solicitó reparaciones edilicias y el 40% solicitó la construcción de nueva infraestructura para el año lectivo 20195. Además, en un 66% de establecimientos hay subutilización de la capacidad, con menos de 25 alumnos por aula, y en un 1% sobreutilización, con más de 49 alumnos por aula6,7,8.
Con este trabajo se generó un conjunto de establecimientos escolares, reorganizados, que minimiza los costos operativos, de mantenimiento, de transporte y de inversión para satisfacer la demanda educativa en los distritos del departamento de Caazapá, mediante la identificación, adaptación y aplicación de un modelo de programación matemática. Para resolver este problema se determinó las necesidades de infraestructura, y se estimaron la demanda y los costos para cada establecimiento escolar.
Los resultados obtenidos pueden utilizarse como un punto de referencia para visualizar oportunidades de mejora en la red educativa, a fin de ejecutar adecuadamente las inversiones y reducir el costo de operación del sistema.
2. METODOLOGÍA
Esta investigación es de naturaleza descriptiva con un enfoque cuantitativo. Para la obtención de datos, en una primera instancia, se entrevistó a los agentes involucrados en la planificación de la oferta educativa del Ministerio de Educación y Ciencias (MEC).
Luego, se relevaron datos mediante una encuesta aplicada a 339 establecimientos escolares en el departamento de Caazapá, con el objetivo de determinar sus condiciones de infraestructura. Se recopiló datos de matrículas del Registro Único del Estudiante (RUE) del Departamento de Estadística Aplicada6,7,8 y se estimaron los costos de infraestructura a partir de presupuestos elaborados por la Dirección de Infraestructura del MEC9.
Buscando identificar un modelo matemático acorde a las características del sistema educativo paraguayo, se revisó la literatura existente sobre problemas similares y abordados con diferentes técnicas de Investigación de Operaciones10-14. Además, se establecieron las etapas de un estudio de Investigación de Operaciones, conceptos, clasificaciones y técnicas de resolución de modelos matemáticos, y metodologías utilizadas para la ubicación/localización de establecimientos escolares15-17.
Araya18 realizó una investigación para resolver el problema de la distribución poco eficiente de escuelas en zonas rurales de Chile. Se realizaron modificaciones a este modelo matemático, adaptándolo a las particularidades del sistema educativo de Paraguay y a las características de la situación de la comunidad del caso de estudio.
Se ejecutaron cuatro fases para el proceso de adaptación del modelo, según algunos de los lineamientos de Taha19:
Definición del problema.
Identificación del modelo.
Solución del modelo.
Validación del modelo original con datos del caso de estudio.
Se programó y resolvió el modelo con el lenguaje de programación matemática algebraica ILOG® IBM CPLEX 12.6. Se empleó Microsoft Excel® 2019 para procesar, resumir y analizar los datos, y la herramienta de gestión de información geográfica QGIS 3.14.10 para graficar los resultados.
Por último, se analizaron los resultados y se elaboró una propuesta de establecimientos escolares que deben seleccionarse, junto con un resumen de los costos del sistema.
2.1. Sobre el modelo matemático identificado
Los problemas identificados por Araya18 incluyen el exceso de distancias recorridas por los estudiantes hasta el local escolar, el empleo desigual de infraestructura, la subutilización y sobreutilización de capacidad en términos de números de alumnos. Como solución se desarrolló un modelo de programación matemática, lineal entera mixta, a fin de optimizar la distribución de escuelas rurales en Chile, de tal manera a asignar eficientemente los recursos y mejorar el sistema educativo en su conjunto.
2.2. Sobre el modelo matemático adaptado
Se adaptó el modelo de Araya18 a las características propias del sistema educativo paraguayo, con las siguientes modificaciones sustanciales:
El problema se reduce a seleccionar/localizar establecimientos existentes para modificar su infraestructura, sin la posibilidad de abrir nuevas escuelas.
Se adaptaron, incluyeron, eliminaron variables y parámetros para representar el funcionamiento de escuelas en dos turnos.
El costo de transporte incluye componentes fijas de inversiones y costos operativos de los medios de transporte necesarios, y una componente variable dependiente de la distancia recorrida y la cantidad de estudiantes que deben viajar.
No se considera necesario segregar a los estudiantes por sus características socioeconómicas para asignarlos a escuelas.
Se considera que los funcionarios podrían ser reasignados a otras instituciones o cargos (tutores pedagógicos, encargados de biblioteca, cargos directivos), por lo que se excluye los costos de liquidación de personal de las escuelas no seleccionadas.
En lo que respecta al cálculo de los costos operativos de las escuelas y costos anuales de inversión, se empleó la misma metodología utilizada por Araya18.
2.3. Especificación detallada del modelo matemático adaptado
a) Subíndices del modelo
b) Conjunto de índices del modelo de localización
t ∈ in 1: Modalidades de escuelas que son opciones en los establecimientos «l»
g’ ∈ grade gt : Grados que pueden estar junto con grado «g» para institución de modalidad «t» (en caso de haber plurigrado)
a ∈ SA c : Conjunto de paradas “a” que son parte del distrito «c»
l ∈ SL c : Conjunto de establecimientos “l” que pueden ser elegidos en el distrito «c»
l ∈ GO a : Conjunto de establecimientos «l» que son opciones para estudiantes del origen «a»
a ∈ GO l : Conjunto de establecimientos escolares «a» que puede enviar estudiantes al establecimiento «l»
a ∈ ed t Conjunto de grados escolares “g” que pueden enseñarse en una escuela de modalidad «t»
c) Variables de decisión
X lt : Variable binaria que asume el valor 1 si una institución de modalidad «t» funciona en el establecimiento «l» y 0 en caso contrario (X lt ∈{0,1}).
Y aglt : Fracción de estudiantes del establecimiento «a», grado «g» asistiendo a el establecimiento «l» funcionando en modalidad «t»,(0 ≤ Y aglt ≤1).
Z al : Variable binaria que asume 1 si existe asignación de estudiantes del establecimiento «a» al destino «l» y 0 en caso contrario (Z al ∈ {0,1}).
ADD lgt : Cantidad de secciones de grado «g» a abrir en la institución de modalidad «t» en el establecimiento «l» (Secciones).
SUP lgt Cantidad de secciones de grado «g» a eliminar en la institución de modalidad «t» en el establecimiento «l». (Secciones).
CONSl: Número de aulas a construir en el establecimiento «l» (Aulas).
S lgt : Porcentaje extra para agregar a cursos existentes de grado «g» en la institución de modalidad «t» en el destino «l». (%).
d) Función Objetivo
La función objetivo es una función de costos del sistema educativo que contiene las siguientes componentes:
El primer término (1) corresponde a los costos operativos y de inversión en infraestructura en que se incurren al seleccionar los establecimientos.
Luego, la expresión (2) incluye los costos de inversión “𝑐𝑜𝑠𝑡𝑏𝑢𝑠” en caso de que se asignen estudiantes desde la parada 𝑎 al establecimiento 𝑙. Esto es necesario porque se trabaja con el supuesto de que los estudiantes serán transportados en un bus que será adquirido con presupuesto del sistema educativo.
El término (3) se utiliza para imputar el costo de operativo del bus en la ruta que hace desde la parada 𝑎 al establecimiento 𝑙.
La expresión matemática (4) mantiene la nomenclatura utilizada por Araya 18 para los costos de transporte, pero adquiere una interpretación distinta, en este caso representa el costo operativo adicional del bus en que se incurrirá por cada estudiante a transportar desde la parada 𝑎 hasta el establecimiento 𝑙. Este costo es proporcional a la cantidad de alumnos que deben viajar.
La expresión (5) se utiliza solo para incluir los costos operativos en que se incurren al añadir una nueva sección. Los costos de construcción de las aulas se incluyen por separado.
Luego, el término (6) representa la suma de los costos incurridos en la construcción de aulas en los establecimientos. Se incluye esto, para separar el costo de construcción de un aula del costo de añadir una sección, porque en el modelo adaptado la cantidad de aulas a construir es independiente al número de secciones a añadir, por la particularidad de los turnos.
El termino (7) se utiliza para incluir el costo negativo que se genera al eliminar una sección.
Por último, se incluye el término (8) para penalizar las asignaciones en secciones donde se exceden la capacidad de las aulas dentro de un límite establecido.
e) Restricciones
Las restricciones del modelo totalizan 19 conjuntos que incluyen restricciones respecto a la demanda, la modalidad de las escuelas, la capacidad de las aulas, el presupuesto disponible por distrito, asignaciones incompatibles y la naturaleza de las variables.
A continuación, se enuncian dichas restricciones:
Todos los estudiantes deben ser asignados a una escuela.
Las escuelas solo pueden funcionar en una de las modalidades que son opciones para ese establecimiento.
No se puede exceder la capacidad de las aulas para las escuelas plurigrados.
No se puede exceder la capacidad de las aulas para las escuelas monogrado.
No se puede exceder el número de aulas disponibles.
Solo se puede eliminar cursos en modalidades de establecimientos seleccionados.
Solo se puede construir un número máximo de aulas.
No se puede exceder el presupuesto total. Los costos de operaciones, implementación, transporte, agregar y quitar cursos, deben estar dentro del presupuesto de cada distrito.
No se puede exceder el presupuesto de implementación.
No se puede exceder el presupuesto de operaciones.
No se puede exceder el presupuesto de transporte.
Una escuela nueva no puede ser plurigrado si sobrepasa un cierto número de alumnos asistiendo.
No se puede cerrar más de un determinado número de instituciones establecido por el ministerio.
La variable de holgura para un grado en una escuela determinada sólo puede existir si la misma está abierta y si tiene cursos de este grado en particular. Esta holgura debe ser menor a un límite establecido.
No se puede asignar estudiantes a escuelas que funcionan en modalidades no compatibles con el establecimiento.
No se puede asignar estudiantes a grados de escuelas que son incompatible con la modalidad que es seleccionada para el establecimiento.
Los estudiantes no pueden viajar una distancia superior a la máxima permitida.
Restricción auxiliar para introducir los costos de transporte.
Naturaleza de las variables.
3. RESULTADOS
3.1. Indicadores demográficos
Según datos de la Dirección General de Estadística, Encuestas y Censos20, la población con edad menor a 15 años se caracteriza por una tendencia a disminuir, ya desde la década de los 80. Esta información es relevante, pues consiste en una población en etapa escolar, y en términos de planificación debe considerarse la capacidad de infraestructura en el mediano y largo plazo.
3.2. Situación de la infraestructura
En el departamento de Caazapá, se observa un exceso en la oferta de escuelas con pocas aulas en zonas rurales, además de un considerable déficit en términos de infraestructura de establecimientos educativos y del presupuesto para mantención de estos.
Se visualiza que el 31% de las escuelas rurales tiene menos de 4 aulas, siendo 5 el número de aulas por establecimiento, en promedio. El bajo número de aulas por escuela incrementa la demanda de establecimientos escolares necesarios para satisfacer los requerimientos de alumnos, generando inconvenientes en la gestión de recursos y excesos de costos en el sistema global.
Además, se tiene evidencia de cierta deficiencia sostenida en la cobertura de servicios básicos. En este sentido, el 3% de las escuelas del departamento de Caazapá no cuenta con energía eléctrica, el 27% no cuenta con servicio de agua potable y el 26% no posee baño moderno.
3.3. Resultados para el Departamento de Caazapá
En la Tabla 1, se resumen los resultados del modelo matemático para el Departamento de Caazapá.
Al reorganizarse los establecimientos escolares estos disminuyen en menos del 50% de los que se encuentran en funcionamiento actualmente, por tanto, fueron seleccionados 228 locales de 455 disponibles. Al mismo tiempo, se reduce el número de escuelas plurigrado de 182 a 59.
Tabla 1 Resumen de resultados del modelo en el departamento de Caazapá
| Escenario Actual | Escenario optimizado | ||
|---|---|---|---|
| Establecimientos Escolares | Existentes | 454 | 454 |
| Seleccionados | - | 228 | |
| Plurigrados | 182 | 59 | |
| Secciones | Agregados | - | 74 |
| Eliminados | - | 2 | |
| Nro. de alumnos por establecimiento | 89 | 177 | |
| Capacidad ociosa existente | 74% | 40% | |
| Nro. de alumnos por profesor | 9 | 14 |
Fuente: Elaboración propia.
Los principales beneficios serían la reducción de la capacidad ociosa en un 34%, el incremento del promedio de estudiantes por escuela de 89 a 177 y el aumento de alumnos por sección de 9 a 14.
Como consecuencia de estas modificaciones se reducirían en un 55% los costos de adecuación y reparación de aulas y sanitarios, y en un 38% los costos de inversión en mejoras. También se dispondría del 28% de los salarios que podrían reasignarse a nuevas funciones.
Sin embargo, se debería incurrir en costos de transporte, los que representan el 20% del ahorro total que se tendría en las inversiones de reparación y construcción de nueva infraestructura.
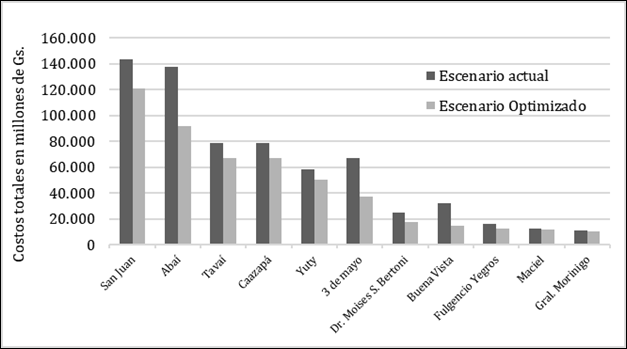
En la Figura 1, se observan los costos totales por distrito de la operación del sistema educativo para los escenarios actual y optimizado.
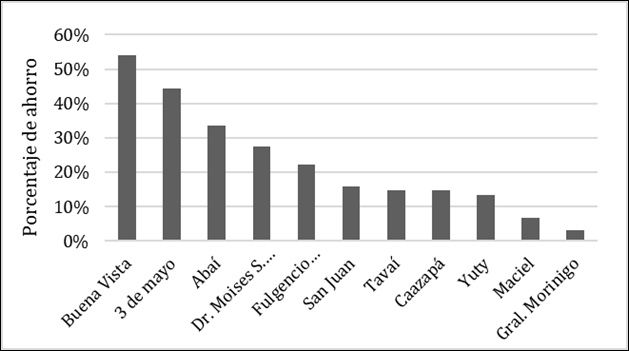
En la Figura 2 se observa para cada distrito el ahorro que se obtendría en el escenario optimizado respecto al escenario actual, siendo el promedio de 23% de ahorro.
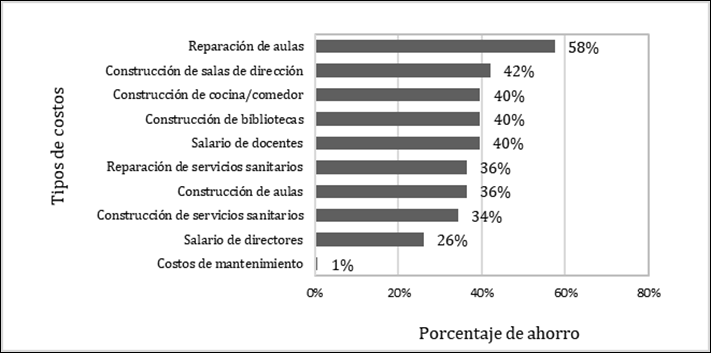
En la Figura 3 se observa para el escenario optimizado el ahorro por tipo de costo. El ahorro promedio es de 47% en costos de reparación y 38% en costos de construcción.
3.4. Resultado para un distrito del departamento de Caazapá
A continuación, sigue una muestra del resumen de resultados para uno de los distritos del departamento de Caazapá.
En el distrito de Caazapá fueron seleccionados 21 de los 70 establecimientos escolares candidatos, de los cuales 3 funcionarían en la modalidad de enseñanza plurigrado. Además, se añaden 6 secciones nuevas sin eliminar ninguna de las existentes.
La Tabla 2. Resumen de resultados para el distrito de Caazapá detalla los resultados más relevantes para este distrito.
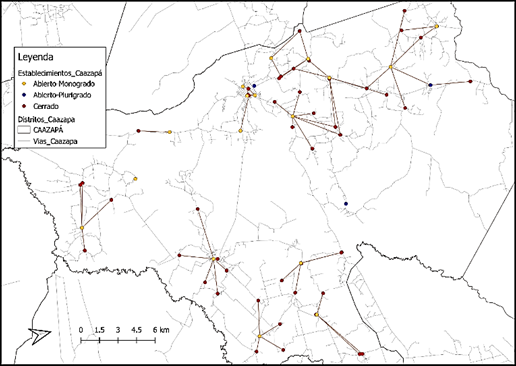
En la Figura 4 Establecimientos escolares seleccionados en el distrito de Caazapá se muestra los establecimientos seleccionados en este distrito (nodos de color amarillo y azul), también se observa los establecimientos que no son elegidos (nodos en color rojo), y la asociación de escuelas (representadas mediante una línea recta) para atender a la demanda de estudiantes de acuerdo con la capacidad de cada establecimiento. Distribuciones similares fueron obtenidas para cada uno de los distritos del Departamento.
Tabla 2 Resumen de resultados para el distrito de Caazapá.
| Escenario Actual | Escenario optimizado | ||
| Establecimientos Escolares | Existentes | 70 | 70 |
| Seleccionados | - | 21 | |
| Modalidad | Monogrado | 29 | 18 |
| Plurigrado | - | 3 | |
| Secciones | Agregadas | - | 0 |
| Eliminadas | 0 | 0 | |
| Nro. de alumnos por establecimiento | 108 | 247 | |
| Capacidad ociosa existente | 73% | 28% | |
| Nro. de alumnos por profesor | 13 | 20 |
Fuente: Elaboración propia.
4. CONCLUSIÓN
El presupuesto estimado para la adecuación de todas las escuelas supera los recursos con los que se cuenta actualmente. Es posible disminuir estos costos priorizando los establecimientos seleccionados con la propuesta de reorganización que se presenta en este trabajo, redistribuyendo las matrículas de las escuelas e incurriendo en costos de transporte.
Puntualmente, se adaptó el modelo de Araya18 considerando las condiciones particulares del escenario en el que se desarrolló el estudio. El modelo fue resuelto utilizando el programa IBM ILOG Cplex Optimizer V 12.6, fijando el objetivo de minimizar los costos estimados para cada distrito del Departamento de Caazapá.
La propuesta de este trabajo selecciona aproximadamente la mitad de las escuelas existentes, es decir, un total de 228 establecimientos escolares, de los cuales 59 de ellos son escogidos para funcionar en la modalidad plurigrado, una cantidad 30% menor al número de escuelas plurigrados que existen actualmente.
La capacidad ociosa con la nueva distribución de establecimientos se reducirá de 74% a 40%. Esto se consigue aumentando el número promedio de alumnos por sección de 9 a 14 e incrementado el número promedio de alumnos por establecimiento a un 98%.
Con la reorganización de establecimientos será posible disminuir los presupuestos estimados para la mejora y adecuación de establecimientos escolares en un 55%. También quedará disponible para reasignar un 28% de salarios en otras funciones, evitando despidos. El costo de transporte incurrido en la redistribución de los estudiantes representa el 7% del presupuesto total estimado para el departamento y es equivalente al 20% del ahorro que se puede conseguir en costos de inversión en infraestructura. Finalmente, el costo total estimado para el sistema educativo se reduciría en 24% con relación al costo actual.
Las soluciones presentadas son representativas para el problema real, pues para la estimación de los presupuestos y para el cálculo de los costos fueron considerados costos de referencia y promedios, en base a datos oficiales que fueron procesados. Por lo tanto, estas estimaciones y cálculos pueden ser utilizados como guía para el diseño de redes más eficientes.











 uBio
uBio