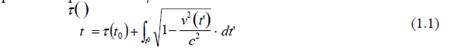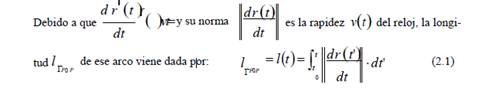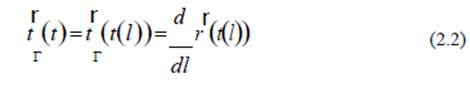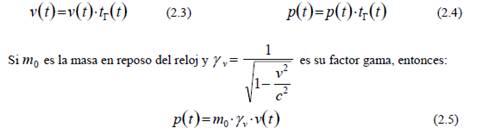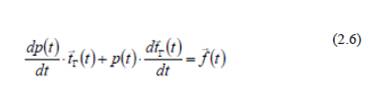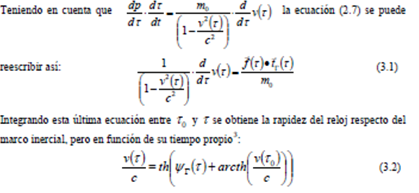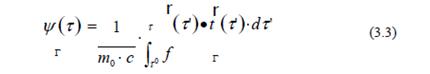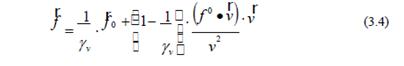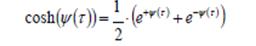1.-INTRODUCCIÓN
Unus mundus, que en latín significa "un mundo", es el concepto de una realidad subyacente unificada de la que todo emerge y a la que todo regresa. Restringido al dominio de la Física, alude al postulado según el cual todos los observadores en el universo, con in- dependencia de su estado de movimiento, deben estar de acuerdo sobre la ocurrencia de ciertos sucesos, tales como explosiones e implosiones, nacimientos y muertes.
Este postulado se encuentra en la base de la formulación original de la teoría restringida de la relatividad que, entre otras cosas, es una teoría de invariantes en el tiempo-espacio plano1.
En la teoría restringida de la relatividad, a diferencia de lo que acontece en la teoría generalizada, se hace una distinción entre marcos de referencia inerciales y marcos de referencia no inerciales. La descripción del movimiento de un reloj realizada por un observador inercial (es decir, un observador fijo a un sistema inercial) es generalmente mucho más simple que la descripción realizada por un observador fijo a un sistema de referencia no inercial. En la teoría restringida es posible escribir las ecuaciones de las leyes físicas res- pecto de sistemas de referencia no inerciales, hacienda una descripción en el espacio- tiempo plano de Minkowski. Se debe introducir un tensor métrico en este espacio plano, empleando herramientas matemáticas que tienen un cierto parecido con las que se emplean en la teoría generalizada de la relatividad2,4.
Ahora bien, cuando se considera el transcurso del tiempo propio para los relojes que se encuentran acelerados respecto de un observador inercial, se encuentra un problema interesante, que parece contradecir el postulado de unidad del tiempo-espacio.
Comencemos considerando un observador inercial que registra el movimiento de un reloj acelerado.
Convengamos que un reloj es cualquier dispositivo físico que se puede considerar como una partícula, que sigue una línea de universo temporaloide y que genera una secuencia de eventos llamados tics. Un reloj ideal es un reloj tal que el tiempo propio transcurrido entre dos tics (no necesariamente consecutivos) es proporcional al número de tics entre el primer tic y el último tic considerado, con el mismo factor de proporcionalidad en cada punto de la línea de universo del reloj.
Esta definición presupone definir el tiempo propio transcurrido entre dos eventos, a lo largo de una trayectoria temporaloide en el espacio-tiempo de Minkowski, como la longi tud del segmento de la línea de universo entre estos dos eventos determinada a partir del tensor métrico en ese espacio-tiempo4.
Entonces, un reloj ideal es un reloj que mide el tiempo propio. Si se describe, respecto a un sistema inercial, una línea de universo formada por eventos en el espacio-tiempo de Minkowski, se puede calcular el tiempo propio a lo largo de esta línea de universo mediante una fórmula que relacione el tiempo propio con el tiempo inercial.
De acuerdo con la hipótesis del reloj, si un reloj ideal se mueve de manera no uniforme a través de un marco inercial, la aceleración como tal no tiene efecto en la cadencia del reloj: su ritmo en un instante respecto de un sistema inercial depende solo de su velocidad en ese mismo instante respecto de ese sistema inercial.
Se supone que el ritmo del reloj acelerado es idéntico al ritmo de un reloj fijo al marco inercial que en el instante considerado se encuentra en co-movimiento con el reloj acele rado.5,7.
Entonces, en el marco de la teoría restringida de la relatividad y aceptando la hipótesis del reloj, el tiempo propio para todos los observadores acelerados viene dado como función del tiempo inercial por la Fórmula1:
En (1) la velocidad de la luz en el vacío viene representada por c, mientras que t0 es el
valor inicial del tiempo inercial t y v(t) es la historia de rapidez del reloj acelerado, respecto del sistema inercial de referencia. La rapidez se define como v = ॥v r ॥ , donde ॥v r ॥ es la norma del vector velocidad v .
Si la masa propia del reloj es diferente de cero, su historia de velocidad debe verificar la desigualdad estricta v(t)< c, para cada instante de tiempo inercial.
En 1984 José Ferrari concibió una posibilidad interesante: que la función v(t ) se aproxime a su cota superior c tan rápido como para que
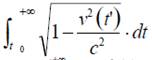 resulte convergente. Si así fuera, definamos:
resulte convergente. Si así fuera, definamos:
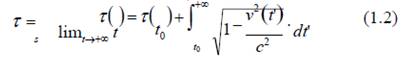
Entonces resultaría imposible asignar un instante de tiempo inercial t
tiempo propio t ˃. t s
Una condición necesaria para que un observador fijo al sistema de referencia inercial y un observador que se mueve con el reloj acelerado se puedan poner de acuerdo acerca de la ocurrencia de ciertos eventos, tales como explosiones e implosiones, nacimientos y muertes, es que exista una correspondencia uno a uno entre cada instante de tiempo t y cada instante de tiempo.
De (1) se desprende que
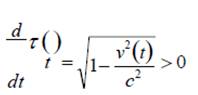 de modo que la correspondencia entre los instantes de tiempo inercial y los correspondientes instantes de tiempo propio para el reloj acelerado es uno a uno. Hasta este punto, todo bien.
de modo que la correspondencia entre los instantes de tiempo inercial y los correspondientes instantes de tiempo propio para el reloj acelerado es uno a uno. Hasta este punto, todo bien.
Pero admitamos, como se hace en casi todas las ramas de la Física, con excepción de la Cosmología y tal vez, la Astrofísica, que el tiempo no está acotado. Entonces, si la integral del tiempo propio
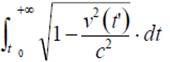 resulta ser convergente y si, además, suponemos que el tiempo propio no está acotado, parte de la experiencia del observador acelera- do junto con el reloj debe ocurrir fuera del universo del observador fijo al sistema inercial. Los nacimientos y las muertes, las explosiones y las implosiones que pudieran ser parte de la experiencia del observador fijo al reloj acelerado para instantes de tiempo propio posteriores a s no podrían ser parte de la experiencia del observador inercial.
resulta ser convergente y si, además, suponemos que el tiempo propio no está acotado, parte de la experiencia del observador acelera- do junto con el reloj debe ocurrir fuera del universo del observador fijo al sistema inercial. Los nacimientos y las muertes, las explosiones y las implosiones que pudieran ser parte de la experiencia del observador fijo al reloj acelerado para instantes de tiempo propio posteriores a s no podrían ser parte de la experiencia del observador inercial.
Así pues, parece que tenemos un problema, muy diferente a la paradoja de los gemelos2.
Este problema motivó una breve discusión en una carta al Nuovo Cimento8.
Con el propósito de aportar una solución preliminar, en la carta mencionada se contemplaron dos puntos de vista alternativos:
La hipótesis del reloj es solo una aproximación, válida si se cumplen ciertas restricciones.
Dicha hipótesis es siempre aplicable, pero en la naturaleza solo podemos encontrar campos de fuerza respecto del observador inercial tales que
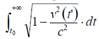 siempre resulte ser divergente.
siempre resulte ser divergente.
Este trabajo persigue los siguientes objetivos:
Profundizar la investigación de la relación, relativa a un observador inercial, entre la 3-fuerza relativista que actúa sobre el reloj ideal acelerado y la integral del tiempo propio como función del tiempo inercial. Esto se hace en la sección 2.
Relacionar la convergencia de la integral del tiempo propio con el comportamiento de la 3-aceleración propia del reloj. Este problema se estudia en la sección 3.
Comparar los resultados obtenidos para la relación entre tiempo propio y tiempo inercial para el movimiento de un observador considerado como una partícula acelerada en un espacio de curvatura nula, con la relación entre el tiempo propio y el tiempo inercial durante la caída de un observador, considerado también como partícula, hacia un agujero negro. Esto se lleva a cabo en la sección 4.
Discutir el significado de los resultados obtenidos en un marco más amplio. Esa discusión y algunas conclusiones se presentan en la sección 5.
El límite entre la relatividad especial y la generalizada generalmente se establece basándose en la curvatura del espacio-tiempo, no en una distinción entre observadores acelera- dos y no acelerados2,4.
Debido a esto, el análisis del movimiento del reloj acelerado se realizará en el marco de la relatividad especial. La aceleración del reloj puede tratarse en un sistema inercial: los marcos de referencia acelerados no son necesarios en este caso, aunque se pueden usar en relatividad especial.
En la caída de un reloj ideal hacia un agujero negro los efectos gravitatorios son funda- mentales. Entonces el espacio no se puede considerar plano y la teoría restringida no resulta aplicable. La caída del reloj hacia un agujero negro se analizará en coordenadas de Schwarzschild, en el marco de la teoría general de la relatividad.
2.-LA HIPÓTESIS DEL RELOJ Y EL COMPORTAMIENTO DE LOS CAMPOS DE FUERZA RESPEC- TO DE UN OBSERVADOR INERCIAL
En el trabajo previo sobre el enlentecimiento de los relojes acelerados estudiamos la con- vergencia de la integral del tiempo propio en función del tiempo inercial suponiendo que los relojes se mueven paralelamente a uno de los ejes de coordenadas del marco de refe- rencia inercial8,9.
En esta sección se generaliza la investigación de la convergencia a movimientos cuales- quiera en tres dimensiones espaciales.
2.1. Fuerza dada como función del tiempo a lo largo de la trayectoria del reloj acelerado
Describimos el movimiento de un reloj acelerado (considerado como partícula con masa en reposo m0 ), respecto de un marco inercial S , mediante su vector de posición r? t , que es suponemos es una función regular del tiempo inercial para t t0 .
La trayectoria seguida por el reloj se representa por Г│, mientras que un arco de trayectoria, comprendido entre un punto inicial P0 de coordenadas (t0 r (t0)) y un punto final P de coordenadas ? t,r? t, ser representa mediante ГP0P
La trayectoria del reloj puede pasar por los mismos puntos del espacio 3D-euclídeo más de una vez, como ocurre, por ejemplo, durante un movimiento circular, de modo que un arco de curva puede ser recorrido más de una vez por un arco de trayectoria.
De (2.1) se desprende que:
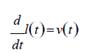 Suponiendo que v(t)˃0 para t ≥ t
0
Suponiendo que v(t)˃0 para t ≥ t
0
la derivada del arco de trayectoria con respecto del tiempo inercial es siempre positiva, de modo que l? t resulta ser una función estrictamente creciente del tiempo inercial. Más aún, supondremos que
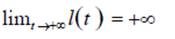
Entonces, la función inversa t t? l existe para todo l 0 y como consecuencia a cada instante de tiempo inercial t t0 le corresponde un valor de longitud de arco de trayectoria l 0 y viceversa.
Introduzcamos ahora el vector unitario tangente en cada punto de la trayectoria:
Entonces la velocidad del reloj v y su cantidad de movimiento p vienen dados por:
De (2.4) se desprende que la versión relativista de la segunda ley de Newton se puede escribir, introduciendo una 3-fuerza relativista f:
En lo que sigue supondremos que la 3-fuerza relativista es una función regular, ya sea del tiempo, ya sea de la posición sobre la trayectoria seguida por el reloj acelerado respecto del marco de referencia inercial S .
Cuando el movimiento provocado por una fuerza dependiente de un potencial se produce en el interior de una región acotada del espacio euclidiano 3-D la integral del tiempo propio diverge siempre y en este caso el problema que motiva este trabajo no se plantea. En todos los casos considerados nada especial, si se exceptúa el orden de infinitud, parece caracterizar el comportamiento de la componente tangencial de la 3-fuerza a lo largo de la trayectoria del reloj acelerado, en relación con la convergencia o divergencia de la inte- gral que da el tiempo propio como función del tiempo inercial. La frontera entre la con- vergencia y la divergencia de esa integral cuando el tiempo inercial tiende a infinito no se encuentra, por ejemplo, entre campos acotados y campos no acotados en el infinito, lo cual sería una diferencia físicamente significativa.
3.- LA HIPÓTESIS DEL RELOJ Y EL COMPORTAMIENTO DE LA ACELERACIÓN PROPIA
Modifiquemos entonces nuestro punto de vista para ver si es posible identificar una diferencia físicamente significativa cuando la 3-fuerza y la 3-aceleración se refieren al propio reloj acelerado.
Como hay una correspondencia regular y uno a uno entre el tiempo inercial t
y el tiempo propio , realicemos un cambio de variable en la ecuación (2.7) considerando que todas las variables dependientes son funciones del tiempo propio del reloj acelerado.
Por definición:
Introduzcamos ahora la familiaS0? t(formada por los marcos de referencia inerciales en co-movimiento con el reloj acelerado. El marco inercial S0? tse mueve, respecto del
marco inercial Sy en el instante t , con la misma velocidad que el reloj, de modo que el reloj se encuentra momentáneamente en reposo respecto de S 0 ? t . Pero como el reloj
está acelerado respecto de S, también lo estará respecto de S 0 ? t . Entonces en un instante
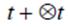 posterior su velocidad respecto de S 0 ? t ya no será nula. Esa aceleración puede medirse mediante un acelerómetro fijo al reloj: es la 3-aceleración propia reloj. (2) (3) (4)
posterior su velocidad respecto de S 0 ? t ya no será nula. Esa aceleración puede medirse mediante un acelerómetro fijo al reloj: es la 3-aceleración propia reloj. (2) (3) (4)
Entre la 3-fuerza relativista f actuante sobre el reloj, vista desde S, y la 3-fuerza relativista f 0 (3-fuerza propia) actuante sobre el reloj, vista desde S0 (t), existe la relación(5):
Como v? tv? t tt(Fórmula(2.3)), formando el producto escalar de ambos miembros de la fórmula (3.4) con el vector unitario tangente a la trayectoria del reloj en el marco S y poniendo el tiempo inercial como función del tiempo propio t t ,se obtiene la notable relación de igualdad entre la componente tangencial de la 3-fuerza relativista y la componente tangencial de la 3-fuerza propia relativista:
De la ecuación que vincula las 3-fuerzas con las 3-aceleraciones obtenemos (5):
De acuerdo con (3.11), tenemos una integral divergente sobre un intervalo de integración finito4, con un integrando positivo que debe presentar una singularidad en T= T s .
El integrando, por la definición usual del coseno hiperbólico como combinación de exponenciales, verifica:
pueda ser convergente, la componente tangencial de la 3-aceleración propia debe presentar una singularidad. Si esa singularidad no existe para un cierto instante T= T s de tiempo propio, ya sea porque
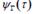 permanece acotada o solamente tiende a infinito cuando
permanece acotada o solamente tiende a infinito cuando
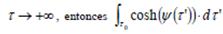 puede tender a infinito solo si tiende a infinito. Pero en este último caso
puede tender a infinito solo si tiende a infinito. Pero en este último caso 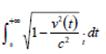 debe ser divergente, y el problema
debe ser divergente, y el problema
En el apéndice C se puede hallar un ejemplo de singularidad en la 3-aceleración propia que conduce a la convergencia de la integral del tiempo propio.
Como consecuencia de lo expuesto en esta sección del artículo, aparece una diferencia
físicamente significativa entre las historias de 3-aceleración propia tangencial
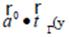 por ende entre las historias de 3-fuerza propia tangencial
por ende entre las historias de 3-fuerza propia tangencial
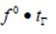 , puesto que
, puesto que
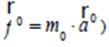 que conduce a un tiempo propio finito para un intervalo de tiempo inercial infinito, y las historias de 3-aceleración propia tangencial (y sus historias de 3-fuerza propia tangencial) que conducen a un tiempo propio infinito para un intervalo de tiempo inercial infinito: una singularidad en la 3-aceleración propia en el primer caso y su ausencia en el segundo caso.
que conduce a un tiempo propio finito para un intervalo de tiempo inercial infinito, y las historias de 3-aceleración propia tangencial (y sus historias de 3-fuerza propia tangencial) que conducen a un tiempo propio infinito para un intervalo de tiempo inercial infinito: una singularidad en la 3-aceleración propia en el primer caso y su ausencia en el segundo caso.
4.-TIEMPO PROPIO Y TIEMPO INERCIAL DURANTE LA CAÍDA DE UNA PARTÍCULA HACIA UN AGUJERO NEGRO
Como se demuestra en el Apéndice D utilizando coordenadas de Schwarzschild, la duración TS del intervalo de tiempo propio que tarda una partícula, que parte del reposo desde una distancia radial r0 respecto del centro de un agujero negro (que no rota), en alcanzar la distancia radial r = rS correspondiente al radio de Schwarzschild del agujero, si se supone que
 es despreciable respecto de la unidad, viene dada por:
es despreciable respecto de la unidad, viene dada por:
Así pues, un cuerpo que se deja caer desde el reposo, a partir de un valor de su coordenada radial muy grande respecto del radio de Schwarzschild de un agujero negro (que no rota), emplea un intervalo finito de tiempo propio en alcanzar el horizonte de eventos del agujero negro, situado en r = rS . No obstante, la duración de la caída hasta el horizonte de eventos del agujero negro, medida en términos de tiempo inercial, es infinita.
Esto se desprende de las fórmulas para
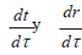 obtenidas en el Apéndice D. De estas fórmulas se desprende, para rS < r ≤ r
0:
obtenidas en el Apéndice D. De estas fórmulas se desprende, para rS < r ≤ r
0:
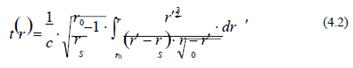
Cuando la coordenada radial se aproxima a r
S
la integral diverge
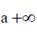
Entonces, como la coordenada temporal t (r ) corresponde al tiempo para el cual la partí- cula se encuentra a una distancia r del centro del agujero negro, tal como lo determina un observador inercial muy alejado y respecto del cual la masa del agujero negro se halla en reposo, para este observador inercial el tiempo de aproximación de la partícula (tiempo inercial) desde r =r0 hasta el horizonte de eventos ( r = rS )es infinito.
Una consecuencia de esta doble descripción, en un caso por un observador alejado y en reposo respecto del agujero, y en el otro caso por un observador en co-movimiento con la materia atraída hacia el agujero, es la imposibilidad de asignar un valor del tiempo t en el que ocurren los eventos que determina el primer observador, para cada valor que puede tomar el tiempo propio, en el que ocurren de los eventos que determina el segundo observador.
5.-DISCUSIÓN Y CONCLUSIONES
Todo el análisis anterior sobre la relación entre el tiempo propio y el tiempo inercial se basa en la validez de la hipótesis del reloj y en el concepto de reloj ideal. Se supone que el ritmo de un reloj ideal acelerado es igual al ritmo de un reloj no acelerado en co- movimiento con el reloj acelerado, independientemente de la historia de velocidad del reloj con respecto a un sistema inercial de referencia. Por lo tanto, no se introducen limitaciones en las aceleraciones propias permisibles. Sin embargo, algunos trabajos recientes, ya sea de reinterpretación de experimentos conocidos10,11) o bien desarrollos teóricos12,13, sugieren la posible existencia de aceleraciones máximas. Si esto es correcto, en el marco de la relatividad especial, la hipótesis del reloj sería solo una aproximación a una relación más general.
En ausencia de efectos gravitatorios, y en el marco de la relatividad especial, un reloj fijo a un sistema de inercia y aislado de las acciones externas, si se construye correctamente, podría considerarse un reloj ideal. Después de acelerar, uno esperaría que se comportara tanto más cercano de un reloj ideal cuanto menor sea la relación entre la magnitud de las fuerzas externas asociadas con la aceleración y la magnitud de las fuerzas de cohesión internas asociadas con la integridad de la estructura material del reloj.
La hipótesis del reloj se confirmó para las vidas medias de muones positivos y negativos almacenados en una órbita circular con aceleraciones transversales, y para las vidas me- dias de los bariones Sigma con aceleraciones longitudinales14,16.
La concordancia observada entre las vidas medias de las partículas aceleradas y la del mismo tipo de partículas, con la misma energía, moviéndose inercialmente, confirma la hipótesis del reloj para aceleraciones de casi 1019 m / s2 en el primer caso y casi 1016 m / s2 en el segundo caso.
Para concluir con lo que se refiere a la convergencia de la integral del tiempo propio en el marco de la teoría restringida de la relatividad:
Nada especial parece caracterizar el comportamiento de la componente tangencial de los campos de 3-fuerzas, a lo largo de la trayectoria del reloj acelerado y respecto de un mar- co inercial, en relación con la convergencia o divergencia de la integral que da el tiempo propio como función del tiempo inercial. Las historias fronterizas de 3-fuerza tangencial que dan convergencia en un caso o divergencia en otro, involucran fuerzas crecientes en ambos casos, la única diferencia aparece en el orden de crecimiento al infinito.
Sin embargo, vista desde el punto de vista de la aceleración propia del reloj, aparece una diferencia físicamente significativa entre: (a) las historias de aceleración propia tangencial (y las historias de 3-fuerza propia relativista tangencial) que dan un tiempo propio finito para un tiempo inercial infinito y (b) aquellas historias de 3- aceleraciones tangenciales propias (y sus historias de 3-fuerzas relativistas propias tangenciales ) que dan un tiempo propio infinito por un tiempo inercial infinito. Ya sea una singularidad en la 3- aceleración propia (y en la 3-fuerza propia) para un valor finito del tiempo propio en un caso, o su ausencia en el otro caso.
Si admitimos que las aceleraciones propias no pueden tener singularidades en la trayectoria del reloj acelerado, se puede excluir el caso del tiempo propio finito para un tiempo de inercia infinito, y se resuelve el problema que motiva este trabajo.
Con referencia a lo que acontece con el tiempo propio durante la caída hacia un agujero negro, en el marco de la teoría de la relatividad generalizada:
Según un observador inercial, un observador acelerado que cae libremente hacia un aguje- ro negro, nunca cruza el horizonte de eventos del agujero negro.
Para el observador que cae, el evento de cruce acontece para un valor finito de su tiempo propio. Los tiempos propios más allá de ese punto nunca son accesibles para el observa- dor inercial externo si suponemos que el tiempo no tiene fin: parte de la experiencia del observador acelerado respecto del observador fijo a un marco inercial, se desarrolla para valores de tiempo (tiempo propio del reloj acelerado) que no tienen equivalente en la experiencia del observador inercial.
Entonces parte de la evolución del universo del observador no inercial debe ocurrir fuera del universo del observador inercial, porque el tiempo de este último literalmente se agotó.
Este tipo de situación entra en contradicción con el principio según el cual la equivalencia entre todos los posibles sistemas de referencia para describir el mundo físico debería implicar que existe una correspondencia entre los instantes que dos observadores atribu- yen al mismo evento, tal que a cada instante determinado por uno de ellos le corresponda un único instante determinado por el otro para el mismo evento.
Es decir, los eventos que acontezcan en la experiencia finita de un observador también deben acontecer en la experiencia finita de otro observador: unus mundus, hay un solo mundo (físico).
Evidentemente las consecuencias de los modelos relativistas más aceptados para describir los agujeros negros implican que no se cumple el principio mencionado: no hay un solo mundo físico en el sentido que le hemos dado a esta expresión.
Para el observador que se está acelerando, el observador inercial desaparecerá detrás de un horizonte. Como se menciona en el Apéndice B, sección (B.2), esto ocurre ya para el caso de un observador con aceleración propia constante. Si la aceleración es constante la integral del tiempo propio diverge cuando el tiempo inercial tiende a infinito, y no apare- ce el problema que motiva este trabajo.
Pero como se muestra en el Apéndice B, sección (B.1), si la aceleración aumenta lo suficiente con el tiempo, la integral del tiempo propio converge cuando el tiempo inercial tiende a infinito. Entonces, desde el punto de vista del observador inercial, la dilatación del tiempo del reloj acelerado será tan fuerte que el observador que viaja con el reloj acelerado nunca alcanzará el correspondiente valor límite del tiempo propio. Desde el punto de vista del observador acelerado se puede exceder el tiempo propio crítico, pero el observador inercial habrá desaparecido detrás de un horizonte, ubicado en sentido opuesto al de la aceleración. Para el observador inercial, el horizonte detrás del cual desaparece el observador acelerado está en el infinito. Por lo tanto, para los tiempos propios más allá del valor límite, el observador acelerado debe estar, de hecho, fuera del universo del observador inercial. Pero lo dejó en la dirección del tiempo, por así decirlo. Moviéndose hasta casi alcanzar la velocidad de la luz, él también está a una distancia infinita.
En suma, en el marco de la teoría restringida de la relatividad, un observador con suficiente energía como para lograr una historia de velocidad adecuada podría recorrer una distancia infinita en un tiempo propio finito.
En el marco de la teoría generalizada de la relatividad, un observador que cae en un agujero negro a partir del reposo (respecto de un observador ubicado en un sistema inercial) recorre una distancia finita demorando un tiempo infinito desde el punto de vista del observador inercial. No obstante el observador acelerado hacia el agujero negro recorre esa distancia en un tiempo propio finito.
APÉNDICE A: POSTULADO DEL RELOJ Y PARADOJA DE LOS GEMELOS.
Consideremos dos relojes ideales. Un primer reloj está fijo a un sistema de referencia inercial. El tiempo inercial, dado por este reloj, se representa por t .
Un segundo reloj, hasta el instante ti se encuentra también en reposo adyacente al primer reloj y sincronizado con él.
Desde el instante ti en adelante, el segundo reloj se aparta del primero y viaja siguiendo una trayectoria
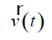 respecto al sistema inercial.
respecto al sistema inercial.
En un instante posterior tf el segundo reloj encuentra nuevamente al primero y se detiene adyacente a él.
Siendo la trayectoria cerrada, las posibles historias de velocidad
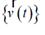 verifican la restricción:
verifican la restricción:
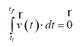 referencia inercial es tf ( ti . El tiempo transcurrido entre esos mismos eventos, medido por el reloj acelerado, siendo
referencia inercial es tf ( ti . El tiempo transcurrido entre esos mismos eventos, medido por el reloj acelerado, siendo
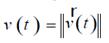 la historia de rapidez correspondiente a la historia de velocidad v (t ), de acuerdo con la hipótesis del reloj es
la historia de rapidez correspondiente a la historia de velocidad v (t ), de acuerdo con la hipótesis del reloj es
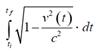 Este intervalo de tiempo es siempre menor que el intervalo medido por el reloj inercial. Si se asume que el tiempo propio es también la medida del tiempo más conveniente para medir procesos biológicos, esta es la denominada y bien conocida “paradoja de los gemelos”. Queda claro que la posible convergencia de la integral
Este intervalo de tiempo es siempre menor que el intervalo medido por el reloj inercial. Si se asume que el tiempo propio es también la medida del tiempo más conveniente para medir procesos biológicos, esta es la denominada y bien conocida “paradoja de los gemelos”. Queda claro que la posible convergencia de la integral
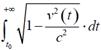 es otra cosa, aunque esa convergencia presupone la dilatación del tiempo de los relojes acelera- dos.
es otra cosa, aunque esa convergencia presupone la dilatación del tiempo de los relojes acelera- dos.
Apéndice B: dos historias de rapidez sobre la trayectoria de un reloj acelerado.
(B.1) Primer ejemplo de una historia de rapidez a la que corresponde un tiempo propio finito para un tiempo inercial infinito.
Consideremos la siguiente historia de rapidez sobre la trayectoria del reloj:
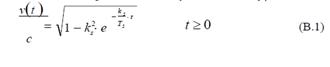
Teniendo en cuenta la igualdad (3.5), respecto al marco de referencia inercial la componente tangencial de la 3-fuerza relativista viene dada por:
Así pues, un cuerpo que se deja caer desde el reposo, a partir de un valor de su coordenada radial muy grande respecto del radio de Schwarzschild de un agujero negro que no rota, emplea un intervalo finito de tiempo propio en alcanzar la singularidad situada en el origen de coordenadas2,3.











 uBio
uBio