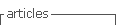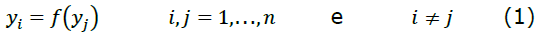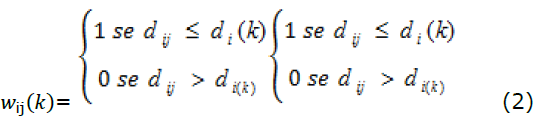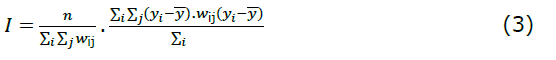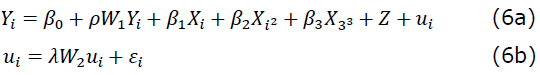INTRODUÇÃO
De acordo com Viola e Leis (1992), durante a Conferência das Nações Unidas sobre Desenvolvimento e Meio Ambiente (CNUMAD), também conhecida como ECO-92, Rio-92, documentou-se que a percepção sobre os problemas do sistema econômico vigente cresceu, fato que promoveu e ampliou a discussão entre as relações do desenvolvimento socioeconômico e das transformações ecológicas.
Nesse contexto, Stern & Common (2001) investigaram uma relação que passaria a ser chamada de Curva de Kuznets Ambiental (CKA), aceitando-se que algumas medidas de degradação ambiental aumentariam nos primeiros momentos do crescimento econômico, no entanto, ao alcançar certo nível de renda, eventualmente, a degradação diminuiria.
Segundo Fonseca e Ribeiro (2004), um “efeito renda” prevalece, resultando no fato de a qualidade ambiental, nessa análise considerada como um bem, e este ser um bem de luxo, pois, no início do crescimento econômico, os indivíduos optam pelo emprego e liquidez, e poucos estão dispostos a preferir investimentos em proteção ambiental, o que piora os fatores ambientais. Mas, quando esses indivíduos atingem um determinado nível de renda, passam a dar preferência pela qualidade de vida, acarretando uma demanda maior pela “bem” qualidade ambiental. Assim, ocorre uma melhora dos indicadores ambientais, e isso implica que o impacto ambiental seja uma função na forma de “U” invertido na renda per capita.
O conceito de que os impactos ambientais primeiro aumentam e depois decrescem com o crescimento da renda se fortaleceu em convicções preexistentes de que países em desenvolvimento são considerados “muito pobres para serem verdes”, ou seja, só a partir do momento em que é atingido certo nível de desenvolvimento, os impactos diminuem (Carvalho e Almeida, 2010). Beckerman (1992) acredita que exista uma evidência clara de que, embora o crescimento econômico normalmente leve à degradação ambiental nos estágios iniciais do processo, no fim, o melhor, o único caminho para se obter um meio ambiente decente é se tornar mais rico.
Quando o crescimento ocorre em um país pobre, a degradação ambiental cresce num primeiro momento porque os aumentos na produção geram emissões de poluentes e o país coloca uma baixa prioridade para o controle da degradação ambiental; e uma vez que o país ganha suficiente grau de afluência, sua prioridade muda, passa a ser a proteção da qualidade ambiental, causando o declínio da degradação ambiental, podendo a melhoria ambiental somente ser alcançada com o crescimento econômico (Deacon & Norman, 2004).
Bruyn et al. (1998) afirmaram que a Curva de Kuznets Ambiental não se sustenta no longo prazo, e o formato de “U” invertido seria apenas um estágio inicial, pois, após certo nível de renda, um novo ponto de inflexão surgiria, tornaria a trajetória ascendente novamente, e o formato da curva seria similar ao de um “N”, sugerindo que a degradação ambiental voltaria a aumentar em altos níveis de crescimento. Já Stokey (1998) defende a hipótese de que a relação entre renda e degradação ambiental ocorre num ponto limite, a partir do qual somente tecnologias “limpas” são usadas, mostrando o formato da Curva de Kuznets Ambiental como V-invertido, sendo o ápice tal ponto limite.
O estado de Mato Grosso do Sul, localizado na região Centro-Oeste do Brasil, contribuiu, em 2008, com 1,1% para o Produto Interno Bruto (PIB) brasileiro. No âmbito regional, sua participação foi de 11,9%, sendo a menor entre as unidades federativas do Centro-Oeste, entretanto, o estado vem apresentando o maior crescimento econômico da região. A agropecuária é um elemento de fundamental importância para a economia estadual, uma vez que em 80,76% das cidades o PIB do Agronegócio per capita é maior do que o PIB per capita da indústria, além de impulsionar o setor industrial e de serviços no estado (Secretaria de Estado de Meio Ambiente, do Planejamento, da Ciência e Tecnologia [SEMAC], 2015).
São grandes os impactos ambientais que o estado de Mato Grosso do Sul vem sofrendo. O estado desmatou, entre 2009 e 2010, 310,36 km² do Bioma Cerrado, enquanto o PIB foi de R$ 43,5 bilhões, crescendo 11% no ano de 2010 (Ministério do Meio Ambiente do Brasil [MMA], 2015). A área desmatada de Mata Atlântica aumentou em 10,49% entre 2012 e 2013 (SOS Mata Atlântica [SOSMA], 2015), enquanto a previsão para o crescimento do PIB foi de 3,77%, equivalendo a R$52,9 bilhões em 2013 (SEMAC, 2015).
Para Santos, Diniz, Diniz, Rivero e Oliveira (2008), uma das principais causas do desmatamento no Brasil é a atividade agropecuária, que foi altamente favorecida por políticas públicas, através do fornecimento de créditos. Os autores destacam ainda a ausência ou a ineficácia da fiscalização ambiental. Culas (2007) destaca exatamente estes pontos - instituições fracas e políticas públicas ineficientes - para a preservação das florestas em seu estudo comparando países da América Latina.
Uma vez que Kuznets (1955) considera que com o crescimento econômico (PIB) os impactos ambientais tendem a ser menores, devido ao fato de maior preocupação com o meio ambiente e, assim, maior proteção contra degradações, a hipótese que norteia o presente artigo é que a Curva de Kuznets Ambiental de Mato Grosso do Sul se apresente em sua maneira clássica, a de “U” invertido, significando que um crescimento econômico significaria uma melhora nos indicadores ambientais.
O presente artigo tem por objetivo indagar a hipótese da curva de Kuznets Ambiental para os municípios de estado de Mato Grosso do Sul, para o ano de 2008, buscando identificar a relação entre degradação ambiental (desmatamento) e crescimento econômico.
A principal contribuição da presente pesquisa está em estimar a curva de Kuznets Ambiental para o estado de Mato Grosso do Sul, que tem na agricultura sua principal força e apresenta em seu território três biomas - Pantanal, Mata Atlântica e Cerrado - enriquecendo a literatura sobre o tema para diferentes biomas. A discussão sobre a Curva de Kuznets Ambiental é importante porque é do aprofundamento desta discussão que se define a necessidade ou não de política pública, tendo em vista corrigir os danos ambientais causados pelo crescimento econômico.
REFERENCIAL TEÓRICO
Desenvolvimento sustentável
Sempre existe um risco de que o crescimento econômico prejudique de alguma forma o meio ambiente, uma vez que tal crescimento aumenta a pressão sobre os recursos ambientais. No entanto, os estudiosos que se orientam pelo conceito de desenvolvimento sustentável deverão garantir que, mesmo com o crescimento econômico, os países possam continuar ligados a suas raízes ecológicas, sustentando-as a longo prazo, dando apoio ao crescimento (Brundtland, 1991).
Para Lélé (1991), se o desenvolvimento sustentável é para ser realmente “sustentado” como um paradigma de desenvolvimento, deve-se atentar para dois esforços, aparentemente divergentes, fazendo com que o conceito seja mais preciso em suas bases, ou seja, permitir maior flexibilidade e diversidade de abordagens para que possam ser desenvolvidas estratégias que permitam à sociedade viver em harmonia com ela mesma e com o meio ambiente.
É consenso no Relatório de Brundtland (1991) que, para haver desenvolvimento sustentável, é necessária a minimização dos impactos, tratando-se de um processo de transformação no qual a exploração dos recursos, a direção dos investimentos, a orientação do desenvolvimento tecnológico e a mudança institucional reforçam o potencial presente e futuro, para atender às necessidades e aspirações humanas, tendo como objetivos: retomar o crescimento, alterar a qualidade do desenvolvimento, atender às necessidades de emprego, alimentação, energia, água e saneamento, manter um nível populacional sustentável, conservar e melhorar a base de recursos, reorientar a tecnologia e administrar o risco e incluir o meio ambiente e a economia no processo de tomada de decisões.
O desenvolvimento sustentável sofre com o fato de muitas pessoas pensarem erroneamente que a conservação ambiental necessariamente restringe o desenvolvimento ou que o desenvolvimento necessariamente significa poluição ambiental. Devido aos erros de interpretação dos conceitos e objetivos, as políticas de desenvolvimento sustentável adotadas, muitas vezes, não trazem a ideia básica, que é um desenvolvimento ecologicamente correto e socialmente justo, refletindo muitas vezes preferências pessoais, organizacionais e políticas (Lélé, 1991).
Hart e Milstein (2004) acreditaram que, mesmo com a disseminação do conceito da sustentabilidade, ainda se considera que o desenvolvimento sustentável seja uma espécie de “mal necessário”, no entanto, a sustentabilidade não é irreconciliável com o crescimento econômico, mas pode ser uma fonte de vantagem competitiva e de geração de valor. As tecnologias limpas não se referem a melhorias incrementais associadas ao combate à poluição, mas às inovações que ultrapassam as rotinas e o conhecimento comum, à rápida emergência de tecnologias revolucionárias, representando a oportunidade de as empresas reposicionarem suas competências internas em torno de tecnologias mais sustentáveis.
Em vez de apenas buscar reduzir os impactos negativos de suas operações, empresas sustentáveis têm por objetivo solucionar problemas sociais e ambientais por meio do desenvolvimento econômico, ou pela aquisição de novas capacitações com o objetivo de solucionar os desafios da sustentabilidade. As competências sustentáveis que se originam da busca por tecnologias limpas são centrais nos esforços para reposicionar o conjunto de habilidades para o desenvolvimento e exploração de mercados futuros (Hart e Milstein, 2004).
Barreto e Vilaça (2018) consideram que a educação sustentável a muito tempo vem se tornando importante, sendo que é importante o conhecimento sobre conceitos e tendências nacionais e internacionais. Os autores consideram ainda que grande parte dos problemas ambientais globais se relacionam com estilos de vida e condição de vida local, assim, existe a necessidade de pensar a educação, com ações que englobam a aprendizagem através de metodologias desenvolvidas no sentido de promover o desenvolvimento da competência para ação ambiental.
De Avelar Teixeira e Costa (2018) defendem que a questão ambiental é extremamente afetada por: problema econômico, sustentabilidade e desenvolvimento da atividade econômica, visto que as explorações de recursos naturais levam à conflitos relacionados com uma nova ordem de proteção ambiental. Para os autores é relevante compreender a necessidade de uma economia pautada na sustentabilidade e na internalização da externalidade, e ainda consideram imprescindível a submissão dos interesses econômicos individuais a um desenvolvimento sustentável de forma coletiva, distributiva e o resguardo desses em mecanismos legais e legítimos, criando uma nova ordem econômica.
A Curva de Kuznets Ambiental
Em Economic Growth and Income Inequality (1955), Simon Kuznets, utilizando um modelo dual com um setor moderno e dinâmico e outro agrícola, buscando analisar a relação entre desigualdade e o crescimento econômico, supôs que a desigualdade se elevaria em um primeiro momento e, com o crescimento econômico, reduziria, formando assim um “U” invertido da relação entre crescimento econômico e pressão ambiental.
Para Fields (2002), o que está por trás da hipótese de Kuznets é o fato de o crescimento econômico gerar uma realocação gradual das atividades econômicas, iniciando em estágio em que há uma baixa desigualdade, quando o país ainda possui atividades econômicas consideradas tradicionais, dirigindo-se para uma desigualdade alta quando atinge uma economia moderna, com renda média, voltando a apresentar uma baixa desigualdade quando atinge um estado avançado de desenvolvimento.
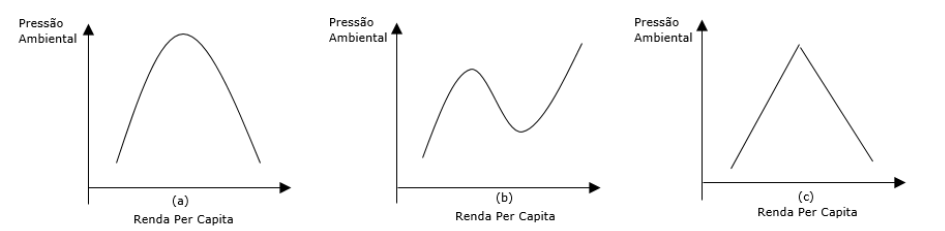
As interpretações a respeito da Curva de Kuznets Ambiental podem variar de acordo com a bibliografia adotada, ocorrendo diferença entre a interpretação de alguns autores. A Figura 1 mostra as tipologias conhecidas da CKA, em forma de “U” invertido (a), “V” invertido (b) e, por fim, no formato de “N”(c).
Um dos primeiros estudos empíricos com o objetivo de testar e confirmar a hipótese da Curva de Kuznets Ambiental foi desenvolvido por Grossman e Krueger (1993), que analisaram a relação entre a poluição do ar e a renda; em seguida, outros estudiosos como Selden & Song (1994), Shafik (1994), Cole, Rayner & Bates (1997), Hilton & Levinson (1998) e Arraes, Diniz e Diniz (2006) testaram a hipótese da Curva de Kuznets Ambiental, com explicações diversificadas para explicar o fenômeno.
Arraes et al. (2006) utilizaram um modelo cúbico para testar a hipótese da curva de Kuznets para indicadores de meio ambiente e desenvolvimento sustentável. Anand & Kanbur (1993) e Barros e Gomes (2007) utilizaram como medida o índice de Gini e L de Theil para analisar se a hipótese de Kuznets é verdadeira, sendo que Anand & Kahbur (1993) rejeitaram a hipótese.
Assim como Anand & Kahbur (1993), Harbaugh, Levinson & Wilson (2000) refutaram a hipótese da Curva de Kuznets Ambiental, sendo que o maior problema está na tentativa de explicar a fase descendente da CKA, principalmente se o que está em estudo são economias em desenvolvimento. Para Santos et al. (2008), isso também poderia ter relação com a própria transição da agricultura para patamares mais modernos, quando o setor industrial passaria a exigir mais da própria agricultura, aumentando, assim, a correlação entre crescimento econômico e pressão ambiental.
METODOLOGIA
Econometria espacial
A aplicação das técnicas de econometria espacial é aconselhada sempre que se trabalha com dados espaciais em que as chances de implicações como a dependência espacial e a heterogeneidade espacial sejam altas. Os dados espaciais denotam a variação de algum fenômeno, com a preocupação de saber onde ocorre tal variação (Fotheringham, Brunsdon & Charlton, 2000). Já os dados considerados não espaciais são aqueles que apenas registram a variação sem se preocupar em determinar onde tal variação ocorreu (Almeida, 2010).
Indicadores de autocorrelação espacial
A existência de autocorrelação espacial indica que o valor de uma variável de interesse em uma certa região i depende do valor da mesma variável nas regiões vizinhas j (Almeida, 2010):
Uma matriz de ponderação espacial (W) é uma matriz de dimensão nxn, em que N é o número de observações de natureza não estocástica. Os pesos espaciais w ij e apresentam a influência da região j sobre a região i. Portanto, a matriz W é útil por fazer uma ponderação da influência que as regiões exercem umas sobre as outras.
A matriz de peso espacial adotada no presente artigo será a de distância geográfica, uma matriz embasada em k vizinhos mais próximos, 𝑤 ij 𝑘 , uma matriz binária:
em que 𝑑 𝑖 𝑘 é a distância de corte para a região i, especificamente, para que nessa região haja k vizinhos, sendo essa região a menor região possível para a região i.
A variável k é definida de acordo com o procedimento de Baumont (2004) apud (Almeida, 2010) para tornar menos arbitrária essa decisão:
Primeiramente, rodamos o MQO; testamos os resíduos para autocorrelação espacial com base na estatística I de Moran, usando N matrizes de k vizinhos mais próximos (variando n de k=1 a k=20); e finalmente, define-se k que tenha gerado o maior valor do I de Moran.
Uma vez calculada a matriz W, podemos implementar os indicadores de grau de correlação espacial:
- I de Moran:
A estatística de autocorrelação espacial I de Moran (1948) é descrita da seguinte forma:
em que n é o número de regiões, 𝑦 𝑖 é a variável dependente, 𝑦 é a média de y e 𝑤 ij refere-se ao elemento da matriz de pesos espaciais.
Valores de I de Moran que excedem −indicam autocorrelação espacial positiva, e abaixo disso, sinalizam autocorrelação negativa. Um sinal positivo indica que, no geral, altos valores de uma variável de interesse tendem a estar circundados por altos valores dessa variável em regiões vizinhas, ou ao contrário. Um valor de I negativo indica dissimilaridade entre os valores, um alto valor da variável de interesse tende a ser rodeado por baixos valores da mesma variável nas regiões vizinhas.
- G de Getis-Ord:
A estatística proposta por Getis e Odis (1992) é:
em que 𝑦 𝑖 é o valor observado de uma variável na região i e 𝑤 ij é o elemento da matriz de pesos espaciais. Diferentemente do I de Moran, o G de Getis-Ord não é definido na forma de desvios da média.
Um valor de G positivo significa que uma região com elevado valor para a variável y é rodeada por regiões que também tenham um elevado valor para a variável, caso contrário, indica que uma região com baixo valor é circunvizinha de regiões com baixos valores.
Respaldado somente nesses resultados exploratórios, não é possível verificar a hipótese da CKA. É necessário ir adiante em direção à abordagem econométrica para que se encontre a trajetória no tempo que o desmatamento do bioma cerrado segue em decorrência do crescimento econômico, assim como encontrar a influência de outras variáveis no desmatamento.
Modelo de defasagem espacial
O efeito de defasagem espacial é ocasionado pela dependência espacial criada por uma interação espacial entre variáveis. Neste caso, esta influência é medida pela inclusão de uma variável adicional no modelo, dada por Wy, em que um provável efeito de vizinhança, por exemplo, o desmatamento em uma determinada região, provoca efeitos em seus vizinhos. Desta forma, o modelo então será expresso da seguinte forma:
em que que y é um vetor nx1 de observações sobre a variável dependente; Wy é o vetor nx1 da defasagem espacial para a variável dependente; ρ é o coeficiente autorregressivo espacial (um escalar); X é uma matriz nxk de observações sobre as variáveis explicativas exógenas (mais a constante) com um setor associado kx1 de coeficientes de regressão β; e ε é um vetor nx1 de termos de erro aleatório distribuído, idêntica e independentemente, com média zero e variância constante.
De acordo com Teixeira e Bertella (2010) e Anselin (1988), o fato de não considerar a defasagem espacial neste modelo levaria a um problema semelhante ao de omissão de variável relevante, isto é, os coeficientes estimados por MQO das variáveis explicativas seriam tendenciosos.
Modelo de erro espacial
Segundo Dantas, Magalhães e Vergolino (2001), o modelo de erro espacial é apropriado quando as variáveis não incluídas no modelo e presentes nos termos de erro, sendo espacialmente autocorrelacionadas. Desse modo, a dependência espacial pode ser decorrente de efeitos não modelados que não foram aleatoriamente distribuídos através do espaço.
A utilização de MQO na presença de erros não esféricos, segundo Teixeira e Bertella (2010), geraria estimativas ineficientes, apesar de justas. Diante dessa situação, é aconselhável estimar o modelo de erro espacial pelo método de máxima-verossimilhança (MV) ou pelo Método Generalizado dos Momentos (GMM).
O modelo estimado
O procedimento utilizado teve como base Anselin (1988), Folmer e Rey (2003) e Teixeira e Bertella (2010), consistindo do seguinte procedimento:
1) Estimar o modelo de regressão linear por MQO;
2) Testar a hipótese de ausência de autocorrelação;
3) Se for constatado que não existe autocorrelação, deve-se utilizar o modelo clássico; e
4) Se ambos os testes forem significativos, devem ser verificadas as versões robustas de ambos. Caso contrário, adota-se o modelo de erro espacial, pelo Método Generalizado dos Momentos (GMM).
Esta análise se limitou a examinar se existe dependência espacial para uma Curva de Kuznets Ambiental em Mato Grosso do Sul, segundo dados para o ano de 2008. O modelo empírico econométrico apresenta a seguinte forma:
em que Yi é a variável dependente; 𝛽 0 é a constante = 0 (Arraes et al., 2006); W 1 Y i é a defasagem espacial da variável dependente;
são as variáveis independentes, que explicam a variável dependente; W 2 u i é a defasagem do termo de erro; e W1 e W2 são matrizes de pesos espaciais, que tentam capturar a estrutura de dependência espacial. As demais letras gregas são parâmetros a serem estimados. A média do termo de erro εi é zero .As variáveis do modelo são apresentadas na Tabela 1.
Tabela 1 Estatística descritiva das variáveis estudadas.

*Desmatamento per capita ** Produto Interno Bruto per capita *** Produto Interno Bruto do Agronegócio per capita.
Fonte: Resultados da pesquisa.
Os parâmetros β1, β2 e β3 mostraram a forma da Curva de Kuznets Ambiental de Mato Grosso do Sul, sendo que, para que a hipótese CKA na forma de um “U” invertido seja válida, o coeficiente β1 precisa ser positivo e significativo, ao passo que o coeficiente estimado β2 precisa ter o sinal negativo e significativo e o coeficiente β3 não ser significativamente diferente de zero. Se β3 for significativo e tiver sinal positivo, isso mostraria evidências de que a CKA tem forma de “N.
Variáveis do modelo estimado para a CKA de Mato Grosso do Sul:
Yi: Logaritmo natural do desmatamento per capita do município i.
Xi: Logaritmo natural do produto interno bruto per capita do município i.
Xi 2: Logaritmo natural do produto interno bruto per capita do município i elevado ao quadrado.
Xi 3: Logaritmo natural do produto interno bruto per capita do município i elevado ao cubo.
Zi: Logaritmo natural do produto interno bruto do agronegócio per capita do município i.
O desmatamento per capita é o desmatamento total do município dividido pela sua população. O PIB per capita é a razão entre o PIB total do município e sua população total. A variável Xi, elevada ao quadrado e ao cubo, é para simular o crescimento econômico ao longo do tempo. A variável PIB do agronegócio foi incorporada ao modelo, uma vez que estamos tratando de desmatamento, logo, pode haver relação direta com o crescimento econômico do agronegócio, visando, assim, a aumentar o grau de confiança do modelo.
Base de Dados
Os dados referentes ao desmatamento para o Cerrado foram obtidos na base de dados da SEMAC (Secretaria de Estado de Meio Ambiente, do Planejamento, de Ciência e Tecnologia, 2015) de Mato Grosso do Sul e no Relatório de Monitoramento do Desmatamento nos Biomas Brasileiros por Satélite (Bioma Cerrado de 2002 a 2008) do Centro de Sensoriamento Remoto do IBAMA (CSR/IBAMA, 2015), de novembro de 2009.
Os dados referentes ao desmatamento do bioma Pantanal foram obtidos no Relatório de Monitoramento do Desmatamento nos Biomas Brasileiros por Satélite (Bioma Pantanal de 2002 a 2008) Centro de Sensoriamento Remoto do IBAMA (CSR/IBAMA, 2015), de maio de 2010.
Os dados referentes ao desmatamento do bioma Mata Atlântica foram obtidos no Relatório de Monitoramento do Desmatamento nos Biomas Brasileiros por Satélite (Bioma Mata Atlântica de 2002 a 2008) do Centro de Sensoriamento Remoto do IBAMA (CSR/IBAMA, 2015), de novembro de 2010.
O Produto Interno Bruto das cidades e o Produto Interno Bruto do Agronegócio foram obtidos na base de dados da SEMAC (Secretaria de Estado e Meio Ambiente, do Planejamento, de Ciência e Tecnologia) de Mato Grosso do Sul, sendo os dados referentes ao ano de 2008. A utilização de dados só até 2008, se dá pelo feito do segundo o Instituto Brasileiro de Geografia e Estatística (IBGE) no 2008, em Mato Grosso do Sul 88,4% dos municípios registraram ocorrências que causaram impactos ambientais muito relevantes no último 24 meses. Dado esses dados foi escolhida esse ano para trabalhar.
RESULTADO E DISCUSSÕES
O estado de Mato Grosso do Sul tem três biomas: Pantanal, Cerrado e Mata Atlântica. O maior bioma é o do Cerrado, que ocupa 61% do total do território do estado; o segundo maior é do Pantanal, com 25% do território; e com uma menor área, compreendendo 14% do total do estado, a Mata Atlântica.
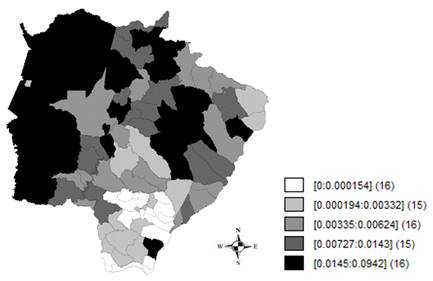
A área média desmatada per capita das cidades de Mato Grosso do Sul foi de 0,0095284 km² e a média do PIB de R$ 13.150,97. A seguinte figura mostra o desmatamento nas cidades do estado.
Foi observado que, predominantemente, as regiões Cone Sul e Sul-fronteira não apresentaram desmatamento muito elevado, o que pode ser explicado pelo fato de que na região já ocorrer desmatamento consolidado, ou seja, a tendência é que, com o passar dos anos, e em virtude da área de Mata Atlântica (bioma predominante na região) já desmatada e da área protegida, os dados do desmatamento sejam menores.
Com desmatamento de 0 km² a 0,000154 km² per capita, aparecem 16 cidades, onde é predominante o bioma Mata Atlântica. Observa-se desmatamento de 0,000194 km² a 0,00332 km² per capita em 15 cidades, tendo 21 cidades apresentado desmatamento de 0,00335 km² a 0,0143 km² per capita, na região mais central e nordeste do mapa, onde o bioma Cerrado é predominante, além de uma pequena parcela do Pantanal, ao norte do mapa. As maiores áreas de desmatamento da amostra são de 16 cidades, iniciando com 0,0145 km², e o maior desmatamento da amostra foi de 0,0942 km² per capita, essa área engloba predominantemente as regiões de fronteira com Bolívia e Paraguai, com os biomas Cerrado e Pantanal, além da região central (bolsão e região de Campo Grande) (Figura 2).
A estatística I de Moran fornece uma indicação do grau de autocorrelação espacial. O valor da estatística I de Moran foi de 0.29669, com um p-valor de 0.001, conforme o diagrama da Figura 3.
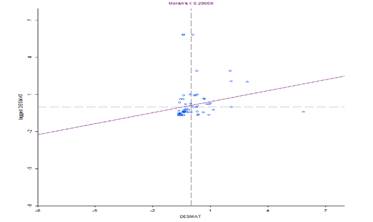
Figura 3. Diagrama I de Moran - grau de autocorrelação espacial do desmatamento em Mato Grosso do Sul.
Uma vez que o valor da estatística I de Moran foi maior que -[1/ (n-1) ], considera-se que no estado de Mato Grosso do Sul há uma autocorrelação espacial positiva para os dados de desmatamento per capita. O fato de o sinal ser positivo deixa implícito que cidades com um alto (baixo) desmatamento per capita tendem a ser circundadas por cidades com o mesmo nível de desmatamento. Observa-se presença de cidades “outliers”, que se distanciam da reta e dos clusters. A inclinação da reta reafirma uma autocorrelação espacial positiva.
Nota-se claramente a existência de dois clusters predominantes: o Baixo-Baixo, apresentado no terceiro quadrante do diagrama, referindo-se a um grupo de associações espaciais cujas regiões apresentam valores abaixo da média, circundados por regiões que contemplam os valores também abaixo da média, e o cluster Alto-Alto, que representa aquelas regiões que têm o desmatamento acima da média e são rodeadas pelas demais regiões com o índice da variável de interesse também acima da média.
A Figura 4 do lado esquerdo mostra os clusters espaciais de I de Morgan para o desmatamento nas cidades de Mato Grosso do Sul, definindo os clusters em Alto-Alto (AA), Alto-Baixo (AB), Baixo-Baixo (BB) e Baixo-Alto (BA).
O cluster Alto-Alto é formado pelas cidades de Alcinópolis, Anastácio, Camapuã, Figueirão e Porto Murtinho; o cluster Baixo-Baixo, pelas cidades de Eldorado, Fátima do Sul, Glória de Dourados, Iguatemi, Japorã, Jateí, Juti e Rio Brilhante; já o cluster Baixo-Alto, pelas cidades de Sidrolândia e Terenos.
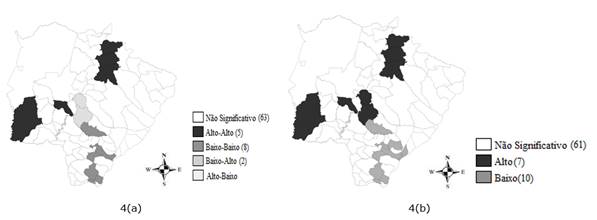
Figura 4. Mapa de cluster de I de Moran - 4(a) e mapa de cluster da estatística G de Getis-Ord - 4(b).
A estatística G em média foi de 0,01593, com grau de significância de 0,05. Tal resultado indica que cidades com alto (baixo) índice de desmatamento em Mato Grosso do Sul tendem a ser rodeadas por cidades com alto (baixo) índice de desmatamento, ou seja, podemos rejeitar a hipótese de distribuição aleatória do desmatamento em Mato Grosso do Sul, O mapa de clusters da estatística G pode ser visto na Figura 4b.
O cluster alto é formado pelas cidades de Porto Murtinho, Sidrolândia, Terenos Figueirão, Camapuã, Anastácio e Alcionópolis, enquanto o cluster Baixo é formado pelas cidades de Eldorado, Fátima do Sul, Glória de Dourados, Iguatemi Ivinhema, Japorã, Jateí, Juti, Rio Brilhante e Taquarussu, e as outras sessenta e uma cidades foram consideradas não significativas.
É necessário ir adiante em direção à abordagem econométrica para encontrar a trajetória no tempo que a quantidade de desmatamento segue em decorrência do crescimento econômico. Em relação à análise econométrica, inicialmente, estimou-se uma regressão contra o PIB per capita, seu valor ao quadrado e as outras variáveis explanatórias pelo método MQO, sem considerar a correção espacial.
Optou-se por rodar dois modelos. O modelo 1 é um modelo cúbico, com ln do PIB per capita, apresentando-se em sua versão simples, quadrática e cúbica. Nesse modelo, os coeficientes não se apresentaram significativamente para a análise, assim, outro modelo (modelo 2) será apresentado, levando em conta apenas a forma simples do ln do PIB per capita e sua forma quadrática, ou seja, a segunda equação é uma forma quadrática do modelo apresentado. Os resultados de ambos os modelos podem ser vistos na Tabela 2.
Nos dois modelos estimados, o P-valor de F mostra que a probabilidade de aceitar a hipótese de que os coeficientes sejam iguais a zero é muito baixa (Prob > F = 0,0000). Ambos os modelos têm alto grau de confiabilidade. O modelo 1 tem uma explicação de 88,84% (R²=0,8884), enquanto o modelo 2, uma explicação de 88,83% (R²=0,8883). Assim, podemos afirmar que ambos os modelos têm um alto grau de explicação.
No modelo 1, os 𝛽𝑠equivalentes ao PIB per capita não são significativos a 10%, somente o PIB per capita do agronegócio tem significância de 10%, assim sendo, o modelo não teria explicação alguma da relação entre PIB per capita e desmatamento per capita. No modelo 2, a variável X3 (forma cúbica do ln do PIB per capita) foi desconsiderada, assim β1 foi significativo a 1%, com um impacto de -3,800629 no desmatamento, e β2 também significativo a 1%, com um impacto de 0,2608639 no desmatamento per capita. Sendo assim, não há evidências de que a CKA se apresentaria na forma de “U” invertido ao longo prazo, uma vez que β1 é negativo, β2 é positivo e β3 é insignificante.
Foram feitos os testes de Breusch-Pagan e White/Koenker para testar a hipótese de heterocedasticidade e o teste de White para autocorrelação, tendo sido verificado que ambos os modelos são homocedásticos e têm autocorrelação, assim, foi adotado o modelo GMM (Método Generalizado dos Momentos) (Tabela 3).
Como observado na regressão utilizando o Método dos Mínimos Quadrados Ordinários (MQO), o primeiro modelo é insignificante para determinar a relação entre PIB per capita e desmatamento per capita. Os coeficientes são não significativos a 10% de significância, e o desmatamento nesse modelo seria explicado apenas pelo PIB per capita do agronegócio, com um impacto de 3,89879 km² no desmatamento para cada unidade de PIB per capita do agronegócio.
Tabela 2 Modelos clássicos (MQO) estimados para CKA de Mato Grosso do Sul.
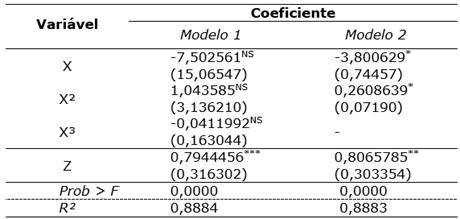
NS não significativo; * significativo a 1%; ** significativo a 5%; ** significativo a 10%;
X - PIB per capita Z - PIB do Agronegócio per capita.
Fonte: Resultados da pesquisa.
No segundo modelo, num primeiro momento, o PIB per capita tem relação negativa com o desmatamento em - 6,297587, com significância de 1%; em um segundo momento, apresenta uma relação positiva de 0,249791, sendo significativo a 5%. O PIB per capita do agronegócio continua, no segundo modelo, com uma relação positiva entre crescimento do PIB e desmatamento em 3,81306 km² para cada unidade.
Tabela 3 Modelo da Curva de Kuznets Ambiental para Mato Grosso do Sul (GMM).
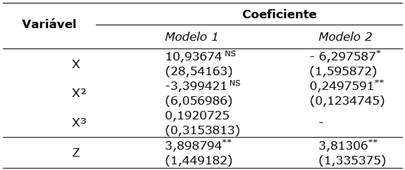
NS não significativo; * significativo a 1%; ** significativo a 5%; ** significativo a 10%; X - PIB per capita Z - PIB do Agronegócio per capita.
Fonte: Resultados da pesquisa.
O segundo modelo apresenta evidências de que a Curva de Kuznets ambiental não se apresenta em sua forma de “U” invertido para a relação entre desmatamento e crescimento econômico nas cidades do estado de Mato Grosso do Sul. Tendo âncoras este cenário e a política de proteção ao bioma, a tendência é que, com o passar dos anos, os dados do desmatamento sejam menores.
A existência de uma evidência de que a CKA não se apresenta em sua forma tradicional para o estado de Mato Grosso do Sul pode ser explicada pelo fato de a curva se apresentar em seu estágio inicial, uma vez que a economia do estado de MS ainda é extremamente dependente do setor agrícola, que impulsiona o setor industrial e o setor de serviços, onde explicam que a correlação entre crescimento econômico e pressão ambiental aumentaria quando o setor industrial passasse a exigir mais da agricultura, evidenciando que o estado tem características de uma economia ainda em desenvolvimento, ainda no estágio inicial da Curva de Kuznets Ambiental.
CONCLUSÕES
No presente estudo se observa que, predominantemente, as regiões Cone Sul e Sul-Fronteira, onde o bioma Mata Atlântica é predominante, não apresentaram um desmatamento muito elevado, ou seja, o desmatamento nessa região pode ser considerado consolidado, e não apresentará elevações consideráveis.
A significância do primeiro modelo adotando a forma cúbica do PIB per capita para explicar a relação do crescimento econômico e o desmatamento não foi suficiente para a análise, assim optou-se pelo segundo modelo, desconsiderando a forma cúbica da variável, e como β1 foi menor que o β2, podemos afirmar que, no estado de Mato Grosso do Sul, por ser um estado ainda dependente da agricultura, a Curva de Kuznets Ambiental se apresenta em seu estágio inicial, ou seja, não se apresenta na sua maneira tradicional, formato de “U”.
O fato de o PIB per capita do setor agrícola e o do setor de comércio e serviços serem mais significantes para a maioria das cidades do estado de Mato Grosso do Sul mostra que o estado ainda é dependente de uma economia agrícola, com características de uma economia ainda pouco desenvolvida, por esse motivo, o PIB per capita ao cubo foi insignificante, assim, podemos afirmar a hipótese da existência de uma Curva de Kuznets Ambiental com o formato de “U” invertido para o estado de Mato Grosso do Sul foi rejeitada.