Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Internacional de Investigación en Ciencias Sociales
versão On-line ISSN 2226-4000
Rev. Int. Investig. Cienc. Soc. v.9 n.2 Asunción dez. 2013
ANÁLISIS
Modelamiento basado en Agentes: un método de simulación computacional para la gestión de seguridad ciudadana
Agent-based Modeling: a computer simulation method for the management of public safety
Enrique Canessa1 y Ariel Quezada2
1. Facultad de Ingeniería y Ciencias, Universidad Adolfo Ibáñez, Chile.
2. Escuela de Psicología, Universidad Adolfo Ibáñez, Chile.
Correspondencia: Enrique Canessa. E-mail: ecanessa@uai.cl
Recibido: 17/01/2013; Aceptado: 26/07/2013.
Resumen: Este artículo presenta el Modelamiento basado en Agentes (MbA) como una herramienta útil para analizar sistemas sociales y el impacto de posibles intervenciones sobre estos. Para ilustrar la potencia del MbA se entrega un ejemplo didáctico de una posible dinámica de control de delincuencia y gestión de recursos para esto. Aplicando los resultados del MbA se ejemplifica el análisis de una posible gestión comunitaria de seguridad pública. Este modelo muestra cómo emergen cuatro dinámicas al manipular el monto de la recompensa entregada al contingente policial al capturar delincuentes. Al aumentar la recompensa, se encontraron umbrales abruptos que marcan la transición entre las siguientes dinámicas: a) extinción de policías; b) coexistencia de policías y ladrones; c) extinción de policías y ladrones; y d) extinción de ladrones. Se concluye que el MbA ayuda en la planificación de recursos para intervenciones comunitarias y/o en la investigación de las bases de dinámicas sociales no lineales.
Palabras clave: Modelamiento basado en Agentes, Dinámicas Sociales no lineales, Gestión Comunitaria, Seguridad Ciudadana.
Abstract: This paper presents Agent-based Modeling (ABM) as a useful tool for analyzing social systems and the impact of possible interventions on such systems. To illustrate the power of ABM, the paper uses a didactic example of resource management applied to delinquency control. Using the ABM’s results the paper shows the analysis of possible resource management for public security. This model shows how four types of dynamics appear as the value of the reward for catching thief increases, with abrupt thresholds between each of them: a) police extinction; b) co-existence of police and thief, c) police and thief extinction, and d) thief extinction. The paper concludes that ABM may help in the planning of resources in social interventions and/or research aimed at explaining the basis of non-linear social dynamics.
Key words: Agent-based Modelling, Non-linear Social Dynamics, community management, citizen security.
INTRODUCCIÓN
Desde la perspectiva de una agencia de seguridad ciudadana frente al incremento de los robos en su localidad, su principal tarea es la gestión de recursos para el control y prevención del delito. Por ejemplo, requerirá optimizar el uso de los recursos para invertir en personal de seguridad, y así disminuir los robos. De esta manera, debe tomar rápidamente decisiones que involucran, entre otras, la cantidad de policías, los incentivos que se le entregarán para capturar delincuentes, la cantidad de delincuentes, la posible tasa de incremento en la cantidad de policías y ladrones, y la cantidad de bienes materiales susceptibles de ser robados y el ritmo de crecimiento de dicha cantidad, entre otros factores.
La situación deseable sería contar con todos los datos reales para poder tomar decisiones, pero la obtención de los mismos es difícil y costosa. Probablemente, se conseguiría una pequeña cantidad de datos y aislados en el tiempo, lo que dificultaría analizar la dinámica del fenómeno. Además, la recolección longitudinal de datos con frecuencia se ve enfrentada a la denominada mortalidad experimental, lo que reduce los alcances y generalización de los resultados obtenidos (Waizmann & Roussos, 2005). Esto también se agrava al realizar estudios en la comunidad, ya que generalmente existen muchas variables difíciles de controlar, lo que limita aún más la validez de los resultados (Zwijze-Koning & De Jong, 2005). Finalmente, dada la cantidad de variables que el director de la agencia podría considerar en su gestión, resultaría difícil caracterizar el fenómeno delictual, ya que se necesitarían varios estudios que manipulen muchas variables. Esto puede ser engorroso, dado que es fácil intuir las dificultades para establecer, por ejemplo, una cierta proporción entre ladrones y policías en el área. Incluso algunas variables podrían no ser manipulables en la realidad, ya sea por imposibilidad material o ética, puesto que las intervenciones reales tendrían consecuencias sociales y políticas mayores. El establecer una gran cantidad de policías por cada delincuente ejemplificaría una imposibilidad material. Por otra parte, definir variables que permitan un gran aumento de la delincuencia para probar escenarios posibles, sería una restricción ética. Sin embargo, hacer lo anterior como “experimentos de pensamiento” (thought experiments) ayudaría a la agencia de seguridad a entender mejor el fenómeno y eventualmente tomar mejores decisiones, tal como indica Axelrod (1997). Así, estos experimentos pueden asistir la visualización preliminar de las consecuencias de intervenciones en la comunidad y dichos resultados servirían para comunicar mejor sus ideas a otros actores involucrados, permitiendo una mejor discusión de iniciativas, revelando aspectos inesperados del fenómeno. Incluso, desde una perspectiva de investigación social, la experimentación previa podría ayudar a focalizar estudios empíricos, permitiendo generar hipótesis tentativas y seleccionar posibles variables a manipular, develando sus posibles consecuencias (Canessa & Riolo, 2003; Canessa & Riolo, 2006).
Una herramienta y metodología que permite realizar adecuadamente lo anterior es el Modelamiento basado en Agentes (MbA). El MbA permite comprender la dinámica de un sistema para posteriormente diseñar e implementar las intervenciones necesarias y alcanzar así el estado deseado (Canessa & Riolo, 2006). Conocer las posibles trayectorias para llevar a un sistema desde un estado actual a uno futuro permitirá seleccionar aquella que sea más eficiente y eficaz para conseguir el estado deseado, evitando el tránsito por condiciones perjudiciales. Dadas las dificultades ya mencionadas en el análisis longitudinal de sistemas sociales, el MbA entrega la posibilidad de lidiar con varios de dichos problemas. El MbA consiste en desarrollar un programa computacional que permite crear pequeñas rutinas las cuales representan actores, o también llamados agentes. Estos agentes son capaces de tomar decisiones en forma autónoma, relacionarse entre ellos y guardar diferentes estados internos que se pueden alterar por la interacción con otros agentes, según reglas definidas por el programador (Berlekamp, Conway & Guy, 1982; Vallacher & Nowak, 1997). Los estados internos de los agentes pueden incluir preferencias, creencias, memoria de eventos recientes y conexiones sociales (Canessa & Riolo, 2006).
Desde las ciencias sociales ha habido acercamientos al MbA a partir de los modelos sociológicos de segregación social de Schelling (1978), los cuales han servido para comprender cómo dicho fenómeno se da en la realidad y a diseñar políticas tendientes a evitarlo. En psicología social Latané (1981) ha empleado el MbA para caracterizar dinámicas de influencia social, y Arrow, McGrath & Berhdal (2000) lo han utilizado en el estudio de la dinámica de grupos pequeños, lo que ha propiciado posteriores desarrollos en la gestión de equipos de trabajo y su influencia sobre el desempeño (Ilgen & Hulin, 2000; Ilgen, Hollenbeck, Johnson & Jundt, 2005). Una buena compilación de modelos aplicables a sistemas humanos y su gestión se encuentra en el trabajo de Phillip Ball (2003). Cabe señalar que el MbA ha sido poco explorado entre los investigadores sociales en Latinoamérica, aunque su uso en las ciencias administrativas en Europa y E.E.U.U. de N.A. comenzó con fuerza en las dos últimas décadas del siglo XX.
Al tener un MbA se pueden realizar extensas simulaciones que permiten obtener datos suficientes para caracterizar la dinámica comportamental del sistema. Ahora bien, esto no significa el abandono de los datos provenientes del sistema real o la pretensión de un pronóstico exacto de los valores puntuales del sistema. Si bien lo que permite un MbA está lejos de esto, lo que puede hacer es algo no menos importante: describir el patrón dinámico del comportamiento del sistema, es decir, el movimiento longitudinal que tendrán los datos, pero no exactamente el valor de ellos (Meyer, Gaba & Colwell, 2005).
Para lograr lo anterior, el modelo debe ser válido, es decir, se requiere que los resultados del MbA se acerquen suficientemente bien a los resultados que se podrían obtener en un sistema real (Bankes, 2002; Grimm et al., 2005; Grimm & Railsback, 2005). Como en el estudio de sistemas sociales pueden estar involucradas muchas variables, conocerlas e incluirlas a todas ellas complicaría al MbA a tal punto que sería difícil comprender los resultados de éste (Axelrod, 1997). Por esta razón, generalmente los MbA se usan para entender un sistema en vez de predecir valores exactos de este (Axelrod, 1997). En efecto, se puede alcanzar lo que se denomina equivalencia relacional o, en otras palabras, aquella que permite analizar si el comportamiento del modelo calza apropiadamente con el del sistema real (Grimm & Railsback, 2005). Por ejemplo, si el aumento de un parámetro del MbA causa un incremento en una variable de salida, el mismo cambio debería darse cualitativamente en el sistema real.
La elección de trabajar con MbA responde a la necesidad de utilizar una herramienta que permite describir el surgimiento de comportamientos del tipo Bottom Up, es decir, aquellos que emergen del funcionamiento y operación de unidades individuales. Esto desde las ciencias sociales significa que un comportamiento social se ve generado por el actuar de sujetos individuales en interacción y perturbación mutua. Es por esta razón que resulta tan natural y útil el uso de MbA en ciencias sociales y, en consecuencia, en las ciencias de la administración, dado que posibilita estudiar cómo se expresa el comportamiento agregado de los agentes del sistema, como asimismo, analizar el comportamiento individual de cada uno. Así, un MbA permite un fácil cambio en el nivel de análisis: se puede focalizar tanto en el nivel macro como en el micro. Esto es de gran utilidad cuando se quiere anticipar los resultados que una intervención tendrá en una comunidad o en una organización.
Descripción de un MbA que modela el control de delincuencia
El modelo da un ejemplo estilizado de la posible dinámica en la gestión de recursos para el control de la delincuencia, basándose en un modelo ecológico de presa-predador desarrollado por Wilensky & Reisman (1999). Comenzando con dicho modelo, se programó el presente MbA, tratando de usar la mayor abstracción posible, incluyendo el mínimo de variables y simplificando al máximo el modelo; aplicando el principio KISS, Keep It Simple, Stupid! (Axelrod, 1997), que insta a que los MbA sean lo más simples posible para que ayuden a entender el fenómeno que modelan. Además, un MbA sencillo facilita una introducción a esta técnica y ejemplifica mejor su uso, no pretendiendo el presente artículo ocupar el modelo para sacar conclusiones sustantivas.
En síntesis, este MbA representa a un área geográfica donde existen ladrones (delincuentes) y policías (personal de seguridad). A su vez, dicha área produce riqueza a una cierta tasa. Para sobrevivir, ladrones y policías deben mantener un nivel de energía sobre cero (de lo contrario se extinguen), para lo cual los ladrones necesitan robar dicha riqueza y los policías deben capturarlos. Ambos van consumiendo energía al moverse por el área. Tanto ladrones como policías aumentan según una cierta tasa. La Figura 1 muestra una pantalla del MbA implementado usando la plataforma de simulación Netlogo versión 4.0.2 (Wilensky, 2007), que es una plataforma de desarrollo de MbA de fuente abierta y totalmente gratuita.
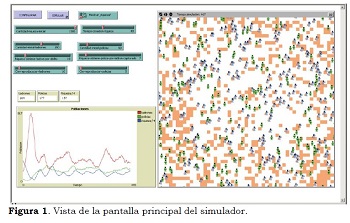
Para entender y analizar el MbA, se describirán el modelo y los agentes creados. Esto es parte del proceso de especificación de un MbA, donde debe estipularse las reglas de comportamiento e interacción entre agentes y las del espacio donde existirán estos.
- Ladrón: este agente representa a los delincuentes, caracterizado por una figura humana azul. Los ladrones se mueven dentro de la ventana derecha de la Figura 1. El número inicial de ladrones se establece usando el botón Cantidad-inicial-ladrones (botones en la parte izquierda de la Figura 1). Cada ladrón tiene asignado un nivel de energía inicial, muestreado de una distribución uniforme entre cero y el doble de la riqueza que obtendrá al cometer un robo. El ladrón se mueve aleatoriamente por el área, reduciendo en una unidad su energía cada vez que lo hace y, al encontrar riqueza (cuadrado anaranjado) la roba, aumentando su energía según lo establecido por el botón Riqueza-obtiene-ladron-por-delito. En todo ciclo de simulación, los ladrones aumentan según un porcentaje establecido por el botón Cte-reproduccion-ladrones. El ladrón es eliminado si su energía llega a cero o si es capturado por un policía.
- Policía: este agente representa a los encargados de controlar la delincuencia, caracterizado por una figura humana verde. Los policías se mueven en la misma área que los ladrones. El número inicial de policías se administra usando el botón Cantidad-inicial-policias. A cada policía se le asigna un nivel de energía inicial, muestreándolo de una distribución uniforme entre cero y el doble de la energía que obtendrá al capturar un ladrón. El policía se mueve aleatoriamente por el área, reduciendo en una unidad su energía al desplazarse y, al coincidir con un ladrón lo captura, aumentando su energía según lo establecido por el botón Riqueza-obtiene-policia-por-ladron-capturado. En todo ciclo, la dotación de policías aumenta según un porcentaje dado por el botón Cte-reproduccion-policias. Si la energía del policía disminuye a cero, éste es borrado del área.
- Riqueza: la riqueza se representa por cuadrados anaranjados que se ubican aleatoriamente sobre el área en la cantidad dada por el botón Cantidad-riqueza-inicial. A su vez los cuadrados blancos, reciben un número muestreado de una distribución uniforme entre cero y una constante definida por el botón Tiempo-creacion-riqueza. En cada ciclo de simulación, estos números se disminuyen en uno y al llegar a cero, los cuadrados blancos se colorean de anaranjado, representando la generación de riqueza cada cierto tiempo. Cuando un ladrón se sitúa sobre un cuadrado anaranjado, sustrae dicha riqueza y el cuadrado se colorea de blanco, y luego se sigue el mismo procedimiento que simula la creación de riqueza. Por su parte, la máxima cantidad de riqueza que puede existir en el área equivale a la cantidad total de celdas de ésta.
- Área geográfica: es un toroide de 51 por 51 cuadrados (total de 51 x 51 = 2601 celdas), representado por la ventana derecha de la Figura 1, por lo que su borde izquierdo y derecho, así como el superior e inferior son adyacentes. Por ejemplo, un agente que se mueva hacia la derecha del toroide puede pasar del borde derecho al izquierdo y lo circunnavegará. Lo mismo sucede con los bordes superior e inferior. Cada cuadrado puede contener a varios policías y/o ladrones, los que se desplazan sobre el área moviéndose de cuadrado en cuadrado.
Los tres botones superiores mostrados en la parte izquierda de la Figura 1 realizan lo siguiente: el botón Configurar establece las condiciones iniciales de una corrida de simulación; el botón Simular inicia, pausa y detiene una corrida; el botón Mostrar_Riqueza señala al programa si debe o no mostrar el valor de la riqueza (energía) que cada ladrón y policía tiene durante una simulación. El gráfico ubicado en la parte izquierda inferior de la Figura 1 muestra las series de tiempo correspondientes a la cantidad de ladrones (línea roja), cantidad de policías (línea verde) y cantidad de riqueza dividida por cuatro (línea azul). El eje de tiempo del gráfico corresponde a los pasos (ciclos) de simulación desde el comienzo de una corrida. Las ventanas pequeñas ubicadas sobre dicho gráfico muestran los valores instantáneos correspondientes a esas mismas cantidades.
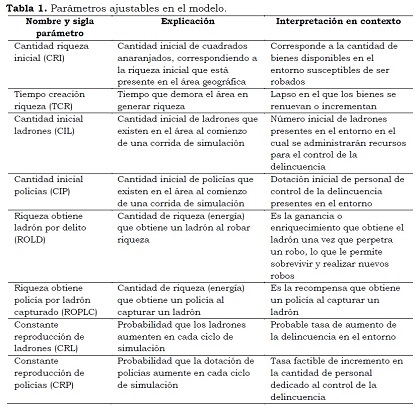
La Tabla 1 resume los parámetros del MbA y entrega una explicación de los mismos, junto con la correspondiente interpretación sustantiva en el contexto de la situación planteada de la gestión de control de la delincuencia.
Experimentos con el MbA y resultados
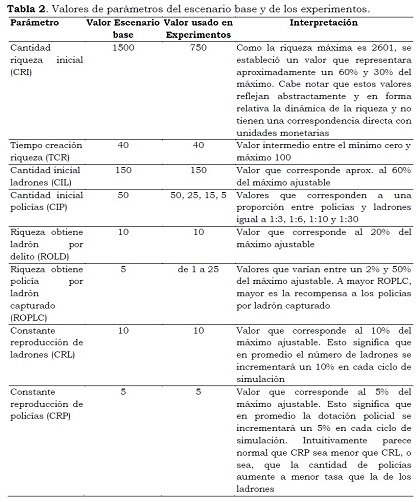
Una vez que los autores programaron y verificaron el MbA, realizaron corridas preliminares para vislumbrar la dinámica del modelo, variando los valores de los diferentes parámetros. Basados en esas corridas de simulación, se seleccionó un escenario base que reflejara intuitivamente un contexto real. Este es un paso inicial en la validación del MbA, lo que comúnmente se denomina validez de faz, o sea, que expertos en el tema concuerden con los supuestos del modelo. Esto facilita alcanzar equivalencia relacional entre el modelo y el sistema real. La Tabla 2 muestra los valores de parámetros establecidos para obtener dicho escenario.
La dinámica del escenario base se puede observar en la Figura 2. En general, la cantidad de policías es menor que la de ladrones y coexisten, no extinguiéndose ninguno de ellos. La cantidad de ladrones aumenta en un comienzo y luego oscila alrededor de un número mayor de ladrones que la inicial. A su vez, la cantidad de policías también oscila alrededor del número inicial establecido. En cuanto a la cantidad de bienes disponibles (riqueza), esta oscila en desfase con la cantidad de ladrones (los máximos de riqueza se producen al mismo tiempo que los mínimos de ladrones y viceversa). La riqueza fluctúa en un rango menor que la riqueza inicial.
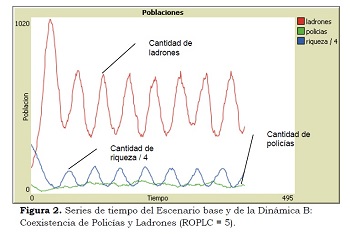
A este escenario se le ha llamado base, pues intuitivamente reproduce el contexto que es más probable de encontrar en cualquier ciudad: una cantidad de personal de control de la delincuencia menor que la cantidad de ladrones y una cantidad de bienes disponibles que es sensible a la cantidad de robos, pues disminuye cuando se realizan más delitos y aumenta su disponibilidad cuando hay menos. Esta situación seduce a los ladrones a realizar nuevos delitos, pues perciben más riqueza circulando. Como se ha mencionado, el foco del presente trabajo es mostrar el uso del MbA, y por ello no se pueden sacar conclusiones válidas del modelo aplicables directamente a una situación real. Sin embargo, el modelo permite realizar “experimentos de pensamiento” que ayudarán a tener una mejor noción de las posibles dinámicas del sistema.
Luego de haber establecido este escenario base, se manipuló el valor de tres variables, según muestra la Tabla 2. El uso de estas tres variables constituye solo un análisis inicial, por lo que un estudio acabado requeriría una exploración más amplia del espacio de parámetros. Los resultados se analizarán cualitativamente, evitando un análisis numérico y privilegiando resaltar la diferencia en la dinámica del sistema que produce la variación de parámetros, en vez de centrarse en valores puntuales. Por ejemplo, si el MbA muestra que la dinámica del sistema es oscilatoria, este comportamiento sería interesante de analizar; contrariamente a lo irrelevante que sería saber el valor final exacto de una variable. Esto ya que el MbA permite la descripción de la dinámica de un sistema, pero no predecir valores puntuales de variables.
En la manipulación de los parámetros según lo establecido en la Tabla 2, se notó que al ir variando ROPLC entre 1 y 25, emergieron umbrales bastante marcados, que configuraron cuatro dinámicas diferentes para el sistema.
Dinámica A: Extinción de Policías
A nivel macro, se observa que cuando ROPLC varía entre 1 y 4, los policías se extinguen, quedando en el largo plazo sólo ladrones, cuya cantidad oscila en desfase con la riqueza. Esto se puede apreciar en la Figura 3.
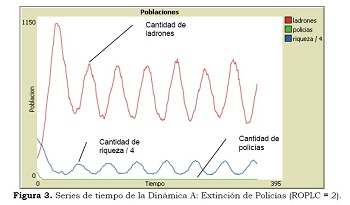
A continuación, para entender lo observado a nivel macro, se cambiará a un nivel de análisis micro, lo que pondrá de manifiesto la utilidad y facilidad del cambio en MbA. A nivel micro, se puede establecer que el MbA exhibe esta dinámica ya que los policías obtienen muy poca recompensa cada vez que capturan un ladrón. Por ello, su energía se agota muy rápido y no alcanzan a aumentar lo suficiente para reemplazar a los que desaparecen, con lo cual terminan extinguiéndose. Ahora bien, los ladrones persisten ya que no tienen policías que los capturen. Como los ladrones obtienen su energía de la riqueza existente, está disminuye y por ello, los ladrones también, sin llegar a extinguirse. Luego, al disminuir los ladrones y crearse nueva riqueza, esta aumenta. Con ello, hay más riqueza disponible para que los ladrones la roben, con lo que estos también aumentan, causando la oscilación de ladrones y riqueza con desfase entre los máximos de esas cantidades.
Esto se representaría en un barrio en el cual se invierte “simbólicamente” en personal de seguridad, con baja recompensa por capturar ladrones. De esta forma, dicho personal se desincentiva y renuncia y/o es cesado de sus funciones dado que disminuye su efectividad al estar desmotivado. Como consecuencia, los ladrones se ven afectados tan sólo por la cantidad de bienes disponibles, es decir, cuando hay muchos bienes puede haber más ladrones para sustraerlos hasta que, al disminuir la riqueza, hay poco que robar y, por ende, los delincuentes se reducen. Así, este ciclo se repite en el tiempo.
Dinámica B: Coexistencia de Policías y Ladrones
Cuando ROPLC varía entre 5 y 11, los policías y ladrones coexisten. Las cantidades de policías, ladrones y riqueza oscilan. Al igual que en la dinámica A, la cantidad de ladrones oscila en desfase con la riqueza. A su vez, los máximos de las series de tiempo de cantidad de ladrones y policías también están desfasadas. Los máximos de policías se producen un tiempo después que los máximos de ladrones. Esto se puede apreciar en la Figura 2. Además, comparando la Figura 2 (ROPLC = 5) con la Figura 4 (ROPLC = 11), se puede ver que a medida que ROPLC aumenta, la cantidad promedio de ladrones tiende a disminuir y la de policías y riqueza a aumentar. Por otra parte, nótese que la variabilidad temporal de las series parece aumentar: los máximos y mínimos de las series tienden a ser más extremos. En este caso, los policías obtienen suficientes recompensas para sobrevivir por un tiempo adecuadamente largo que les permita incrementarse en una cantidad que se balancee aproximadamente con la de los policías que van desapareciendo. Esto hace que los ladrones vayan siendo capturados, pero son repuestos por los nuevos ladrones generados, balanceando la cantidad de policías y ladrones: los policías no son tan numerosos para extinguir a los ladrones y éstos no son tan escasos para que los policías no tengan suficientes ladrones para capturar.
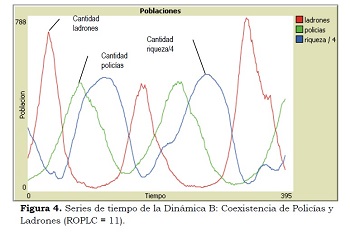
La dinámica oscilatoria de las series de tiempo se explica como en la dinámica A: los ladrones roban, disminuyendo la riqueza disponible, lo que reduce la cantidad de ladrones, ya que no tienen qué robar y cómo subsistir. Simultáneamente, la cantidad de policías aumenta y se capturan más ladrones, reforzando la disminución de estos. Al disminuir los ladrones, la riqueza aumenta y los policías se quedan sin muchos ladrones que capturar, con lo cual decrece su nivel de energía y comienzan a desaparecer. Esto hace que la cantidad de ladrones crezca y la riqueza disminuya, repitiéndose así el ciclo.
El incremento de ROPLC causa una disminución del promedio de ladrones y un aumento del promedio de policías y riqueza, pues los policías obtienen más recompensa por ladrón capturado, viviendo más tiempo e incrementándose más. Esto causa la disminución de ladrones, al existir más policías que los capturen y, al haber menos ladrones, la riqueza se incrementa.
Adicionalmente se observó que al incrementar ROPLC el rango (diferencia entre máximo y mínimo) de cada serie de tiempo crece, puesto que esta condición permite que los policías aumenten más, incrementando sus valores máximos. Esto influye también -como ya se explicó- en las cantidades máximas y mínimas de ladrones y riqueza. Es decir, la amplificación de los valores máximos y mínimos de policías, también se refleja en las series de tiempo de ladrones y riqueza.
Esto se vería reflejado en un vecindario en el cual hay una cantidad de bienes disponibles en el entorno que incita a los ladrones a robar. Simultáneamente se genera una estrategia de seguridad en la cual se contrata a un personal proporcionándoles mayores incentivos para capturar ladrones, lo que conlleva a que tengan más recursos para realizar su trabajo e incrementar su contingente. Una vez que los robos disminuyen los bienes disponibles, la cantidad de ladrones comienza a decrecer, lo que se acentúa por el incremento en la cantidad de policías. No obstante, el ciclo se renueva cuando la cantidad de ladrones disminuye de manera tal que la cantidad de bienes disponibles aumenta y vuelve a ser un incentivo suficiente para que surjan más ladrones. Los policías en ese momento ya han disminuido debido a que la baja en ladrones ha hecho innecesaria la presencia de contingente de seguridad sugiriendo a la agencia encargada de seguridad reducir el personal. Pero al aumentar los robos, la dotación policial es incrementada, repitiéndose el ciclo.
Dinámica C: Extinción de Policías y Ladrones
Cuando ROPLC varía entre 12 y 19, los policías y ladrones se extinguen. La dinámica de las series de tiempo muestra una oscilación similar a la descrita para la dinámica B, lo que se aprecia en la Figura 5. Además, se notó que a medida que ROPLC aumenta, en general, el tiempo de simulación para alcanzar la extinción disminuye. Como los ladrones se extinguen, la riqueza alcanza su máximo valor posible (2601).
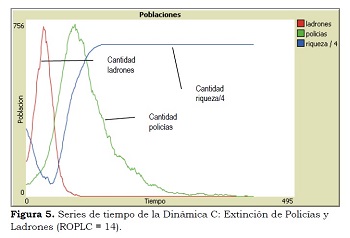
Esta dinámica emerge ya que la recompensa que obtienen los policías por ladrón capturado es tal que logran vivir y reproducirse por mucho tiempo, aumentando enormemente su cantidad. A su vez, este gran aumento de policías permite la captura de todos los ladrones antes que éstos se incrementen en cantidad suficiente para reponer a los capturados, con lo cual se extinguen. Por ello, al no haber más ladrones, los policías no obtienen más recompensas y desaparecen, mientras que la riqueza crece hasta su máximo posible.La dinámica anterior se vería ejemplificada en un barrio en el cual la existencia de ladrones se ve contenida por la presencia de un contingente de seguridad altamente incentivado y que captura a la totalidad de los ladrones. Sin embargo, este éxito haría innecesario dilapidar recursos para proteger a ciudadanos que ya no requerirían protección, lo que en definitiva terminaría por eliminar el servicio. En este escenario, al no haber ladrones que reduzcan la riqueza, ésta llega a su punto máximo.
Evidentemente esta es la situación ideal, pero altamente utópica pues debería suponer dos cosas: a) si se lograra la extinción de los ladrones, no habría incentivos para que surgieran otros, y b) por razones de Estado o políticas de un vecindario, no habría necesidad de tener un contingente de seguridad mínimo con el fin de b1) disuadir el surgimiento de ladrones y b2) generar una fuente adicional de trabajo.
Dinámica D: Extinción de Ladrones
Cuando ROPLC es mayor o igual a 20, los ladrones se extinguen, pero los policías crecen sin límite. Evidentemente que al extinguirse los ladrones la riqueza alcanza su nivel máximo, lo que se aprecia en la Figura 6.
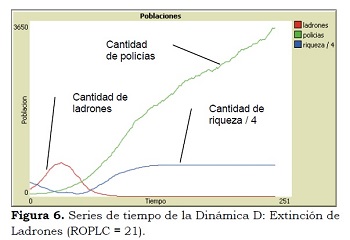
Al igual que en la dinámica C, los policías aumentan tanto que capturan a todos los ladrones antes que estos logren incrementarse en cantidad suficiente para reponer a los capturados. Sin embargo, a diferencia de la dinámica C, la cantidad de policías crece tanto en un comienzo, dado el alto valor de ROPLC, que alcanza un “número crítico”, tal que surgen más policías que los que van desapareciendo, con lo cual el número de policías crece sin límite. Este crecimiento ilimitado de policías se da incluso con la extinción de los ladrones. Aunque los policías no puedan obtener recompensa y vayan desapareciendo, se incorporan más que los que desaparecen, autoperpetuándose. Además, esta dinámica se genera ya que al establecer un valor alto de ROPLC, los policías creados inicialmente y los que van incorporándose tienen un alto nivel de energía, lo que les permite trabajar por mucho tiempo y mantenerse, alcanzando el número crítico necesario para autosostenerse.
Esta condición, tan utópica como la anterior, se daría si una comunidad da grandes incentivos para ser personal de seguridad. Así, la captura de un ladrón generaría un gran beneficio para el policía, obteniendo más recursos para tener una buena subsistencia. Esto tendría un efecto de “llamada” (appeal) para otros nuevos policías. Lo anterior aumentaría la cantidad de policías, permitiendo que la riqueza del vecindario aumente al máximo, ya que no habría nuevos robos. Esta generación de policías podría llegar a ser autosustentada pues, habiendo un gran número de ellos: a) tendrían una gran influencia para que no haya política de reducción de contingente, pues dejarían sin trabajo a mucha gente; y b) podría pensarse que una gran presencia policial disuade la llegada de nuevos ladrones, por lo cual, nunca debería disminuirse.
Además de las cuatro dinámicas descritas, la experimentación usando los valores establecidos en la Tabla 2, permitió analizar la influencia general de dichos parámetros sobre los resultados. En resumen, se pudo establecer lo siguiente:
- Las dinámicas A, B, C y D se dan tanto con una Cantidad de Riqueza Inicial (CRI) igual a 1500 y 750. Para esta parte del espacio de parámetros y en el rango analizado, CRI parece no tener mayor influencia en las dinámicas.
- En general, en todos los escenarios, la dinámica comportamental se ve autoorganizada por el propio sistema. Es decir, manipulando la variable ROPLC se logra llegar a determinadas dinámicas comportamentales que se pueden predecir, pero no pudiendo determinar exactamente la cantidad de policías, ladrones y riqueza que se obtendrán en un determinado momento.
- Al disminuir CIP, los umbrales que fijan el paso de una dinámica a otra se vuelven menos precisos. Esto significa que en los umbrales de cambio de dinámica (ROPLC = 4, 5; 11, 12; 19 y 20), la probabilidad que una corrida de simulación genere una dinámica distinta, tiende a disminuir. Por ejemplo, si se fija ROPLC = 4 y CIP = 50, si se hacen 10 corridas, todas exhibirán la dinámica A. Si ahora CIP = 5, alrededor de 7 corridas exhibirán la dinámica A y 3 la dinámica B. Nótese que los saltos son siempre entre dinámicas adyacentes, es decir, A a B, B a C, y C a D, pero nunca, por ejemplo, de A a C o de C a D. Cabe agregar que se experimentó con menores valores de CIP, ya que se quiso usar escenarios cada vez más cercanos a un contexto comunitario real, al tener proporciones de policías a ladrones iguales a 1:3, 1:6, 1:10 y 1:30.
CONCLUSIONES
Volviendo al ejemplo inicial de la agencia de seguridad ciudadana, los resultados de este MbA le ayudarán a comprender mejor las dinámicas de control de delincuencia y atisbar posibles intervenciones. Entonces, basándose en dichos resultados preliminares, la agencia podrá diseñar más certeramente estudios empíricos para analizar y gestionar la situación que enfrenta. Las conclusiones preliminares más importantes que tendrá dicha agencia son las siguientes:
a) La presencia de delincuentes y el nivel máximo de riqueza disponible en el entorno depende del monto de la recompensa que recibe el personal de seguridad por atrapar a los delincuentes, lo que se podría interpretar como un personal incentivado o no en su trabajo y, por ende, más o menos eficaz. Esto se da en distintos escenarios base y en distintas condiciones iniciales, con lo que se recomienda un personal bien recompensado e incentivado a ser eficaz, por sobre un gran contingente con pocos incentivos y con un pobre rendimiento. Cabe destacar que un revisor planteó que tal vez al haber una gran recompensa por capturar delincuentes, el personal de seguridad podría tratar de aumentar la delincuencia para obtener más recompensas. Aunque esa situación es posible, estimamos que es menos factible que el escenario base indicado. De todas formas, justamente una ventaja del MbA es que se puede modificar fácilmente el modelo para incorporar dicha situación y ver el efecto que tendría sobre los resultados.
b) En base a la cantidad inicial de bienes disponibles que se ha manipulado (30 y 60% del máximo), se puede postular que ésta no influye mucho en su valor a largo plazo y en la dinámica del sistema. Es decir, a largo plazo, la cantidad de bienes disponibles llega a un determinado nivel según la dinámica que emerja, con independencia de su cantidad inicial. Esto significaría que para ciudades y barrios que mantengan esta “distancia” en cuanto a riqueza, igualmente se observarán dinámicas homologables. Por ello, la agencia de seguridad ciudadana no encontraría diferencias significativas si trabaja en una ciudad, comuna o barrio de una riqueza disponible catalogable como media alta y media baja.
c) Existen no linealidades en la dinámica del control de la delincuencia. Esto es, una modificación en los incentivos para atrapar ladrones genera cambios dramáticos en la dinámica delincuencial, lo que no es gradual, sino que se da en umbrales o límites. En otras palabras, y sólo a modo de ejemplo, los resultados que pueden obtenerse al implementar un contingente con policías medianamente motivados sería totalmente distintos que tener la misma cantidad de policías algo más incentivados.
Complementando lo discutido sobre la validez de un MbA, nótese que para poder aplicar los resultados anteriores a un contexto real, se requiere establecer equivalencia relacional con el sistema. Esto sólo se hizo preliminarmente al establecer el escenario base intuitivo. Por lo tanto, a nivel macro, se debería recolectar cierta cantidad de datos para compararlos con las series temporales que generó el MbA. Asimismo, a nivel micro, habría que sustentar teóricamente el comportamiento asignado a cada agente (Canessa & Riolo, 2006), en este caso, policías, ladrones y riqueza. Dado lo anterior, de observar algún resultado no intuitivo, se debería evaluar si la inferencia inicial es la incorrecta, o bien, si dicha inferencia fuera la apropiada. En este último caso, se debería ajustar el modelo para que los resultados concuerden con la inferencia.
En relación a la herramienta para efectuar MbA, se recomienda fuertemente Netlogo, la cual permite hacer Thought Experiments de manera simple. Esto queda de manifiesto al considerar que el presente modelo requirió de aproximadamente 40 horas de trabajo para ser implementado, incluyendo el aprendizaje de Netlogo. Es más, esta simpleza permitiría que con facilidad se le agregaran a este MbA varios aspectos adicionales si se estimase necesario para un mejor calce con la realidad. Por ejemplo, se podría modelar el encarcelamiento de los ladrones, haciendo que desaparezcan del área por un tiempo y luego sean reinsertados. Sumado a lo anterior, se agrega que esta herramienta es completamente gratuita, es de fuente abierta y se encuentra disponible para plataformas PC, Macintosh y sistemas operativos de uso común. Además, posee una excelente documentación y soporte a través de la web. Al respecto, los autores han empleado otras plataformas para MbA tales como Swarm y Repast, y coincidiendo con otros investigadores de ciencias sociales, Netlogo parece ser una excelente alternativa por su sencillez de uso, permitiendo que los investigadores se concentren en estudiar un sistema, en vez de distraerlos demasiado en programar el modelo (Robertson, 2006; Railsback, Lytinen & Jackson, 2007).
A la luz de las conclusiones obtenidas, queda claro que una dinámica que inicialmente puede parecer simple podría evidenciar un comportamiento de mayor complejidad, para lo cual el MbA puede facilitar su comprensión preliminar (Meyer, Gaba & Colwell, 2005). Precisamente este trabajo muestra la aplicación de MbA a la comprensión y posterior intervención en sistemas sociales, especialmente cuando se sospecha que exhiben no linealidades. En particular, para las ciencias sociales y la práctica administrativa esto es muy relevante dado que frecuentemente se enfrentan con dinámicas no lineales y, además, con una gran dificultad para llevar a cabo análisis y acciones en el sistema real (Meyer, Gaba & Colwell, 2005). Esta particularidad hace difícil la comprensión de dinámicas sociales que operan en comunidades y organizaciones, requiriéndose un análisis más profundo para lograr una apropiada gestión de estas.
Ante esta situación, el MbA y Netlogo, como una herramienta de fácil acceso y uso, ayudan a visualizar posibles dinámicas que emergen en una relación micro-macro (bottom-up) por la acción y perturbación mutua entre los agentes constitutivos de un sistema social, ya sea comunidad u organización. Sin que el MbA se erija como un instrumento que reemplace al análisis con datos reales o que permita pronósticos acabados y exactos de comportamientos sociales, la propuesta de este artículo es precisamente presentar una herramienta que favorezca el análisis preliminar de fenómenos que ocurren en grupos, comunidades y organizaciones, ayudando a su posterior gestión.
REFERENCIAS
Arrow, H., McGrath, J.E. & Berdahl, J.L. (2000). Small Groups as Complex Systems: formation, Coordination, Development and Adaptation. London: SAGE. [ Links ]
Axelrod, R. (1997). Advancing the Art of Simulation in the Social Sciences (21-40). En Conte, R., Hegselmann, R & Terna, P. Simulating Social Phenomena. Berlin: Springer-Verlag. [ Links ]
Ball, P. (2003). The Physical Modelling of Human Social Systems. Complexus, 1,190-206. [ Links ]
Bankes, S.C. (2002). Agent-Based Modeling: a revolution?. PNAS, 99, 3, 7199-7200. [ Links ]
Berlekamp, E., Conway, J. & Guy, R. (1982). Winning ways for your mathematical plays, Games in Particular 2. London: Academic Press. [ Links ]
Canessa, E. & Riolo, R. (2003). The effect of Organizational Communication Media on Organizational Culture and Performance: An agent-based simulation model. Computational and Mathematical Organization Theory, 9, 147-76. [ Links ]
Canessa, E. & Riolo, R. (2006). An agent-based model of the impact of computer-mediated communication on organizational culture and performance: an example of the application of complex systems analysis tools to the study of CIS. Journal of Information Technology, 21, 272-83. [ Links ]
Grimm, V. & Railsback, S.F. (2005). Individual-Based Modeling and Ecology. Princeton, NJ: Princeton University Press. [ Links ]
Grimm, V., Revilla, E., Berger, U., Jeltsch, F., Mooij, W.M., Railsback, S.F., Thulke, H.H., Weiner, J., Wiegand, T. & Deangelis, D.L. (2005). Pattern-Oriented Modeling of Agent-Based Complex Systems: Lessons from ecology. Science, 310, 987-991. [ Links ]
Ilgen, D.R. & Hulin, C. (2000). Computational modeling of behavior in organizations, Washington D.C.: American Psychological Association. [ Links ]
Ilgen, D. R., Hollenbeck, J. R., Johnson, M. & Jundt, D. (2005). Teams in Organizations: From Input-Process-Output Models to IMOI Models. Annual Review of Psychology, 56, 517-43. [ Links ]
Latané, B. (1981). The psychology of social impact. American Psychologist, 36, 343-65. [ Links ]
Meyer, A.D., Gaba, V. & Colwell, K.A. (2005). Organizing Far from Equilibrium: Nonlinear change in organizational frontiers. Organization Science, 16, 456-75. [ Links ]
Railsback, S., Lytinen, S. & Jackson, S. (2007). Agent-based Simulation Platforms: review and Development Recommendations. Disponible en la red: www.humboldt.edu/~ecomodel/documents/ABMPlatformReview.pdf [ Links ]
Robertson, D. (2006). Agent-Based Modeling Toolkits NetLogo, RePast, and Swarm. Academy of Management Learning & Education, 4, 525-27. [ Links ]
Schelling, T.C. (1989). Micromotivos y macroconducta. México, D.F.: Fondo de Cultura Económica, S. A. de C. V. (Orig. 1978). [ Links ]
Vallacher, R.R. & Nowak, A. (1997). The Emergence of Dynamical Social Psychology. Psychological Inquiry, 8, 73-99. [ Links ]
Waizmann, V. & Roussos, A.J. (2005). Preparación de artículos científicos en Psicología clínica, Documento de Trabajo N° 135, Universidad de Belgrano, Disponible en la red: http://www.ub.edu.ar/investigaciones/dt_nuevos/135_waizmann.pdf [ Links ]
Wilensky, U. (2007). Netlogo, http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL. [ Links ]
Wilensky, U. & Reisman, K. (1999). Connected Science: Learning Biology through Constructing and Testing Computational Theories - an Embodied Modeling Approach. International Journal of Complex Systems, M. 234, 1-12. [ Links ]
Zwijze-Koning, K.H. & De-Jong, M.D.T. (2005). Auditing Information Structures in Organizations: a review of data collection techniques for network analysis. Organizational Research Methods, 8, 429-53. [ Links ]