Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista Internacional de Investigación en Ciencias Sociales
On-line version ISSN 2226-4000
Rev. Int. Investig. Cienc. Soc. vol.8 no.1 Asunción July 2012
ARTÍCULO ORIGINAL
Tendencias actuales de la enseñanza-aprendizaje de la geometría en educación secundaria
Current trends in the teaching and learning of Geometry at Secondary School level
Manuel Barrantes-López(1)
Idalgo Balletbo-Fernández(2)
1. Doctor en Matemáticas. Facultad de Educación. Universidad de Extremadura. Badajoz. España. E-mail: barrante@unex.es.
2. Máster Univ. en Investigación para la Enseñanza y Aprendizaje de las Ciencias Experimentales, Sociales y Matemáticas por la Universidad de Extremadura. Máster en Educación Superior por la Universidad Autónoma de Asunción. Docente de la Fac. de Ciencias Aplicadas y de la Fac. de Ciencias Contables, Admistrativas y Económicas. Universidad Nacional de Pilar. Ñeembucú-Paraguay. E-mail: ipsjb@yahoo.es
Correspondencia: Idalgo Balletbo Fernández. Dirección: Dr. Victor Z. Romero e/ Avda. Mons. Rojas Nro. 402. San Juan Bautista. Misiones - Paraguay
Recibido: 20/03/2012. Aceptado: 04/05/2012.
Resumen: Realizamos una revisión bibliográfica y una reflexión de los últimos trabajos sobre la enseñanza y el aprendizaje de la geometría en la Enseñanza Secundaria que pudiera servir como referencia de base teórica para tesis, proyectos y otros trabajos académicos, en la que se brinda al investigador datos actualizados sobre temas relacionados con el área de didáctica de la geometría según: diferentes materiales y medios como facilitadores de las actividades de aprendizajes. También, el profesor de Secundaria, tiene un material a su alcance que presenta propuestas nuevas y adecuadas, que le garantizan mejores resultados en su actividad docente y de desempeño en el aula.
Palabras clave: Educación matemática, enseñanza, aprendizaje, geometría.
Abstract: We conducted a literature review of recent work on teaching an learning of geometry in secondary schools that could serve as reference for theoretical theses, projects and other academic work, in which the researcher provides an update on issues related to the area of teaching of geometry according to: type of materials and media as facilitators of learning activities. Also, the secondary teacher has a material at its disposal that presents new and appropriate proposals will ensure better results in their teaching and classroom performance.
Keywords: Mathematics education, teaching, learning, geometry.
INTRODUCCIÓN
La educación matemática en la última década ha sido objeto de varias investigaciones en el ámbito de la caracterización y clasificación de contenidos específicos relacionados a potencializar la enseñanza–aprendizaje, en especial en el área de la Geometría, la cual es parte integrante de la cultura de la humanidad, no sólo por su función instrumental sino también porque incentiva el desarrollo del pensamiento crítico y creativo, a fin de comprender y modificar el entorno.
La principal finalidad de la enseñanza-aprendizaje de la geometría es conectar a los alumnos con el mundo en el que se mueven pues el conocimiento, la intuición y las relaciones geométricas resultan muy útiles en el desarrollo de la vida cotidiana (Barrantes, 2003).
Consideramos que la geometría, además de estar presente en múltiples facetas de la vida actual, tiene una gran influencia en el desarrollo del educando, sobre todo en las capacidades relacionadas con la comunicación y la relación con el entorno. La geometría favorece y desarrolla en los alumnos una serie de capacidades como la percepción visual, la expresión verbal, el razonamiento lógico y la aplicación a problemas concretos de otras áreas de Matemáticas o de otras materias.
Por ello, se ha considerado de interés realizar un análisis bibliográfico de los últimos trabajos sobre la enseñanza y el aprendizaje de la geometría que pudiera servir como referencia de base teórica para tesis, proyectos y otros trabajos académicos, mediante la que se brinda al investigador y docente, datos actualizados con informaciones en base a una clasificación bibliográfica sobre temas relacionados al área de Geometría, según los diferentes materiales y medios como facilitadores y actividades de los aprendizajes y según los niveles y contenidos específicos establecidos en el currículo de la Comunidad Autónoma Extremeña (España).
En los contenidos de la enseñanza–aprendizaje de la geometría se pretende establecer una serie de destrezas cognitivas de carácter general que puedan ser utilizadas en muchos casos particulares y que contribuyan por sí mismas a desarrollar las capacidades. La línea general de trabajar la geometría es desde una metodología de resolución de problemas, mediante la que el alumno, además de estar motivado, aprende.
Actualmente y en congruencia con una metodología activa de enseñanza se tiende a trabajar con materiales que desarrollen una geometría dinámica (Damiani et-al., 2000). Diversos programas de ordenador como Cabri o GeoGebra contribuyen a desarrollar esta metodología activa mediante el dinamismo que dan a las actividades geométricas que se pueden desarrollar con dichos programas. Así el Instituto de Tecnología Educativa (ITE) español, ha desarrollado el Proyecto Gauss (http://recursostic.educacion.es/gauss/web/) que brinda al profesorado muchas actividades de interés didáctico, realizadas con GeoGebra para Primaria y Secundaria, que cubren todos los contenidos de Matemáticas de esos niveles educativos y están diseñadas para ser utilizadas tanto en la pizarra digital como en los ordenadores de los alumnos.
Por otra parte y en esta misma línea, Fortuny (1998) nos presenta y analiza una selección de recursos y materiales orientados a la facilitación, activación y desarrollo de procesos clave de la educación de las competencias geométricas, como son las de visualizar, explorar y modelizar. Diversas investigaciones (Alsina et-al., 1988; Fernández et-al., 1991; Calvo, 1996) coinciden en que la geometría sirve para interpretar y actuar sobre el espacio, y que la utilización de materiales favorece la interacción del medio con el alumno y dan lugar a un aprendizaje más significativo.
El objetivo principal de este trabajo es la clasificación y análisis de los artículos españoles de contenidos relacionados con la enseñanza-aprendizaje de la geometría establecidos en revistas científicas de mayor impacto de la última década.
METODOLOGÍA
Esta investigación se realizó en base a las revistas de mayor impacto indicadas en la página web de In-Recs, independientemente de otras fuentes. In-Recs permite saber cuál es el impacto científico de una revista, su evolución y su posición respecto al resto de las revistas de la especialidad a través de distintos indicadores bibliométricos. La idea de seleccionar así las revistas no es tanto, considerar el impacto de la revista, sino garantizar que las revistas importantes (las de mayor impacto) estuvieran dentro de nuestro estudio.
A partir del análisis de las revistas a través de la web In-Recs (http://ec3.ugr.es/in-recs/informacion/que-es1.htm), fueron seleccionadas ochenta y nueve revistas. Luego se procedió a la identificación de las revistas con artículos relacionados con el área de geometría. Esta identificación se realizó a través de la Búsqueda Avanzada de Redined (http://www.redined.mec.es/es/informacion.html), siendo ésta una Red de Bases de Datos de Información Educativa: investigaciones, innovaciones, recursos y revistas ibero-americanas sobre Educación, con enlaces al documento en texto completo siempre que esté disponible.
El siguiente paso fue proceder a la revisión y análisis de los artículos, en primer lugar, a través de las revistas físicas de la hemeroteca dependiente de la Biblioteca de la Facultad de Educación y posteriormente en la Biblioteca Virtual de la Universidad de Extremadura. Para la revisión y análisis de los artículos también fue utilizado Dialnet (http://dialnet.unirioja.es/servlet/ayuda_qe) considerada como una hemeroteca virtual, con base de datos de artículos, libros y tesis de contenido fundamentalmente hispano.
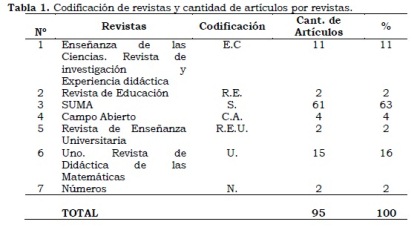
Una vez encontrados los artículos, campo de nuestra investigación, se procedió a darles una estructura y una codificación (Tabla 1). A partir de los artículos y la bibliografía consultada se elaboró una estructura formada por tres clasificaciones, en las que hemos enmarcado los artículos leídos. Estas clasificaciones son: por niveles educativos, por temática correspondiente a cada uno de los niveles educativos y, según materiales y recursos geométricos utilizados en los diferentes niveles educativos.
Las fases seguidas para el análisis de los artículos fueron las siguientes:
1. Lectura de los artículos de una manera global para tener una impresión adecuada de conjunto.
2. Agrupación de los artículos en las distintas clasificaciones construidas en el apartado anterior, teniendo en cuenta el documento de aproximación del paso anterior.
3. Estudio de forma reflexiva cuáles son los contenidos didácticos sobre la geometría en los que inciden los artículos. Se buscó cuál era la tendencia actual sobre la investigación en la enseñanza-aprendizaje de la geometría que se desprende de estas clasificaciones, y qué características comunes encontramos en los artículos correspondientes a un mismo nivel, clase o subclase de las tres clasificaciones definidas.
RESULTADOS Y DISCUSIÓN
Fueron seleccionados 89 revistas de mayor impacto, de las cuales se han identificado 7 revistas de mayor impacto con contenidos relacionados con la geometría, totalizando 95 artículos. De los 95, se logró recopilar un total de 70 artículos. Una vez recopilados, se realizó su lectura buscando una convergencia de las distintas temáticas, que nos permitiera iniciar un análisis más sistemático.
Datos y resultados relativos a Secundaria según los niveles educativos y temáticos.
Atendiendo a la clasificación por niveles educativos, como se puede visualizar en la figura 1, se encontró que las investigaciones realizadas en Educación Secundaria supera ampliamente a los demás niveles con un 48% (70 artículos), seguido por los artículos clasificados en Educación Superior con un 20%.
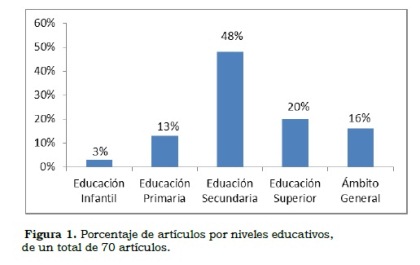
Estos datos indican que el profesorado de la Educación Secundaria es un colectivo interesado en plasmar en artículos sus experiencias e investigaciones, que muestran sus innovaciones y resultados. Este colectivo está preocupado por desarrollar mediante una metodología activa diferentes materiales y recursos que hacen que las actividades realizadas con ellos generen un aprendizaje significativo en los alumnos.
Referente a la clasificación de los artículos por temática correspondiente a cada uno de los niveles educativosen Educación Secundaria, se encontró un 35% para la Geometría Plana, seguido de Geometría espacial y enseñanza-aprendizaje en un 18% (Tabla 2).
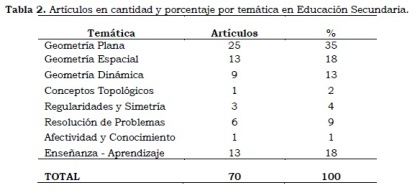
La geometría plana es el tema más tratado en los artículos encontrados en nuestra investigación, un número importante de ellos son artículos relacionados con los fractales. Ordenados estos artículos, podemos partir de Moreno (2002), donde encontramos una introducción a los fractales lineales mediante una experiencia didáctica, en la que se estudia principalmente el diseño y construcción de figuras fractales planas. Este mismo autor, plantea una propuesta de actividades a través del estudio de familias de triángulos y tetraedros fractales de algoritmo lineal común (Moreno, 2003a) e utiliza el juego del caos en la calculadora gráfica para la generación de figuras fractales (Moreno, 2003b).
En el mismo tema, Redondo y Haro (2004, 2005), mediante el análisis en torno al concepto de fractal, ofrecen actividades que intenta adecuar el estudio de este concepto al nivel de secundaria para que el aprendizaje sea más provechoso.
En otro orden de cosas, Gascón (2002) hace un análisis de la presunta alternativa entre la geometría sintética y analítica y se pretende conectar, en la enseñanza de la geometría de secundaria, las técnicas sintéticas con las analíticas para mostrar su complementariedad. También este autor, hace un análisis de las consecuencias didácticas provocadas por la limitación de los temas de las Matemáticas en Secundaria en dos trabajos (Gascón, 2003, 2004).
Dentro de la geometría plana, hay una serie de artículos en los que se presentan actividades muy educativas para Secundaria. Por ejemplo, Ibáñez (2001) a partir de la demostración de un teorema clásico “Los puntos medios de los lados de un romboide definen un rectángulo” sugiere el descubrimiento de otros resultados, es decir, la demostración en Geometría como medio de descubrimiento. Otro artículo, presenta una propiedad del triángulo isósceles, cuya explicación se basa en técnicas y propiedades de la geometría elemental, así como caracterizaciones de estos triángulos (Romero, 2001).
Otros proponen actividades diversas como: analizar la cuadratura de diferentes polígonos regulares (Grupo Alquerque, 2005); el método de Descartes para trazar normales a curvas (Cortés y Calvo, 2004); actividades destinadas a los alumnos que se derivan del Cubo Soma (Grupo Alquerque, 2001); distintas formas de deducción de las fórmulas trigonométricas de suma o resta de ángulos (Munné, 2002); obtener formas geométricas muy recurrentes en el entorno, a partir de octógonos (Fernández y Reyes, 2001); juegos relacionados con el teorema de Pitágoras (Grupo Alquerque, 2003) o una experiencia sobre la aproximación intuitiva en Geometría mediante una aproximación del número (Redondo y Haro, 2002).
Cabe destacar (Pérez, Álvarez y Porta, 2008) en el que se pretende desde un enfoque competencial, despertar en el alumnado el interés por la historia de un problema matemático: la cuadratura del círculo. Este problema puede contribuir a que el alumno adquiera destrezas en el trazado de construcciones gráficas y en el cálculo de las medidas de líneas que las componen. El artículo realiza una breve introducción histórica al problema y se describen las actividades realizadas.
Otro tipo de artículos son aquellos que relacionan la Geometría con otras partes de las Matemáticas, por ejemplo, Ruiz (2001) se pregunta por qué al explicar un concepto matemático no se aprovechan los conocimientos que tienen los alumnos, es decir, al explicar la probabilidad nos olvidamos del área o la longitud.
En la misma línea, Varo, (2000) hace una interpretación geométrica de la regla de los signos para el producto. La necesidad de esta regla radica en la necesidad de que la multiplicación de números positivos y negativos cumpla las mismas propiedades que la multiplicación de números positivos. Sin embargo, Aledo y Cortés, (2001) proponen un buen enfoque geométrico para iniciar a los alumnos en el tema de sumas geométricas de series numéricas como complemento al enfoque analítico-algebraico que se vienen realizando normalmente.
En la temática de Geometría Espacial hemos encontrado trece artículos que también hemos agrupado atendiendo a su similitud en alguna temática.
En un primer grupo, queremos destacar aquellos artículos relacionados con las construcciones, como una manera de tomar contacto con las formas geométricas, pues actualmente muchos profesores de secundaria consideran que la manipulación no es propia de la educación secundaria. Mediante estos trabajos se muestra que dicha manipulación sigue siendo necesaria pero, por supuesto a otros niveles que en la Primaria. Por ejemplo, Rubio (2010) nos presenta una propuesta de actividad docente para la toma de contacto con los poliedros convexos regulares y con el universo de los poliedros en general, con ayuda de modelos modulares de papel plegado diseñados específicamente para dicha actividad. Blanco y otros, (2010) proponen la construcción y el estudio del tetraedro-octaedro y la estrella octángula. También Mora (2002) nos cuenta como se puede construir un omnipoliedro y Fernández y Prieto (2005) deciden realizar el estudio del icosaedro y su construcción a partir de tres rectángulos áureos perpendiculares.
De manera didáctica hay que resaltar el trabajo práctico de Real (2004), que presenta las cónicas como formas geométricas que se pueden generar de múltiples formas y que verifican propiedades que son utilizadas en la vida cotidiana. Sin embargo, Escribano (2000) centra su artículo en tres demostraciones sobre el valor de la potencia de un punto respecto a una circunferencia para suplir el vacío, en los libros de textos de bachillerato.
El siguiente bloque de Secundaria en números de artículos corresponde al de Enseñanza-Aprendizaje en el que se identificaron trece artículos.
A este respecto, Prada (2003) nos ofrece un marco metodológico para la atención a la diversidad dentro del área de Matemáticas. La gran diversidad de alumnos que transitan por las aulas de Educación Secundaria Obligatoria hace necesaria la utilización de metodologías adaptadas a esta realidad. Esta investigación presenta una didáctica, para la enseñanza de la geometría, basada en la utilización de materiales diversificados. Cada uno de los materiales se presenta con una guía para el profesor y una ficha de actividades que va llevando al alumno desde el reconocimiento de las figuras geométricas hasta el razonamiento, siguiendo los niveles de Van Hiele.
No menos interesante es el artículo de Fortuny y Giménez (2001) que trata sobre los razonamientos geométricos de alto nivel y actividades pre-demostrativas con alumnos de doce a dieciséis años. Mediante problemas locales se analizan las nociones y las ideas metodológicas requeridas, para abordar los citados problemas desde el área de la Educación Matemática.
Dentro también de la enseñanza aprendizaje de la geometría, Barrantes (2003) caracteriza la enseñanza-aprendizaje de la geometría indicando los cambios que se han producido en esta enseñanza y que se considera deben ser conocidos por los profesores. Un tema distinto abordan Barrantes y Zapata (2008) cuando reflexionan sobre cuáles son los obstáculos y errores en la enseñanza-aprendizaje de las figuras geométricas que hacen que los alumnos desarrollen esquemas conceptuales incompletos o mal construidos sobre los conceptos, propiedades y clasificación de las figuras geométricas tanto planas como espaciales. Nos ofrecen algunas recomendaciones, basadas en una metodología constructiva, para corregir y erradicar estos obstáculos y errores que impiden una eficaz enseñanza y aprendizaje de las figuras.
Cabe destacar también en Enseñanza-Aprendizaje, los trabajos con papel, de Ledesma (2010), que nos cuenta cómo trabajar en cualquier nivel, distintos contenidos matemáticos, triángulos, cuadriláteros, teorema de Pitágoras, con un simple y sencillo folio de formato DIN-A y varias piezas que se forman con éste y, Mercado (2010) que nos enseña como el mismo docente puede elaborar sus propios materiales didácticos como conos, elipses en conos, triángulos esféricos, el cubo de soma, etc.
Por último, comentar el trabajo de Gorgorió y otros (2000) sobre la reflexión de un grupo de trabajo en el que los profesores de secundaria e investigadores en educación matemática desarrollan actividades geométricas aplicadas a las rotaciones.
Datos y resultados relativos a Secundaria según los materiales y recursos.
En este apartado se han identificado los artículos relacionados a los materiales y recursos, clasificando estos artículos según elementos manipuladores y recursos tecnológicos.
a) Elementos manipuladores
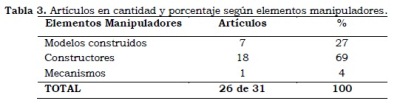
En este bloque se clasifican los artículos que traten algún material concreto, omitiéndose aquellos que de forma general hablan de los materiales o bien hablan en algún apartado de los materiales pero de forma genérica. De esta forma, se encontró 31 artículos que refieren a elementos manipuladores. Estos elementos fueron clasificados en: modelos construidos, constructores y mecanismos. De la clasificación resultante se puede observar que el 69% (18) de los artículos son de la subcategoría de Constructores (Tabla 3), es decir, se utilizan elementos que sirven para hacer modelos diversos o bien para generar situaciones de aprendizaje. El material constructor por excelencia en estos artículos es el papel.
Se puede destacar por su interés el trabajo de Iranzo y Fortuny (2009) en el que se analiza parte de una investigación sobre la interpretación del comportamiento de los estudiantes de Bachillerato Tecnológico en la resolución de problemas de geometría plana, mediante el análisis de la relación entre el uso de GeoGebra, la resolución en lápiz y papel y el pensamiento geométrico. Los autores buscan una relación entre las concepciones de los alumnos y las técnicas que utilizan en las estrategias de resolución de problemas.
Otros autores nos hablan de la utilización del papel para la construcción de elementos geométricos o propiedades (Garrido, 2010; Royo, 2010; Moreira da Costa, 2010) o elaborar materiales didácticos para el aula de matemáticas con papel maché (Mercado, 2010). En estos artículos podemos llegar a construir un omnipoliedro (Mora, 2002); icosaedro y ph (Fernández y Prieto, 2005); elaboración de estrellas (Ramírez, 2005); construcciones con un folio DIN-A (Ledesma López, 2010) y rompecabezas como el tetraedro, octaedro y la estrella octángula (Blanco, Otero y Pedreira, 2010), siempre como materiales aptos para la enseñanza y el aprendizaje en el aula de diferentes contenidos.
Granados, Grau y Nuñez, (2007) trabajan la superficie geométrica, banda de Möbius, como herramienta para potenciar la motivación e interés de los alumnos, tanto de bachillerato como universitarios, en las clases de matemáticas. Mediante papel los alumnos construyen la banda mediante un bucle girado que es manipulable. Una vez elaborado se dan aplicaciones de esta herramienta y utilizando la historia como recurso didáctico se da una breve biografía de August F. Möbius
Con respecto a otros materiales constructores aparece el libro de espejos y sus aplicaciones didácticas (Bermejo, 2002), y artículos del Grupo Alquerque (2003, 2005) que estudia mediante puzle y rompecabezas, y basados en la historia, el Teorema de Pitágoras y la cuadratura de diversos polígonos regulares.
Se han encontrado también un número de artículos sobre Modelos Construidos es decir, aquellos materiales que sirven directamente para observar y concretar conceptos, y profundizar en propiedades. El número de artículo es mucho menor que en la anterior por lo que una clasificación es ya difícil. Por ello comentamos los que consideramos de mayor interés.
Dentro de los artículos referentes a los sólidos, Rubio (2010) nos muestra cómo construir los sólidos plátonicos mediante una propuesta de actividad docente basada en la construcción de módulos de papel que convenientemente engarzados da lugar a dichos sólidos. Guillén (2000), presenta un estudio sobre cuáles son las ideas erróneas de los estudiantes sobre el aprendizaje de conceptos geométricos relativos a los sólidos y el Grupo Alquerque (2001), actividades destinadas a los alumnos que se derivan del Cubo Soma, mediante particiones en éste, se crea el Cubo de Muñoz.
Por último, comentamos el único artículo de la subcategoría “Mecanismos” en el que se utiliza un visor de cónicas. Este trabajo, con alumnos de cuarto de Secundaria, pretende plasmar el estudio de las cónicas como formas geométricas que se pueden generar de múltiples formas y que verifican propiedades que son utilizadas en la vida cotidiana. Las distintas cónicas se generan al cortar un cono con un plano, haciendo variar el ángulo de inclinación del plano con respecto al eje del cono (Real, 2004).
b) Recursos tecnológicos
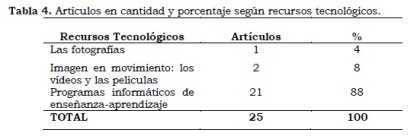
Todos los artículos identificados en este bloque corresponden al de Secundaria. De las cuales el 88% (21) (Tabla 4) pertenecen a Programas Informáticos de Enseñanza-Aprendizaje, que utilizan ordenadores o calculadoras gráficas con diferentes tipos de software para realizar el estudio correspondiente (Lanciano y Camino, 2008; Rizo y Campistrous, 2008; Pérez et al., 2008; Fortuny y Giménez, 2001; Redondo y Haro, 2002; Redondo, 2008).
Pero los artículos realmente interesantes de este apartado son aquellos en los cuales los programas informáticos se utilizan como herramientas para la enseñanza-aprendizaje de la geometría. Por ejemplo, cuando se habla de fractales, también es necesaria la utilización de una calculadora gráfica o un ordenador (Figueiras et al., 2000; Redondo y Haro, 2004; Redondo y Haro, 2005) pero estos artículos no solo nos hablan de los fractales sino que nos muestran como contribuyen a la enseñanza de la geometría.
Así, algunos tienen como base el programa Cabri, tan útil para la enseñanza y el aprendizaje de la geometría, por ejemplo, Pérez Sanz, (2000) que hace una descripción de aplicaciones disponibles en Internet para el programa Cabri-Géomètre, que permite la enseñanza de la geometría de forma más visual. También García y Arriero (2000) utilizan el programa Cabri para el estudio de las cónicas desde dos puntos de vista; la geometría clásica y la geometría analítica. Este artículo concretamente se centra en la elipse y en la parábola.
Mediante Cabri II se intenta también que los estudiantes redescubran los teoremas ya conocidos en Geometría. Se pretende que los estudiantes, habitualmente meros receptores de la información, pasen a trabajar con ella y a desarrollar una creatividad científica. Pichel (2000) nos muestra como el alumno mediante la manipulación de figuras geométricas, como el cuadrado y el triángulo y en torno a los cuales reflexiona, puede llegar a inventar operaciones, estrategias o problemas.
En otra línea, es decir, la formación inicial de profesores de matemáticas de Secundaria tenemos que resaltar trabajos como González y Lupiáñez (2001) que presentan tres actividades: el rotor de Silvester, lecturas de textos y demostraciones, con el objetivo de proporcionar al futuro profesor aspectos específicos de conocimiento profesional relacionados con el uso de software de Geometría Dinámica.
También en (Torregrosa et al., 2010) se analizan las concepciones de los profesores de Secundaria sobre la demostración matemática. Dichas concepciones se manifiestan cuando los profesores participaban en un entorno virtual de aprendizaje. Estos autores describen la influencia que sobre estas concepciones tiene la resolución de problemas de probar usando software dinámico. Por último, Richard (2010) hace un estudio del aporte mutuo de los textos clásicos y la Geometría Dinámica para el aprendizaje de la geometría. Los Élements de géometrie de Alexis Claude Clairaut, publicados por primera vez en 1741, pertenecen a la clase de obras manifiestamente pedagógicas. En este artículo, a partir de una experiencia con alumnos de bachillerato, se muestra cómo se pueden desarrollar sus competencias matemáticas a través de una interpretación del texto de Clairaut y el uso conjunto de software de Geometría Dinámica como es Cabri II Plus.
En la misma línea, Real (2008a, 2008b y 2009) nos presenta tres aplicaciones de software libre relacionada con la geometría. El primero es la presentación de Dr. Geo, una aplicación geométrica libre, que permite el estudio de la geometría plana de una forma interactiva. En el segundo caso nos muestra GTANS, un tangram que combina los puzzles con las figuras geométricas, y por último la aplicación tecnológica denominada Superficies en 3D para el estudio de poliedros, gráficas, superficies de revolución, superficies paramétricas y muchas otras figuras. En todos los artículos encontramos las explicaciones necesarias para el manejo del software como los ejemplos prácticos.
Para el final, hemos dejado dos artículos que relacionan la Informática con la enseñanza-aprendizaje de la geometría de una forma general. En primer lugar, Murillo y Marcos (2009) presentan un modelo para potenciar y analizar el desarrollo de ciertas competencias matemáticas, por parte de alumnos de ESO, cuando desarrollan trabajo colaborativo en un entorno interactivo de aprendizaje que utiliza soportes informáticos. El otro artículo (Gómez, 2010) aborda el estudio de las actitudes de los estudiantes en el aprendizaje de la matemática con tecnología. Este artículo examina las relaciones entre actitudes hacia la matemática y hacia la tecnología. Los resultados dan diferentes sugerencias para la enseñanza y el aprendizaje de la matemática en contextos informáticos y para la evaluación de actitudes.
En el apartado Imágenes y Movimientos y en Fotografías destacamos el trabajo de Thibaut, (2004) que nos cuenta el Proyecto Cube: una introducción a la geometría tridimensional. Dicho proyecto es una propuesta de trabajo en el aula de Matemáticas donde a partir de la película “Cube” se desarrollan una serie de actividades de introducción a la geometría analítica tridimensional y a la visualización espacial geométrica. El proyecto se divide en 2 partes; una relativa al guión de la película y otra derivada dirigida al desarrollo del currículo de cuarto de ESO en geometría. Las características de la propuesta hacen que se presente como un proyecto abierto a la interdisciplinariedad e idóneo para la práctica del aprendizaje significativo en un contexto de prácticas procedimentales.
CONCLUSIONES
Tenemos que destacar el aumento creciente de los trabajos e investigaciones referidas a la Educación Secundaria, lo que indica la preocupación del profesorado sobre la mejora de las enseñanzas y aprendizajes en este nivel educativo.
Esta mejora consideramos, es debido a la creciente calidad de los trabajos presentados en las revistas educativas. Éstas van adquiriendo cada vez un mayor nivel de impacto, es decir, una mayor repercusión en la literatura didáctica, ya que sus artículos son cada vez más citados y por tanto, considerados importantes.
Por otra parte, los materiales constructores o construidos como el papel, espejos, cubo soma, rompecabezas de Pitágoras, vienen a ayudar en el aprendizaje y la enseñanza de los conceptos geométricos y nos muestran que en este nivel de Secundaria también es necesaria la manipulación pero más basada en la exploración y la investigación.
Pero no solamente los materiales, sino que, diferentes actividades y experiencias en las que se enfoca un problema a través de la historia, o donde se habla de construcciones humanas o se relaciona la geometría con la Probabilidad, con el Análisis o el Álgebra, hacen ver la Geometría, no como una ciencia aislada, sino como una herramienta útil y necesaria para el desarrollo de otras partes de las Matemáticas u otras ciencias. En la misma línea, no podemos olvidar que esta materia esta también íntimamente ligada al Arte, en sus distintas manifestaciones como pintura, escultura…
Por otra parte, continúa la creciente importancia que tienen las investigaciones sobre la enseñanza-aprendizaje en formación inicial de profesores de Secundaria. Con respecto a las temáticas se puede concluir la especial importancia que tiene la Geometría Plana y la Geometría Espacial como áreas más tratadas en los artículos de la última década. Dentro de ellas podemos observar que en todos los documentos revisados se tiende hacia una metodología activa, en la que el alumno es el eje de su propio aprendizaje.
A raíz de este trabajo, consideramos que deben seguir surgiendo investigaciones sobre la afectividad y el conocimiento, del tipo de los que analiza las dificultades, esquemas y elementos de lenguaje asociados con las creencias y las actitudes de los profesores acerca de la geometría.
Los medios audiovisuales de comunicación están provocando en los alumnos, y en la sociedad en general, grandes cambios en sus formas de percibir y en sus procesos mentales debido al paso de una cultura escrita a una cultura audiovisual. Destacamos la importancia de los modelos visuales para la adquisición de conceptos geométricos y para fomentar la habilidad de los alumnos a la hora de dar razones lógicas que expliquen y le hagan comprender la validez de las fórmulas geométricas.
Al aprendizaje significativo contribuyen también, los trabajos de la geometría mediante fotografías, películas y sobre todo con programas como Cabri y sus distintas versiones. La principal característica de esta geometría es que su enseñanza es dinámica, es decir, mediante el movimiento y sobretodo, muy visual.
Toda esta tecnología, los materiales, las actividades y las reflexiones que hemos comentado en estos artículos, consideramos que contribuyen al cambio de concepciones en el profesorado hacia la necesidad de implantar, de una vez por todas, una metodología activa pensando en el alumno, y no en los contenidos como tradicionalmente se ha hecho hasta ahora.
REFERENCIAS
Aledo, J.A y Cortés, J. C. (2001). Suma geométrica de series numéricas. Uno: revista de didáctica de las matemáticas, 27, 105-114. [ Links ]
Alsina, C.; Burgués, C. y Fortuny, J. M. (1988). Materiales para construir la Geometría, Madrid, Síntesis. [ Links ]
Barrantes, M. (2003). Caracterización de la enseñanza aprendizaje de la geometría en primaria y secundaria. Campo abierto, 24, 15-36. [ Links ]
Barrantes, M. y Zapata, M. A. (2008). Obstáculos y errores en la enseñanza-aprendizaje de las figuras geométricas. Campo abierto, 27(1), 55-71. [ Links ]
Bermejo, A. (2002). El libro de espejos: aplicaciones didácticas. Suma, 41, 83-92. [ Links ]
Blanco, C.; Otero, T. y Pedreira, A. (2010). Rompecabezas matemáticos en papel: tetraedro, octaedro y estrella octángula. Uno: revista de didáctica de las matemáticas, 53, 92-104. [ Links ]
Calvo, X. (1996). El polydrón, un material que engancha. Uno: revista de didáctica de las matemáticas,7, 19-30. [ Links ]
Cortés, J. C. y Calvo, G. (2004). El método de Descartes para trazar normales a curvas. Suma, 47, 41-46. [ Links ]
Damiani, A. M., Facenda A. M., Fulgenzi, P., Masi, F., Nardi, J. y Paternoster F. (2000). El uso de modelos dinámicos en la Didáctica de las Matemáticas. UNO, 24, 62-79. [ Links ]
Escribano, J. R. (2000). Algunas demostraciones del valor de la potencia de un punto con respecto a una circunferencia. Suma, 35, 71-74. [ Links ]
Fernández, I. y Reyes, M.E. (2001). Construcciones y disecciones del octógono. Suma, 38, 69-72. [ Links ]
Fernández, Á. y Prieto, M. (2005). Icosaedro y ph. Suma, 48, 23-32. [ Links ]
Fernández, M.; Padilla, F.; Santos, A. y Velázquez, F. (1991). Circulando por el círculo, Madrid, Síntesis. [ Links ]
Figueiras, L.; Molero, M.; Salvador, A y Zuasti, N. (2000). Una propuesta metodológica para la enseñanza de la Geometría a través de los fractales. Suma, 35, 45-54. [ Links ]
Fortuny, J. M. y Giménez, J. (2001). Razonamientos geométricos de alto nivel y actividades pre demostrativas con alumnos y alumnas de doce a dieciséis años. Uno: revista de didáctica de las matemáticas, 28, 20-38. [ Links ]
Fortuny, J. M. (1998). Materiales y recursos. Geometría en Primaria y Secundaria. En: Barrantes, M. (ed.) (1998): La Geometría y la Formación del profesorado en Primaria y Secundaria. Badajoz: Servicio de Publicaciones de la Universidad de Extremadura. [ Links ]
García, I. y Arriero, C. (2000). Una experiencia con Cabri: las curvas cónicas. Suma, 34, 73-80. [ Links ]
Garrido, M. B. (2010). Orisangakus: problemas sangaku con papiroflexia como recurso para el estudio de la geometría. Uno: revista de didáctica de las matemáticas, 53, 71-79. [ Links ]
Gascón, J. (2002). Geometría sintética en la ESO y analítica en el Bachillerato: ¿dos mundos completamente separados?. Suma, 39, 5-11. [ Links ]
Gascón, J. (2003). Efectos del autismo temático sobre el estudio de la Geometría en Secundaria I: desaparición escolar de la razón de ser de la geometría. Suma, 44, pp.25-38. [ Links ]
Gascón, J. (2004). Efectos del autismo temático sobre el estudio de la Geometría en Secundaria II: La clasificación de los cuadriláteros convexos. Suma, 45, 41-52. [ Links ]
Gómez, I. M. (2010). Actitudes de los estudiantes en el aprendizaje de la matemática con tecnología. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 28(2), 227-244. [ Links ]
González, M. J. y Lupiáñez J. L. (2001).Formación inicial de profesores de matemáticas de secundaria: actividades basadas en la utilización de software de geometría dinámica. Uno: revista de didáctica de las matemáticas, 28, 110-125. [ Links ]
Gorgorió, N.; Artigues, F. I.; Banyuls, F.; Moyanos, D.; Planas, N.; Roca, M. y Xifré, Á. (2000). Proceso de elaboración de actividades geométricas ricas: un ejemplo, las rotaciones. Suma, 33, 59-71. [ Links ]
Granados, A. B.; Grau, A. y Núñez, J. (2007). La banda de Möbius: un camino que te llevará de cabeza. Suma, 54, 15-22. [ Links ]
Grupo Alquerque (2001). Cubo de Muñoz. Suma, 37, 113-115. [ Links ]
Grupo Alquerque (2003). Rompecabezas del teorema de Pitágoras. Suma, 43, 119-120. [ Links ]
Grupo Alquerque (2005). Cuadraturas de polígonos regulares. Suma, 48, 65-68. [ Links ]
Guillén, G. (2000). Sobre el aprendizaje de conceptos geométricos relativos a los sólidos: ideas erróneas. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 18(1), 35-53. [ Links ]
Hoyos, V. (2006). Funciones complementarias de los artefactos en el aprendizaje de las transformaciones geométricas en la escuela secundaria. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 24(1), 31-42. [ Links ]
Iranzo, N y Fortuny, J. M. (2009). La influencia conjunta del uso de geogebra y lápiz y papel en la adquisición de competencia del alumnado. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 27(3), 433-445. [ Links ]
Ibáñez, M. (2001). Un ejemplo de demostración en Geometría como medio de descubrimiento. Suma, 37, 95-98. [ Links ]
Lanciano, N. y Camino, N. (2008). Del ángulo de la geometría a los ángulos en el cielo: dificultades para la conceptualización de las coordenadas astronómicas acimut y altura. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 26(1), 77-92. [ Links ]
Ledesma, A. (2010). Aventuras y desventuras matemáticas de un folio DIN-A en el instituto. Uno: revista de didáctica de las matemáticas, 53, 45-70. [ Links ]
Mercado, A. I y Custodio, M. Z. (2005). Diseñando camisetas: un viaje por la geometría nazarí. Suma, 49, 33-35. [ Links ]
Mercado, A. I. (2010). Elaboración de materiales didácticos para el aula de matemáticas con papel maché. Uno: revista de didáctica de las matemáticas, 53, 105-111. [ Links ]
Mora, J. A. (2002). Geometría de ayer y de hoy. Suma, 39, 77-82. [ Links ]
Moreira da Costa, E. (2010). Enseñar y aprender matemáticas con origami. Uno: revista de didáctica de las matemáticas, 53, 25-37. [ Links ]
Moreno, J. C. (2002). Experiencia didáctica en Matemáticas: construir y estudiar fractales. Suma, 40, 91-104. [ Links ]
Moreno, J. C. (2003a). Triángulos y tetraedros fractales. Suma, 44, 3-24. [ Links ]
Moreno, J. C. (2003b). El juego del caos en la calculadora gráfica: construcción de fractales. Suma, 42, 69-79. [ Links ]
Munné, J. C. (2002). Distintas formas de deducción de las fórmulas trigonométricas de suma o resta de ángulos. Suma, 39, 33-36. [ Links ]
Murari, C. y Pérez, G. (2001). Caleidoscopios educacionales: coloraciones múltiples. Uno: revista de didáctica de las matemáticas, 27, 7-20. [ Links ]
Murillo, J. y Marcos, G. (2009). Un modelo para potenciar y analizar las competencias geométricas y comunicativas en un entorno interactivo de aprendizaje. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 27(2), 241-256. [ Links ]
Pérez, A. (2001). Cabri e Internet. Suma, 36, 113-115. [ Links ]
Pérez, A. (2002). Geometría visual en Internet. Suma, 41, 125-127. [ Links ]
Pérez, U.; Álvarez, M. y Porta, P. (2008). Historia y enseñanza de la geometría: cuadrando el círculo en el aula. UNO: revista de didáctica de las matemáticas, 49, 111-117. [ Links ]
Pichel, J. M. (2000). Requeteoremas: reiventando teoremas en geometría con Cabri II. Suma, 36, 17-22. [ Links ]
Prada, M. D. de (2003). Marco metodológico para la atención a la diversidad: una experiencia en el área de matemáticas. Revista de educación, 330, 419-447. [ Links ]
Ramírez, R. (2005). Matemáticas en la elaboración de estrellas: demostraciones en cartulinoflexia. Suma, 49, 37-46. [ Links ]
Real, M. (2004). Las cónicas: método de aprendizaje constructivo. Suma, 46, 71-77. [ Links ]
Real, M. (2008a). Dr. Geo: una aplicación geométrica libre. Suma, 58, 75-80. [ Links ]
Real, M. (2008b). Matemáticas lúdicas. Suma, 59, 61-66. [ Links ]
Real, M. (2009). Representación de poliedros y superficies con una aplicación TIC. Suma, 60, 63-71. [ Links ]
Redondo, A. (2008). Los números mórficos en secundaria. Suma, 57, 55-64. [ Links ]
Redondo, A. y Haro, M. J. (2002). Experiencia sobre la aproximación intuitiva en Geometría: una aproximación del número pi en la ESO. Suma, 41, 69-75. [ Links ]
Redondo, A. y Haro, M. J. (2004). Actividades de geometría fractal en el aula de secundaria (I). Suma, 47, 19-28. [ Links ]
Redondo, A. y Haro, M. J. (2005). Actividades de geometría fractal en el aula de secundaria (II). Suma, 48, 15-21. [ Links ]
Richard, P. (2010). Textos clásicos y geometría dinámica: estudio de un aporte mutuo para el aprendizaje de la geometría. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 28(1), 95-112. [ Links ]
Rizo, C. y Campistrous, L. (2008). Una didáctica para el tratamiento de las situaciones de aprendizaje de la geometría con un enfoque dinámico en la escuela. UNO: revista de didáctica de las matemáticas, 49, 73-85. [ Links ]
Romero, J. B. (2010). Una propiedad del triángulo isósceles. Suma, 37, 63-66. [ Links ]
Royo, J. I. (2010). Matemáticas y papiroflexia: una relación bidireccional. Uno: revista de didáctica de las matemáticas, 53, 11-24. [ Links ]
Rubio, J. P. (2010). Descubriendo los sólidos platónicos. Uno: revista de didáctica de las matemáticas, 53, 80-91. [ Links ]
Ruiz, G. (2001). Sobre la utilidad de la Geometría en la enseñanza de la Probabilidad. Suma, 37, 67-74. [ Links ]
Thibaut, E. (2004). Proyecto cube: una introducción a la geometría tridimensional. Suma, 47, 11-18. [ Links ]
Torregrosa, G.; Haro, M. J.; Penalva, M. y Llinares, S. (2010). Concepciones del profesor sobre la prueba y software dinámico: desarrollo de un entorno virtual de aprendizaje. Revista de educación, 352, 379-404. [ Links ]
Varo, A. J. (2000). La regla de los signos. Suma, 34, 69-71. [ Links ]