Introducción
Los clasificadores generativos son modelos que aprenden una probabilidad conjunta P (X, C), definida a partir de las entradas X y la clase C. Estos modelos hacen sus predicciones usando la regla de Bayes para calcular P (C ,X) y luego seleccionan la etiqueta más probable C. En cambio, los clasificadores discriminativos modelan a 𝑃 (𝐶 ,𝑋) directamente, o aprenden un mapeado directamente de las entradas X a las etiquetas de clase C. Existe un mayor número de modelos discriminativos en la literatura que modelos generativos, esto se debe en buena medida a que la obtención de un modelo generativo es una tarea más general que un modelo discriminativo (Ng & Jordan, 2002; Vapnik, 1998). Sin embargo, no existe un consenso de que los modelos discriminativos sean estrictamente mejores que los modelos generativos.
El modelo Naive Bayes es un clasificador generativo muy representativo por la gran cantidad de aplicaciones que posee (Webb et al., 2010), siendo un modelo de gran simplicidad bajo el supuesto de independencia condicional entre cada par de atributos dado el valor de la clase. El modelo de Regresión Logística también es muy representativo para el caso de los clasificadores discriminativos, dada su simplicidad y gran cantidad de aplicaciones (Hilbe, 2009). Por lo tanto, la comparación de la Regresión logística con Naive Bayes es un abordaje empleado para analizar las ventajas y desventajas de la elección de modelos generativos o discriminativos en tareas de clasificación.
La comparación de los modelos Naive Bayes y Regresión Logística ha sido abordada tanto de forma directa donde el objetivo es la comparación, como de forma indirecta donde la comparación solo se realiza para identificar los mejores clasificadores para resolver un problema específico. En cuanto a trabajos cuyo objetivo principal es la comparación de modelos, Ng & Jordan (2002) muestran experimentos donde Naive Bayes tiende a tener menor error de acierto con pocos atributos de entrenamiento, pero que es superado por la regresión logística cuando consideramos el compor tamiento asintótico del error. Sin embargo, existen otras medidas de evaluación de clasificación como precisión, exhaustividad, error absoluto medio, error absoluto medio promedio y medida kappa, donde la regresión logística tiende a ser superior según los conjuntos de datos evaluados por Gladence et al. (2015). En cuanto a comparaciones indirectas de Naive Bayes y Regresión Logística encontramos una mayor cantidad de trabajos, dado que ambos son modelos muy empleados. Se ha identificado que la Regresión Logística tiende a ser superior en las principales métricas de clasificación a Naive Bayes en detección de fraude en tarjetas de crédito (Itoo et al., 2021), clasificación de sentimiento (Prabhat & Khullar, 2017), clasificación de texto (Pranckevičius & Marcinkevičius, 2017), identificación de genotipos de maíz (Seka et al., 2019), detección de cáncer de mama (Sehgal et al., 2012), detección de trastornos de ansiedad (van Eeden et al., 2021), identificación de autoría en texto (Aborisade & Anwar, 2018) y discriminación de eventos sísmicos (Dong et al., 2016). Mientras que no se ha detectado una diferencia tan significativa entre ambos modelos para problemas de predicción de deslizamientos (Nhu et al., 2020), evaluar la necesidad de angiografía coronaria (Golpour et al., 2020), detección de spam (Othman & Din, 2019), detección de diabetes (Utami et al., 2021), clasificación de préstamos (Pundlik, 2016) y predicción de mortalidad por quemaduras (Stylianou et al., 2015). Sin embargo se ha detectado una ventaja significativa de Naive Bayes sobre la Regresión Logística en clasificación de rendimiento académico (Chiok, 2017) y detec ción de fallos en transformadores (Aborisade & Anwar, 2018).
En este trabajo comparamos el desempeño de los algoritmos Naive Bayes y Regresión logística en problemas de clasificación binaria con atributos binarios, donde analizamos la exactitud de ambos clasificadores en función al número de atributos y tamaño de la muestra. Dado que no es fácil conseguir una cantidad significativa de conjuntos de datos reales cumpliendo las características señaladas, se generaron artificialmente 10 distribuciones probabilísticas para cada t = 1, 2, …, 6 atributo binario y a partir de cada distribución se generaron 10 conjuntos de datos de K = 50, 100, 500 instancias. Los conjuntos de datos fueron empleados solamente para entrenar a los modelos. Las distribuciones no fueron consistentes ya que a cada configuración de atributos les puede tocar distintas clases, por lo tanto a la hora de evaluar la exactitud de los modelos se asume que la categoría correcta para una configuración de atributos es la que aparece con más probabilidad. Mientras que lo usual es aproximar el error de clasificación a través de un conjunto de testeo o aplicando validación cruzada, este trabajo calcula el error posibilidades de ocurrencia, entonces el número total de combinaciones será igual a:
n = 𝑖=1 𝑡 𝑛 𝑖 𝑛 𝑐 (1)
Cada valor que puede tomar la variable X será simbolizado mediante xi;j, donde 1 ≤ 𝑗 ≤ 𝑛𝑖.
Dados los atributos X1, X2, …, Xt y la clase C, un patrón consiste en un elemento del conjunto E = X 1 × X 2 × … × Xt × C.
Mientras que una instancia de un conjunto de datos consiste en un patrón perteneciente a un conjunto de datos que fue generado por una distribución probabilística D en E. Con esto, si tenemos t atributos y una clase, entonces la cantidad total de patrones posibles viene dada por la ecuación (1).
Si a cada patrón Pi ∈ E le asignamos un número aleatorio Ni, entonces a cada patrón pi también le podemos asociar una probabilidad Pi de la siguiente manera
P i = N i j=1 n N j (2)
Materiales y Métodos
Nociones preliminares
Consideremos el problema en el que serán estudiados t atributos, los cuales serán representados mediante X1, X2, …, Xt y además, se considera que dichos atributos permiten predecir el valor de la clase C. En este caso, los atributos son considerados como las variables independientes y la clase es la variable dependiente del problema.
Con esto, si consideramos que la variable o atributo Xi posee ni valores posibles de ocurrencia, donde 1≤𝑖 ≤ 𝑡, y la clase C tiene nc donde n representa la cantidad de patrones posibles y viene dada por la ecuación (1).
Notemos que hay n vectores o patrones en E, y cada vector o patrón tiene t + 1 entradas o variables (entre atributos y clases), entonces una manera de representar todos los vectores o patrones posibles es mediante una representación matricial n × (t + 1), donde cada fila puede ser asociada unívocamente con un patrón de E.
El conjunto de distribuciones que es utilizado para la prueba de sensibilidad de los algoritmos es conocido como Distribución Original. Mientras que el conjunto compuesto de datos generados de manera automática y aleatoria, que sirve para el entrenamiento de los algoritmos es conocido como Datos Aleatorios.
Métodos para generación de datos
En esta sección describimos la metodología para obtener los datos de prueba que serán empleados para comparar los modelos Naive Bayes y Regresión Logística. Esta metodología se basa en dos etapas principales i) generar distribuciones sobre atributos y una clase binarios y ii) generar conjuntos de datos a partir de cada distribución obtenida en la etapa previa.
Generación de distribuciones
Para la construcción de la tabla o matriz que representará la Distribución Original seguiremos los siguientes pasos:
Paso 1: Determinar la cantidad de atributos.
Paso 2: Determinar la cantidad de filas y columnas que tendrá la tabla.
Paso 3: Crear la tabla de combinaciones de valores de las variables.
Paso 4: Asignar a cada fila de la tabla de combinaciones posibles un número aleatorio.
Paso 5: Convertir los números aleatorios en probabilidades.
Ejemplo: Consideremos un caso con tres atributos binarios y con una única clase que también sea binaria. Utilizando los siguientes símbolos:
X1:= Atributo 1;
X2:= Atributo 2;
X3:= Atributo 3;
C:= Clase.
Este caso lo podemos presentar con el formato de la Tabla 1.
Tabla 1 Esquema de conjunto de datos para tres atributos y una clase binaria.
| X1 | X2 | X3 | C |
|---|---|---|---|
| 2 opciones | 2 opciones | 2 opciones | 2 opciones |
Como consideramos un caso en el que los atributos y la clase son binarios, es decir que en cada una de ellas tenemos dos opciones de ocurrencia, entonces
n1 = n2 = n3 = nC = 2,
así, si queremos conocer la cantidad total de combinaciones posibles de valores de estas variables, aplicando la ecuación (1), tendremos
n1 · n2 · n3 · nC = 16,
Con esto sabemos que necesitaremos de 16 filas para presentar todas las posibles combinaciones de valores de las variables.
Si consideramos los datos del clima como atributos: la Presión, la Humedad, la Temperatura; y como clase: la Lluvia. Al simbolizar estas variables categóricas tendremos:
X1: = Presión;
X2:= Humedad;
X3:=Temeratura;
C:= Lluvia.
Ahora debemos ver cómo varían las categorías de cada atributo y el de la clase. Así podemos tener la Tabla 2
Tabla 2 Atributos y clases junto a sus posibles valores
| Variables | Valores |
| X1 = Presión | X11= Alta, X12 = Baja |
| X2 =Humedad | X21 = Mínima, X22=Maxima |
| X3 = Temperatura | X31 = Calor, X32 = Frío |
| Clase | Valores |
| C = Lluvia | C11 = Si , C12=No |
Al combinar todas las categorías de las variables entre sí, obtenemos la Tabla 3.
Tabla 3 Tabla con todos los patrones posibles siguiendo el ejemplo
| X1 | X2 | X3 | C |
| Alta | Mínima | Calor | Si |
| Alta | Mínima | Calor | No |
| Alta | Mínima | Frío | Si |
| Alta | Mínima | Frío | No |
| Alta | Máxima | Calor | Si |
| Alta | Máxima | Calor | No |
| Alta | Máxima | Frío | Si |
| Alta | Máxima | Frío | No |
| Baja | Mínima | Calor | Si |
| Baja | Mínima | Calor | No |
| Baja | Mínima | Frío | Si |
| Baja | Mínima | Frío | No |
| Baja | Máxima | Calor | Si |
| Baja | Máxima | Calor | No |
| Baja | Máxima | Frío | Si |
| Baja | Máxima | Frío | No |
Ahora asignamos un número aleatorio a cada patrón, con esto obtenemos la Tabla 4.
Tabla 4. Lista de patrones con los números aleatorios asignados
| X1 | X2 | X3 | C | Ni |
| Alta | Mínima | Calor | Si | 0.02 |
| Alta | Mínima | Calor | No | 0.04 |
| Alta | Mínima | Frío | Si | 0.3 |
| Alta | Mínima | Frío | No | 0.07 |
| Alta | Máxima | Calor | Si | 0.1 |
| Alta | Máxima | Calor | No | 0.08 |
| Alta | Máxima | Frío | Si | 0.21 |
| Alta | Máxima | Frío | No | 0.13 |
| Baja | Mínima | Calor | Si | 0.4 |
| Baja | Mínima | Calor | No | 0.05 |
| Baja | Mínima | Frío | Si | 0.24 |
| Baja | Mínima | Frío | No | 0.38 |
| Baja | Máxima | Calor | Si | 025 |
| Baja | Máxima | Calor | No | 0.58 |
| Baja | Máxima | Frío | Si | 0.7 |
| Baja | Máxima | Frío | No | 0.09 |
Por último, convertimos los números aleatorios en probabilidades, utilizando la ecuación (2), agregamos el número i indicador de fila, obteniendo así la Tabla 5.
Tabla 5. Distribución finalmente generada por la metodología
| i | X1 | X2 | X3 | C | Pi |
| 1 | Al. | Mín. | Calor | Si | 0.00549451 |
| 2 | Al. | Mín. | Calor | No | 0.01098901 |
| 3 | Al. | Mín. | Frío | Si | 0.08241758 |
| 4 | Al. | Mín. | Frío | No | 0.01923077 |
| 5 | Al. | Máx. | Calor | Si | 0.02747253 |
| 6 | Al. | Máx. | Calor | No | 0.02197802 |
| 7 | Al. | Máx. | Frío | Si | 0.05769231 |
| 8 | Al. | Máx. | Frío | No | 0.03571459 |
| 9 | Ba. | Mín. | Calor | Si | 0.10989011 |
| 10 | Ba. | Mín. | Calor | No | 0.01373626 |
| 11 | Ba. | Mín. | Frío | Si | 0.06593407 |
| 12 | Ba. | Mín. | Frío | No | 0.10439560 |
| 13 | Ba. | Máx. | Calor | Si | 0.06868132 |
| 14 | Ba. | Máx. | Calor | No | 0.15934066 |
| 15 | Ba. | Máx. | Frío | Si | 0.19230769 |
| 16 | Ba. | Máx. | Frío | No | 0.02472527 |
Generación de conjuntos de datos
Para la construcción de la tabla con los datos aleatorios necesitaremos definir algunos parámetros. Para decidir si el i-ésimo patrón formará parte de los datos de prueba, tendremos en cuenta la proba bilidad Pi asignada a dicho patrón en la Distribución Original, y la misma será utilizada para definir el rango de valores, el cual estará determinado por un límite inferior LIi y un límite superior LSi. Una vez que tengamos éstos límites podemos utilizar un número aleatorio a producido al azar, éste número a lo compararemos con los límites inferiores y superiores, y al rango al que pertenezca este número aleatorio será el patrón seleccionado para formar parte de los datos de prueba. Generamos a con una distribución uniforme en un rango entre 0 y 1.
Considerando las siguientes notaciones:
i: = posición del patron en la
Distribución Original;
Ri : = rango i;
LIi : = límite inferior del rango i;
LSi : = límite superior del rango i;
Pi : = probabilidad del patrón i;
AcPi: = vector acumulador de probabilidad hasta el patron i.
Podemos definir el vector acumulador de probabilidad como:
Para hallar los límites inferior y superior, consideraremos los siguientes casos:
Para la fila i = 1, consideramos
Para 2≤ 𝐼 ≤ 𝑛−1, consideramos
Para i = n, consideramos
Mientras que el rango del patrón i estará definido como:
Ri = (LIi, LSi). (7)
Es importante tener en cuenta que se ha agregado el vector acumulador de probabilidad para definir los límites inferior y superior de cada rango y entre con lo que estos límites estará ubicado el número aleatorio que se utilizará para seleccionar la instancia. Así, si a es el número aleatorio generado por el programa, entonces buscamos los límites inferior y superior tal que LIi < a ≤ LSi, (8)
La cantidad de filas de la tabla con los datos aleatorios será igual a la cantidad de elementos de la muestra indicada, esto quiere decir que si queremos una muestra con K instancias, entonces la tabla con los datos aleatorios tendrá K filas. Mientras que la cantidad de columnas coincidirá con la cantidad de columnas de la Tabla correspondiente a la Distribución Original. El tamaño de la tabla con los datos aleatorios estará determinado por la cantidad de filas o instancias, ya que la cantidad de columnas será la misma en ambas tablas (en la tabla de Distribución Original y en la tabla con los Datos Aleatorios). Por último, la Distribución Aleatoria será construida siguiendo los siguientes pasos:
Paso 1: Generar un número aleatorio aj (la j indica que es el j-ésimo valor generado).
Paso 2: Verificar en que rango de valores se ubica el número generado: LIi < a ≤ LSi,
donde el valor de i nos indicará la fila en la tabla de la Distribución Original (el patrón) a ser seleccionada.
Ejemplo: Siguiendo con el Ejemplo anterior, lo primero que debemos hacer es presentar la Tabla de la Distribución Original de tal manera que se puedan observar las probabilidades acumuladas. Esta idea es presentada en la Tabla 6.
Supongamos que ya generamos varios valores aj,
Si a1 = 0.54, entonces buscamos el valor de i que verifique
LIi < a1 ≤ LSi
con lo que
LIi < 0.54 ≤ LSi,
lo cual implica que i = 11, ya que 0.54 < 0.55494505 = AcP11.
Tabla 6. Lista de patrones con sus intervalos de selección
| Ditribución Original | AcPi | |||||
|---|---|---|---|---|---|---|
| i | X1 | X2 | X3 | C | Pi | |
| 1 | Al. | Mí. | Calor | Si | 0.00549451 | 0.00549451 |
| 2 | Al. | Mí. | Calor | No | 0.01098901 | 0.01648352 |
| 3 | Al. | Mí. | Frío | Si | 0.08241758 | 0.09890110 |
| 4 | Al. | Mí. | Frío | No | 0.01923077 | 0.11813187 |
| 5 | Al. | Má. | Calor | Si | 0.02747253 | 0.14560440 |
| 6 | Al. | Má. | Calor | No | 0.02197802 | 0.16758242 |
| 7 | Al. | Má. | Frío | Si | 0.05769231 | 0.22527473 |
| 8 | Al. | Má. | Frío | No | 0.03571459 | 0.26098901 |
| 9 | Ba. | Mí. | Calor | Si | 0.10989011 | 0.37087912 |
| 10 | Ba. | Mí. | Calor | No | 0.01373626 | 0.38461538 |
| 11 | Ba. | Mí. | Frío | Si | 0.06593407 | 0.45054945 |
| 12 | Ba. | Mí. | Frío | No | 0.10439560 | 0.55494505 |
| 13 | Ba. | Má. | Calor | Si | 0.06868132 | 0.62362637 |
| 14 | Ba. | Má. | Calor | No | 0.15934066 | 0.78296703 |
| 15 | Ba. | Má. | Frío | Si | 0.19230769 | 0.97527473 |
| 16 | Ba. | Má. | Frío | No | 0.02472527 | 1 |
Con esto, el patrón seleccionado es el presentado en la Tabla 7.
Si a1 = 0.14, entonces i = 11, esto se obtiene siguiendo el procedimiento indicado anteriormente. Con esto, el patrón seleccionado es el presentado en la Tabla 8.
Con estos dos patrones seleccionados formamos la Tabla 9, en la misma se presentan los datos aleatorios.
Tabla 9 Tabla generada con los dos primeros patrones
| X1 | X2 | X3 | C |
|---|---|---|---|
| Baja | Mínima | Frío | Si |
| Alta | Mínima | Frío | No |
Este proceso se debe repetir hasta tener K filas para la tabla de datos aleatorios, la cual se tomará como la muestra de entrenamiento para los algoritmos.
Resultados y discusión
Los algoritmos fueron evaluados en conjuntos de datos de m = 1,2,3,4,5,6 atributos. Para cada m se generaron 10 distribuciones aleatorias y para cada distribución aleatoria se generaron 10 conjuntos de datos de K = 50, 100, …, 500 instancias. En vez de emplear conjuntos de testeo o validación cruzada para estimar el error, este trabajo calcula el error real de los modelos aprovechando que se conoce la distribución real de los datos. Puede notarse también que las distribuciones tienden a producir distintas clases para una misma asignación de valores de los atributos, por lo que si esperamos que el modelo prediga la clase a partir de los atributos siempre existirá un error. Por lo tanto, el cálculo del error de cada modelo se realiza de forma exacta asumiendo que a) la correcta del modelo para cada configuración de atributos es la moda de la clase para tal configuración y b) el tamaño del conjunto de prueba tiende a infinito. Eso se consigue a partir de la siguiente formula
donde i) M (e) es la salida del modelo de clasificación tomando los valores de los atributos del patrón e de entrada, ii) me es la moda de la clase C clasificación se puede calcular como 1 - ε a partir de la ecuación (9).
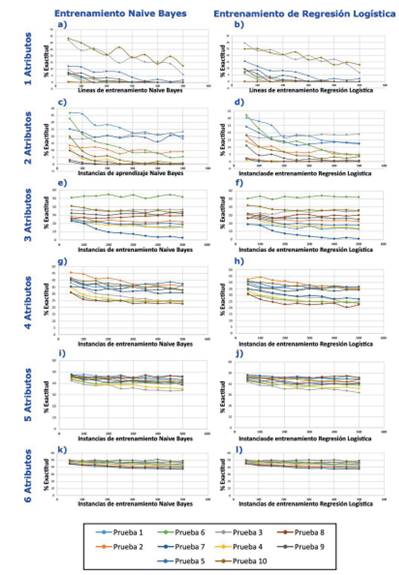
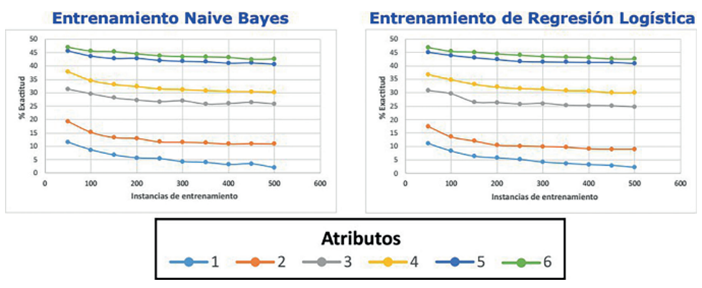
La Figura 1 sumariza los resultados experimentales, donde cada subfigura presenta la exactitud de cada algoritmo aplicado sobre las distribuciones correspondiente a cada número de atributos específico, donde el número atributos crece a medida que bajamos y cada columna de sub-gráficos corresponde a un algoritmo. Los sub- gráficos correspondientes a un mismo número de atributos mantienen el color correspondiente a cada distribución generada, de modo a que se puedan comparar las curvas tanto para Naive Bayes como para la Regresión Logística. Para ambos algoritmos puede notarse como las curvas tienden a descender y acercarse entre sí a medida que crece el número de atributos. También puede notarse como ambos algoritmos se comportan de manera similar para las mismas distribuciones, lo que evidencia que el error no varía proporcionalmente demasiado de un algoritmo a otro. Por lo tanto si una distribución produce más error que otra para un algoritmo, tiende a ocurrir lo mismo en el otro algoritmo, según nuestros experimentos. La Figura 2 presenta la exactitud para cada algoritmo promediando entre las distribuciones generadas para cada número de atributos. Se siguen observando patrones muy similares para ambos algoritmos.
La Tabla 10 presenta la diferencia entre Regresión Logística y Naive Bayes del promedio de exactitud entre las distribuciones de cada número fijo de atributos, en función al número de instancias de entrenamiento. Puede notarse que la diferencia nunca supera 1 y que la mayoría de las veces el valor es positivo, lo que implica que la mayoría de las veces Naive Bayes tuvo un error mayor a la Regresión Logística pero sin superar un 1 %.
Tabla 10. Diferencias de porcentajes de error promedio de predicción de los algoritmos
| Nro. de atributos | Instancias de entrenamiento | |||||||||
| 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | |
| 1 2 | 0.26 1.92 | 0.31 1.74 | 0.36 1.32 | -0.01 2.55 | 0.18 1.49 | 0.08 1.56 | 0.27 1.62 | -0.04 1.76 | 0.50 2.04 | -0.18 1.92 |
| 3 | 0.48 | 0.04 | 1.59 | 1.00 | 0.94 | 1.00 | 0.49 | 0.79 | 1.37 | 1.19 |
| 4 | 1.10 | -0.26 | -0.07 | 0.24 | -0.11 | -0.09 | 0.03 | -0.14 | 0.44 | 0.19 |
| 5 | 0.48 | -0.24 | -0.27 | 0.45 | 0.39 | 0.19 | 0.15 | -0.28 | -0.18 | -0.30 |
| 6 | 0.16 | 0.15 | 0.20 | 0.03 | -0.18 | -0.01 | 0.07 | 0.07 | -0.12 | 0.02 |
Es importante mencionar que la Prueba i no es la misma para cada fila, son pruebas con distintas distribuciones pero numeradas de forma similar por lo que no guardan relación.
Conclusión
Los resultados numéricos no implican que la Regresión Logística sea siempre superior a Naive Bayes. Sin embargo, se ve una leve tendencia a favor de la Regresión Logística y los experimentos donde Naive Bayes supera a la Regresión Logística representan el caso menos común. Estas observaciones siguen la tendencia de los trabajos consultados en la literatura, donde se comparan ambos modelos para solucionar problemas reales. Sin embargo, los experimentos realizados no muestran que el número de instancias revierta de alguna forma la tendencia observada. Esto no se condice con el trabajo de Ng y Jordan, donde se argumenta que el error en Naive Bayes converge más rápidamente a su valor asintótico en función del tamaño de la muestra, aunque la Regresión Logística tendría valores asintóticos menores para el error.
Una ventaja de la Regresión Logística al modelo Naive Bayes representa evidencia importante a favor de los modelos discriminantes, aunque tal diferencia no sea de gran magnitud. Esto se debe a que la Regresión Logística es solo un modelo lineal y por lo tanto está entre los de menor capacidad.
Mientras que Naive Bayes es un modelo muy empleado entre los modelos generativos por la generalidad de sus hipótesis.
Posibles extensiones de este trabajo son:
Extender las pruebas con distribuciones cuyos atributos no sean solo binarios, clasificación multiclase, mayor número de atributos o distribuciones satisfaciendo hipótesis particulares.
Comparación con modelos generativos más sofisticados que Naive Bayes











 uBio
uBio