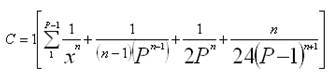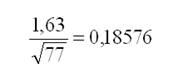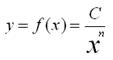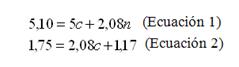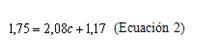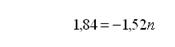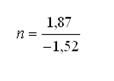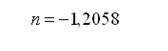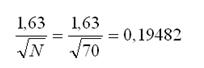INTRODUCCIÓN
La bibliometría como ciencia se basa en el análisis a través del tiempo de los componentes asociados tanto a la generación como al uso de la información científica. Estos elementos se caracterizan por poseer comportamientos que ostentan regularidad estadística, por lo que es factible la definición de los patrones evidenciados mediante las llamadas “leyes” bibliométricas. La denominada “ley” de Lotka es una de las principales de estas leyes1-3.
Por consiguiente, en el marco de este estudio es fundamental partir del trabajo realizado en 1926 por el químico y matemático Alfred James Lotka (1880-1949), quien publica el artículo denominado “The frecuency distribution of scientific productivity”, en el cual describe el análisis realizado a la producción científica de una muestra de autores de química y otra de física4,5. Con este trabajo se establecen las bases para el modelo estadístico del cuadrado inverso, el cual mayormente es conocido como la “ley” de Lotka en honor a su formulador6.
En su trabajo Lotka observó que alrededor del 60% de los autores contaba con una sola contribución, en tanto que los que tenían dos contribuciones eran alrededor del 25% de los que tenían una única contribución7, evidenciándose con esto que la minoría era la responsable de generar la mayor proporción de contribuciones8.
Cabe destacar que tanto el modelo del cuadrado inverso como la forma generalizada del modelo matemático de Lotka han sido aplicados a diversos ámbitos, con el objeto de analizar la productividad de los autores. Se citan a continuación algunos estudios realizados a nivel regional:
-Ajuste del comportamiento de la literatura de jaca al modelo de Lotka9.
-Aplicación del modelo de Lotka a la producción científica latinoamericana en ciencias bibliotecológica y de la información5.
-Comprobación del ajuste de la productividad científica estudiada por Oliveira a la ley de Lotka por el método del poder inverso generalizado10.
-Evaluación del ajuste de la productividad de los autores de literatura sobre plantas medicinales del Perú a la ley de Lotka11.
-Aplicación del modelo del poder inverso generalizado a la productividad de los autores en la ciencia de la información colombiana12.
-Estudio de re-evaluación de la productividad de los autores sobre la literatura del péndulo publicada desde 1629 a 1885, en el cual se aplican los modelos del cuadrado inverso y poder inverso generalizado7 .
En este contexto se plantea una investigación sobre la productividad científica de los investigadores del área de Ciencias Médicas y de la Salud categorizados en el Programa Nacional de Incentivo a los Investigadores (PRONII) del Consejo Nacional de Ciencia y Tecnología (CONACYT) de Paraguay, que al año 2016 se encuentran activos o asociados. A este respecto es significativo señalar que el investigador es definido como un profesional que concibe nuevos conocimientos, productos, procesos, métodos y/o sistemas a través de trabajos de investigación en cualquiera de las áreas de la ciencia(13, 14).
En efecto, el CONACYT por intermedio del PRONII lleva a cabo la categorización de investigadores para otorgamiento de incentivos económicos, mediante procesos de valoración que contemplan su influencia en la instrucción de otros investigadores, su trascendencia fuera del país y su productividad científica(15, 16).
En el PRONII se establecen17:
-Áreas del Conocimiento: Ciencias Exactas y Naturales, Ingeniería y Tecnología, Medicina y Ciencias de la Salud, Ciencias Agropecuarias, Ciencias Sociales, Humanidades.
-Categorías: Investigadores Activos, Investigadores Asociados e Investigadores Eméritos.
-Niveles: Candidato a Investigador, Nivel I, Nivel II y Nivel III. Cabe aclarar que la categoría “Investigador Emérito” no corresponde a nivel alguno.
Es así que la relevancia de la presente investigación radica en que la misma plantea el estudio del comportamiento de la productividad científica de los investigadores del área de Ciencias Médicas y de la Salud categorizados en el PRONII, mediante la aplicación de uno de los modelos matemáticos más relevantes en el campo de la bibliometría: el modelo matemático de Lotka. Consecuentemente se establece como objetivo de este trabajo la comprobación del ajuste del comportamiento de la productividad científica de los investigadores del área de Ciencias Médicas y de la Salud que se encuentran categorizados al año 2016 en el PRONII, al postulado teórico del modelo matemático de Lotka.
MATERIALES Y MÉTODOS
Se planteó un estudio con enfoque cuantitativo, con alcance descriptivo correlacional, y de corte transversal18.
En lo que respecta a la población de estudio es preciso señalar que se ha procedido a la conformación de una base de datos de investigadores categorizados en el PRONII, pertenecientes al área de Ciencias Médicas y de la Salud, en el período 2011-2016. Para tal efecto se recurrió a las resoluciones del CONACYT19-22, en las cuales se establecen las nóminas de categorizados, correspondientes a las convocatorias 2011, 2013, 2015 y 2016. Se realizó este procedimiento a fin de establecer la nómina de investigadores con categoría activo o asociado al año 2016.
Posteriormente se llevó a cabo, entre los meses de marzo y abril del año 2018, la búsqueda de las publicaciones (contribuciones) alojadas en la Web of Science de los investigadores del área de Ciencias Médicas y de la Salud con categoría activo o asociado al año 2016. Es preciso señalar que en este estudio se consideraron las publicaciones generadas por los investigadores a lo largo de su vida, disponibles hasta la fecha mencionada en la base de datos referida. Asimismo, es de destacar que solo se ha incluido como población objeto de estudio a los investigadores activos o asociados debido a que interesa el comportamiento de la productividad de aquellos que se encuentran sujetos a los procesos de evaluación periódica propios del PRONII, en los cuales la producción científica resulta preponderante tanto para el ingreso como para la permanencia en el programa.
El acceso a la Web of Science se realizó a través del Centro de Información Científica del CONACYT (CICCO)23, efectuándose la búsqueda de las publicaciones en las bases de datos siguientes a las cuales el CONACYT poseía suscripción:
-Colección principal de Web of Science (Science Citation Index Expanded, Social Sciences Citation Index, Arts & Humanities Citation Index, Emerging Sources Citation Index)
-KCI - Korean Journal Databse
-Russian Science Citation Index
-SciELO Citation Index
En la búsqueda de las publicaciones se utilizaron los criterios siguientes:
-Nombres y apellidos del autor
-Refinado de los resultados por país “Paraguay”
Se incluyó en el recuento sólo las publicaciones en las que el investigador:
-Posee filiación a una institución perteneciente a Paraguay
-Se encuentra como primer autor. En este trabajo se aplicó el criterio de primera autoría para realizar el conteo de contribuciones por autor tal como lo hicieron Lotka4, Gorbea Portal5) y otros autores en sus estudios.
Ahora bien, en lo que concierne al modelo aplicado en el presente estudio cabe mencionar que Urbizagástegui expone que esta llamada “ley” de Lotka o modelo matemático de Lotka describe el comportamiento de la productividad de autores dentro de una determinada área de la ciencia y dentro de un lapso específico, con base en una distribución de probabilidades discretas(10, 24).
En este sentido es significativo resaltar que según el modelo matemático de Lotka, o modelo del cuadrado inverso, la cantidad de autores que poseen “x” contribuciones en un área de la ciencia es alrededor de 1/x2 el de los autores que poseen una única contribución5,11. De esto se deduce que las contribuciones hechas por los autores presentan una distribución desigual, aglomerándose la mayor proporción de las contribuciones en unos pocos autores, los cuales con respecto a los autores de menor aporte de contribuciones presentan una relación negativa de alrededor de 224.
Además, es pertinente subrayar que existe una forma generalizada del modelo de Lotka, conocido como modelo del poder inverso generalizado, el cual se expresa de la siguiente manera24:
Por otra parte, en lo que hace a la metodología para comprobar el modelo refiere Gorbea Portal que fue Pao quien realizó los aportes más relevantes en cuanto a la comprensión del modelo de Lotka, planteando la pertinencia de calcular el valor del exponente “n” a partir de los datos correspondientes a la muestra estudiada, en los casos en que el valor de n igual a 2 no resulte acorde a la muestra analizada5. Es así que como producto de su estudio Pao sugiere una serie de pasos a seguir para realizar la comprobación del modelo de Lotka, siendo éstos25: a) En la recopilación de los datos deben considerarse las contribuciones de los autores en un ámbito determinado de la ciencia, acreditándose la contribución solo al primer autor. b) Los datos deben tabularse de tal manera que en la primera columna se disponga en forma descendente la cantidad de contribuciones “x”, y en la segunda, la cantidad de autores que realizan “x” contribuciones. c) Debe utilizarse el método de mínimos cuadrados para realizar el cálculo del valor de “n” ajustado a los datos observados, aplicándose la fórmula siguiente:
 Dónde: X: Logaritmo de base 10 de x Y: Logaritmo de base 10 de y N: Cantidad de pares de datos en la muestra
Dónde: X: Logaritmo de base 10 de x Y: Logaritmo de base 10 de y N: Cantidad de pares de datos en la muestrad) Debe calcularse el valor del parámetro “C” a partir del valor de “n” ajustado a los datos estudiados, conforme a la fórmula que se da a continuación:
A este respecto es necesario señalar que en la aplicación del modelo de Lotka en el presente estudio se consideró: a) El estadístico de prueba de Kolmogorov-Smirnov (K-S) para la comprobación estadística del modelo, a un nivel de significación del 1%. b) El método de mínimos cuadrados para el cálculo del valor de “n” ajustado a los datos estudiados. c) El valor de “C” como la cantidad de investigadores que generan una única publicación, correspondiendo este valor a la cifra absoluta observada en la muestra, la cual se utilizó como pivote para el cálculo de los valores restantes5.
Por último, es sumamente importante destacar que en este trabajo se consideró como referencia principal el estudio realizado por Gorbea Portal en el 2005, denominado “El modelo matemático de Lotka: su aplicación a la producción científica latinoamericana en ciencias bibliotecológica y de la información”5.
RESULTADOS
En cuanto a los resultados obtenidos, es de mencionar que se ha establecido para este estudio un total de 159 investigadores del área de Ciencias Médicas y de la Salud categorizados en el PRONII, activos o asociados al año 2016, considerándose las convocatorias de los años 2011, 2013, 2015 y 2016, siendo ésta la población con respecto a la cual se realizó la búsqueda de publicaciones en la Web of Science.
Se apreció que del total de 159 investigadores alrededor de la mitad no poseían publicaciones en la Web of Science, en las cuales se encuentren como primer autor con filiación a una institución de Paraguay. En contrapartida, cerca del 35% posee entre 1 y 3 publicaciones (Tabla 1).
Tabla 1: Distribución de investigadores según cantidad de publicaciones
| Cantidad de publicaciones | Cantidad de investigadores |
|---|---|
| Total | 159 |
| Ninguna publicación | 82 |
| 1 publicación | 29 |
| 2 a 3 publicaciones | 26 |
| 4 a 5 publicaciones | 15 |
| 6 y más publicaciones | 7 |
Con referencia a la distribución de los investigadores con al menos una contribución, de acuerdo a la cantidad de publicaciones, como es de esperarse, la frecuencia de la cantidad de investigadores disminuye conforme aumenta la cantidad de publicaciones. Se observó que del total de 77 investigadores que poseen por lo menos una publicación, cerca del 38% ha generado una única contribución (Tabla 2).
Tabla 2: Distribución de investigadores con al menos una publicación, según cantidad de publicaciones
| Cantidad de publicaciones | Cantidad de investigadores |
|---|---|
| Total | 77 |
| 1 publicación | 29 |
| 2 publicaciones | 20 |
| 3 publicaciones | 6 |
| 4 publicaciones | 12 |
| 5 publicaciones | 3 |
| 7 publicaciones | 6 |
| 44 publicaciones | 1 |
De aquí que, el modelo matemático de Lotka C/x2 se aplicó a un total de 236 publicaciones generadas por 77 investigadores (Tabla 3). Se utilizó el estadístico de prueba de Kolmogorov-Smirnov (K-S), a un nivel de significación de 1%, para comprobar el ajuste de los datos observados a los esperados según el modelo de Lotka. Los resultados obtenidos se dan en la siguiente tabla:
Tabla 3: Distribución de investigadores según cantidad de publicaciones y comprobación estadística del modelo matemático de Lotka
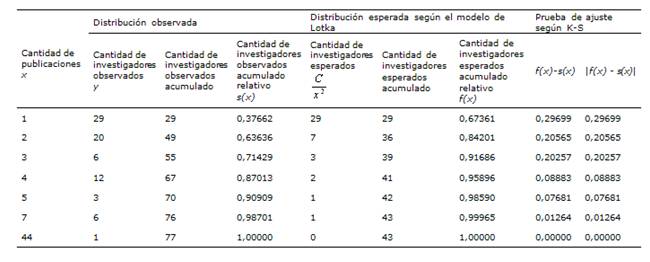
La distancia máxima encontrada entre la distribución relativa acumulada de investigadores observados y esperados, es decir la distancia máxima calculada, fue de 0,29699 (Tabla 3).
En la representación gráfica de la productividad de investigadores se denota que no se presentó un buen ajuste entre la curva proveniente de los datos observados y los esperados conforme al modelo matemático de Lotka (Figura 1).
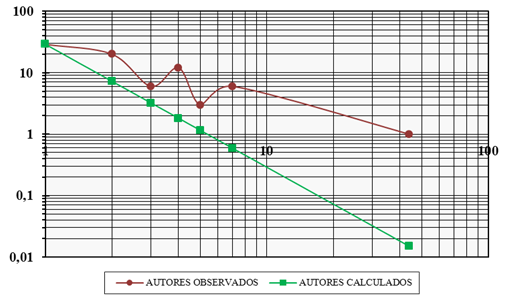
Figura 1: Distribución de la productividad de los investigadores observados y esperados según el modelo matemático de Lotka (escala logarítmica)
Por otra parte, para la determinación del valor crítico de la prueba de Kolmogorov-Smirnov, a un nivel de significación de 1% (α=0,01) se aplicó 1,63/√N, siendo “N” la cantidad total de investigadores observados. El resultado obtenido se detalla a continuación:
Al realizar la comparación entre valor crítico y la máxima desviación absoluta calculada, para determinar si se acepta o no la hipótesis nula planteada en este estudio, en la cual se sostiene que “La productividad científica de los investigadores activos o asociados del área de Ciencias Médicas y de la Salud, categorizados en el PRONII al año 2016, cumple con el modelo matemático de Lotka”, se aplicó el siguiente criterio de decisión determinado por Kolmogorov-Smirnov en su prueba:
-Si el valor crítico es mayor o igual a la máxima desviación absoluta calculada, la hipótesis nula no se rechaza.
-Si el valor crítico es menor a la máxima desviación absoluta calculada, la hipótesis nula se rechaza.
Comparando los valores correspondientes a la máxima desviación absoluta calculada y el valor crítico del estimador para α=0,01 se obtuvo que:
Dmáx=0,29699>Valor crítico=0,18576
Como el valor crítico es menor a la máxima desviación absoluta calculada, la hipótesis nula se rechazó. Por lo tanto, se comprobó que la productividad de los investigadores observados no se ajusta al modelo matemático propuesto por Lotka.
Esto motivó la comprobación del modelo en un subconjunto de la población, aplicándose un corte a los datos, tal como lo realizó Gorbea Portal5 en su estudio. Asimismo, se llevó a cabo el cálculo del valor que para esta muestra pudiera adoptar el exponente “n”, a través del método de los mínimos cuadrados, tal como refiere Pao25.
De esta manera, a la totalidad de los datos (6 pares ordenados) se aplicó un corte mediante los procedimientos que se mencionan a continuación5:
-Eliminación de la raíz cuadrada de la cantidad total de investigadores observados
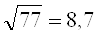
-Eliminación de la raíz cuadrada del total de investigadores con una única publicación
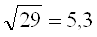
En el primer caso, la decisión sería eliminar cerca de 9 investigadores y en el segundo alrededor de 5, considerando a los investigadores con mayor productividad. A partir de esto se decidió considerar la cantidad de publicaciones hasta el valor 5. A esta muestra se aplicó la forma generalizada del modelo de Lotka, denominado modelo del poder inverso generalizado, dado por:
Para lo cual se llevó a cabo el cálculo del valor de “n” ajustado a los datos de la muestra, utilizándose las siguientes ecuaciones5:
Las sumas totales requeridas en las ecuaciones anteriores se presentan en el cuadro siguiente:
Tabla 4: Sumas totales para el cálculo del valor de "n" ajustado a los datos muestrales
| Cantidad de publicaciones | x 2 | Cantidad de investigadores observados | logy | logx | logy.logx | (logx) 2 |
| x | y | |||||
| 1 | 1 | 29 | 1,46 | - | - | - |
| 2 | 4 | 20 | 1,3 | 0,3 | 0,39 | 0,09 |
| 3 | 9 | 6 | 0,78 | 0,48 | 0,37 | 0,23 |
| 4 | 16 | 12 | 1,08 | 0,6 | 0,65 | 0,36 |
| 5 | 25 | 3 | 0,48 | 0,7 | 0,33 | 0,49 |
| ∑=15 | ∑=55 | ∑=70 | ∑=5,10 | ∑=2,08 | ∑=1,75 | ∑=1,17 |
Reemplazados los valores de las sumas totales obtenidas en las ecuaciones descriptas anteriormente se obtuvo:
Cabe aclarar que los cálculos se realizaron con la totalidad de los valores decimales.
Para llevar a cabo la resolución del sistema de ecuaciones se procedió a:
Luego de realizar la sumatoria de la primera y segunda ecuación se obtuvo:
A través de este procedimiento se obtuvo el siguiente valor para “n”:
Con el valor de “n” calculado para los datos de la muestra se procedió a aplicar a los datos recortados el modelo de Lotka en su forma generalizada. Posteriormente se utilizó nuevamente la prueba de Kolmogorov-Smirnov, a un nivel de significación de 1%, para comprobar el ajuste del modelo a los datos observados.
Los resultados obtenidos se presentan a continuación:
Tabla 5: Distribución de investigadores según cantidad de publicaciones y comprobación estadística de la forma generalizada del modelo matemático de Lotka en la muestra
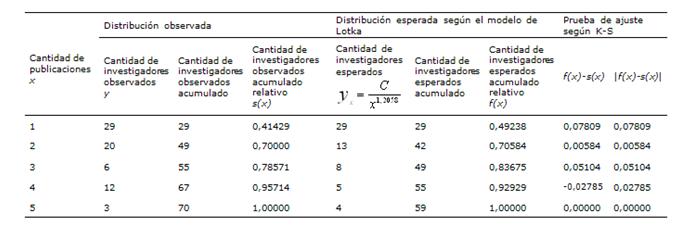
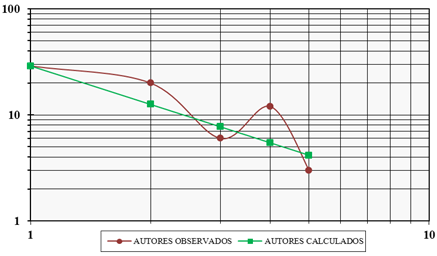
La distribución de la productividad de los investigadores observados y los esperados según la forma generalizada del modelo matemático de Lotka se presenta en la Figura 2.
La distancia máxima calculada para los datos de la muestra fue de 0,07809; mientras que el cálculo del valor crítico del estimador, a un nivel de significación de 1% (α=0,01), arrojó un valor de:
La comparación de la máxima desviación absoluta y el valor crítico del estimador para α=0,01 dio como resultado: Dmáx=0,07809<Valor crítico=0,19482
Debido a que la máxima desviación absoluta es menor al valor crítico la hipótesis nula no se rechazó. Por consiguiente, se comprobó que la productividad de los investigadores observados en la muestra se ajusta a la forma generalizada del modelo matemático de Lotka.
DISCUSIÓN
El presente estudio permitió describir la relación existente entre los investigadores del área de Ciencias Médicas y de la Salud categorizados en el PRONII y su productividad científica.
Los hallazgos permiten apreciar que a través de cuatro convocatorias realizadas (2011, 2013, 2015, 2016) el PRONII cuenta con un total de 159 investigadores categorizados pertenecientes al área de Ciencias Médicas y de la Salud, que se encuentran activos o asociados al año 2016. Este resultado condice con los datos publicados en el Informe de Gestión del año 2017 del Consejo Nacional de Ciencia y Tecnología26.
Los resultados muestran que en torno al 50% de los investigadores no poseen publicaciones en la Web of Science en las cuales se figuren como primer autor y con filiación a una institución de Paraguay. En este estudio no se ahonda en los factores que podrían explicar este hecho, pero puede suponerse que podría deberse al sesgo inherente a la base de datos seleccionada para la realización de la búsqueda de contribuciones, a la baja productividad de los investigadores filiados a instituciones paraguayas y/o a la participación de éstos mayormente como coautores en las publicaciones que como primer autor o autor principal. La determinación de los factores que pudieran explicar en mayor medida este hecho queda como cuenta pendiente de este estudio, pero genera un tema que podría ser abordado en otras investigaciones.
Por otro lado, se aprecia que 77 investigadores poseen una o más publicaciones. En este contexto resulta particularmente llamativo el hecho de que un único investigador posee 44 publicaciones, valor que se aleja notablemente del inmediatamente anterior que es el de 7 publicaciones generadas por 6 investigadores. Esto ameritaría un estudio a profundidad a fin de caracterizar al grupo de investigadores más productivos.
A las 236 publicaciones generadas por estos 77 investigadores se aplicó el modelo matemático de Lotka C/x2, realizándose la comprobación del ajuste de los datos observados a los esperados según el modelo mediante el estadístico de prueba de Kolmogorov-Smirnov a 1% de nivel de significación. Esta prueba evidenció que la productividad de los investigadores observados no se ajusta al modelo propuesto por Lotka. Este resultado podría explicarse considerando que en el presente estudio sólo el 38% de los investigadores posee una única publicación, en tanto que en el trabajo realizado por Lotka este valor asciende a aproximadamente 60%4. Además, no debe perderse de vista la presencia de un investigador con 44 publicaciones, valor que podría influir en el ajuste de los datos observados a los esperados según el modelo de Lotka.Complementando, cabe mencionar que Gorbea Portal halló en su estudio que de la totalidad de autores analizados alrededor del 73% contaba con una sola contribución y comprobó el no ajuste de los datos al modelo propuesto por Lotka5. De la misma forma Restrepo Arango y Urbizagástegui Alvarado encontraron que el 74% de los autores estudiados produjeron un solo documento y rechazaron el ajuste de los datos al modelo del cuadrado inverso7. De manera que en el presente estudio, al igual que en los otros dos mencionados, la proporción de autores que produce un solo trabajo se aleja sustancialmente del valor encontrado por Lotka y se ha concluido que los datos observados no se ajustan al modelo del cuadrado inverso.
Ante la comprobación del no ajuste de la totalidad de datos observados al modelo se determinó seleccionar una muestra de 70 investigadores (investigadores que cuentan con hasta 5 publicaciones) del total de 77 analizados en un primer momento.
Se procedió entonces a aplicar la forma general del modelo de Lotka yx=C/xn a un total de 150 publicaciones generadas por los 70 investigadores seleccionados, con el correspondiente cálculo del valor de “n” ajustado a los datos de la muestra, obteniéndose un valor negativo de alrededor de 1,2058; a diferencia de lo encontrado por Lotka en su trabajo en el que se presenta una relación negativa de aproximadamente 224. En contrapartida, Urbizagastegui Alvarado10 establece en su estudio n= -2,14, y análogamente Gorbea Portal5 determina en su muestra recortada n= -2,3141.
Se utilizó nuevamente la prueba de Kolmogorov-Smirnov para comprobar el ajuste de los datos muestrales observados al modelo. Con esta prueba se confirmó que la productividad de los investigadores de la muestra se ajusta a la forma generalizada del modelo de Lotka, a un nivel de significación de 1%.
De este modo se comprueba que el comportamiento de la productividad científica de la muestra de investigadores del área de Ciencias Médicas y de la Salud categorizados se ajusta al modelo matemático de Lotka en su forma generalizada, siendo éste uno de los modelos de mayor relevancia en el ámbito de la bibliometría. Asimismo se establece que el modelo acorde a los datos muestrales se expresa como yx=C/x1,2058.
Además, es significativo señalar que a pesar del ajuste de los datos muestrales a los esperados según la forma generalizada del modelo de Lotka, solo alrededor del 40% de los investigadores muestreados posee una sola publicación. Esta proporción se acerca más a la encontrada por Lotka4, pero aún resulta ser menor. Esto podría deberse a que la producción científica constituye uno de los aspectos evaluados por parte del PRONII tanto para el ingreso como la para permanencia de los investigadores en el programa, aunque no necesariamente en las condiciones que en este estudio se explicita debieran tener las publicaciones para ser consideradas dentro del conteo de contribuciones por investigador.
Es así que con los hallazgos obtenidos en este estudio podría presumirse que la existencia de autores ocasionales es limitada y más bien suponerse que los investigadores se encuentran abocados a la generación de publicaciones científicas.
Por otra parte, es de vital importancia hacer referencia a las limitaciones de la presente investigación inherentes a la elección de la población a la cual se ha aplicado el modelo de Lotka, ya que se ha incluido únicamente a los investigadores categorizados en el PRONII, y no así a los no categorizados pero que pertenecen igualmente al área de Ciencias Médicas y de la Salud, lo cual podría suponer cierto sesgo ya que se consideró solo a los investigadores que cumplen con los estándares para pertenecer al PRONII, investigadores que cuentan con trayectoria, y no a los que se encuentran en el campo de la investigación pero de manera más incipiente, o que no cumplen con todos los requerimientos para categorizar. Esta situación podría dar la explicación al hecho de que la cantidad de publicaciones se aglomera entre 1 y 2, y no se concentra en la publicación única como se observa en otros estudios.
En esta línea de ideas, otra cuestión no menos importante es que se asignó la publicación solo al primer autor, criterio bastante utilizado dentro de la comprobación del modelo, que fue el método de conteo de contribuciones por autor aplicado por el mismo Lotka. Sin embargo, a este respecto debe tenerse en cuenta que en el área de Ciencias Médicas y de la Salud se da la particularidad, no así en otras ciencias, de que el autor correspondiente posee prácticamente la misma relevancia que el primer autor. Los investigadores del área de Ciencias Médicas y de la Salud categorizados en el PRONII no están exentos de esta situación, tal es así que los investigadores de mayor nivel de categorización tienden a aparecer como autor correspondiente y no como primer autor.
De igual manera es significativo hacer referencia a la limitación que conlleva haber utilizado la Web of Science para realizar la búsqueda de las publicaciones, en atención a que existen revistas regionales y nacionales que no se encuentran disponibles en la citada base de datos y que podrían albergar publicaciones generadas por los investigadores considerados en este trabajo.
Por lo expuesto se propone que en futuros estudios en esta línea de investigación se considere la productividad científica tanto de los investigadores categorizados como no categorizados, a fin de reducir posibles sesgos provenientes de la selección de la población objeto de estudio. Asimismo, se recomienda la aplicación del criterio de “autor correspondiente” para realizar el conteo de las publicaciones de los investigadores del área de Ciencias Médicas y de la Salud. Igualmente se sugiere la utilización de bases de datos que contemplen revistas regionales y nacionales de manera a disponer de una cuantificación más amplia de la productividad científica. La consideración de los puntos referidos aportaría significativamente a profundizar el análisis y la comprensión del comportamiento de la productividad científica de los investigadores del área de Ciencias Médicas y de la Salud.
Otro punto interesante a ser tomado en cuenta como variante en la comprobación del modelo de Lotka en próximos estudios lo constituye la utilización de otros estadísticos de prueba.
A partir de las conclusiones obtenidas en este trabajo se propone dar continuidad a la línea de investigación abordada con otros estudios que impliquen la comprobación del modelo de Lotka en el área de Ciencias Médicas y de Salud, considerándose en la comprobación del mismo variantes como: el estadístico de prueba, el método de conteo de contribuciones por autor, la base de datos de referencia, por citar algunas. Igualmente, sería de suma relevancia que en estudios posteriores pudiera abordarse el análisis de factores de contexto, como la formación académica, características laborales, entre otras; a fin identificar aquellos que explican en mayor medida el patrón de comportamiento de la productividad científica observado en la presente investigación. Asimismo, la comprobación del modelo de Lotka en otras áreas de la ciencia constituiría un gran aporte al campo de la bibliometría.
Finalmente, es de destacar que la relevancia de los resultados alcanzados en este trabajo radica en que muestran el comportamiento del relacionamiento entre los investigadores del área de Ciencias Médicas y de la Salud categorizados en el PRONII y su productividad científica. Además, el modelo establecido a partir de los datos observados en la muestra ofrece la posibilidad de predecir, dadas ciertas condiciones, la cantidad de investigadores con determinada cifra de publicaciones.