INTRODUCCIÓN
Los maestros son el factor principal para que un aprendizaje matemático de calidad sea posible en la escuela, son los protagonistas y gestores centrales en las acciones y hechos dados en el aula escolar, y este postulado está muy bien remarcado en el informe de la UNESCO (2012), y de la OCDE (2005). De ahí que autores como Bass (2007), Spangler (2014) y Rojas González (2014), han referido que las investigaciones en estos últimos años se han centrado en qué y cómo los maestros abordan el contenido que enseñan, pues estos fenómenos son centrales para la eficacia de la educación matemática escolar de calidad.
La literatura en torno al maestro de matemáticas escolar hoy es muy nutrida, se celebran foros, seminarios, congresos sobre el tema, así por ejemplo anualmente se lleva a cabo por el International Group for the Psychology of Mathematics Education (PME) un gran encuentro de investigadores; del encuentro en Grecia (2009) surgieron tres perspectivas o líneas de investigación, así la llevada por Ball, Thames y Phelps, 2008: Conocimiento Matemático para Profesores (Mathematical knowledge for Teaching),Rowland, Huckstep y Thwaites, 2005: Cuatriada del Conocimiento (Knowledge Quartet) y Davis y Simmt, 2006: Matemáticas para profesores (Mathematics for teaching), son las corrientes más seguidas y desarrolladas en la actualidad.
En lo que se refiere a investigaciones sobre expertizaje docente en matemáticas se toma como marco lo siguiente:
“Los docentes expertos en matemáticas tienen profundo conocimiento de la materia en el nivel que enseñan; identifican apropiadamente los aspectos que conllevan dificultades a los estudiantes, ponen énfasis en el desarrollo del pensamiento y habilidades matemáticas de los alumnos, usan la resolución de problemas matemáticos para la mejora efectiva de la instrucción, centran la instrucción en el estudiante y motivan a sus alumnos” (Rojas González, 2014, p. 22).
Atendiendo al contexto líneas atrás expuesta, y teniendo a mano los resultados del Tercer Estudio Regional Comparativo y Explicativo (TERCE), realizado por la Oficina Regional de Educación de la UNESCO para América Latina y el Caribe (OREALC) con sede en Santiago de Chile, que evalúan a Paraguay, entre otros países de la región, en esta investigación se plantea ¿Los docentes del 3º grado de la Educación Escolar Básica en el Paraguay, con capacitación continua son más eficaces que los que no poseen capacitación continua? (UNESCO-OREALC, 2016).
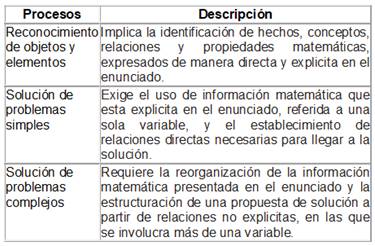
Así se tiene que el TERCE divide el área de Matemáticas por dominios conceptuales y procesos (Tabla 1). Los objetivos específicos de los procesos, se detalla en la Tabla 2.
Tabla 1: Área de Matemáticas, según TERCE, por dominios conceptuales y procesos.
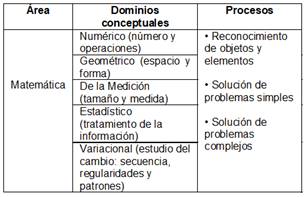
Fuente: Flotts et al., 2016, p. 53.
En cuanto al desempeño de los escolares, según su performance los clasificados por niveles, se presenta en la Tabla 3.
Tabla 3: Desempeño de los escolares, según su performance clasificados por niveles.
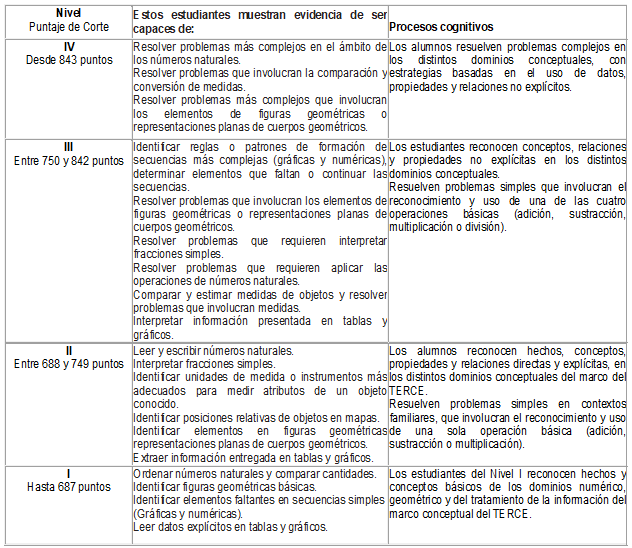
Fuente: Flotts et al., 2016, p. 59.
En lo que atañe a esta investigación, sólo circunscribimos este escrutinio al TERCE y específicamente se toma como objetivo general el analizar la evaluación del área de Matemáticas para 3º grado correspondiente a Paraguay en cuanto a niveles de performance que han alcanzado los escolares paraguayos y la relación entre estos y la Capacitación Continua de los maestros.
METODOLOGÍA
Para encontrar una respuesta al planteo de la investigación se procedió a construir nuevas tablas a partir de dos bases de Datos del TERCE en el formato SPSS, una correspondiente a los alumnos (PM3_all_TERCE.sav, Logros de Aprendizaje), otra a los docentes (QP3M.sav; Factores asociados), las tablas creadas se tabularon atendiendo a las variables: Identificador de clase (IDSCHOOL); ID del profesor (IDTEALIN); nivel (nivel de desempeño de los alumnos del 3º grado); las variables DQPIT12_01 (¿Ha participado en alguna de las siguientes actividades..._He realizado un magíster?); DQPIT12_02 (¿Ha participado en alguna de las siguientes actividades..._He realizado un diplomado?); y DQPIT12_04 (¿Ha participado en alguna de las siguientes actividades..._He realizado un curso de perfeccionamiento en matemática?)
Se procedió a crear una tabla de contingencia integrada, en la cual se identificaron todos los docentes con Magister, Diplomado o Especialización en Matemáticas. Así otra tabla en la cual se identificaban los maestros sin ninguna capacitación continua. Obtenidas estas tablas se construyeron tablas de contingencia en donde se cruzaron las variables docentes con capacitación continua (Magister, Diplomado o Especialización en Matemáticas) y cantidad de alumnos por niveles de desempeño, de este modo se pudo conocer los resultados de cada docente en cuanto al performance de sus alumnos de clase. Se construyó otra tabla de contingencia con los docentes sin capacitación continua y la performance de sus alumnos de clase. Con ambas tablas a la vista se procedió a la tabulación en cuanto extraer la cantidad exacta de alumnos de clase y los niveles alcanzados por estos.
RESULTADOS Y DISCUSIÓN
La distribución de docentes en la muestra del TERCE según se haya capacitado (D-CC) o no (D-sin CC) fue de 95 (45%) para D-CC y 116 (55%) para D sin CC. Es así que tenemos un total de 211 maestros evaluados en el TERCE para el caso Paraguay. De esta muestra el 45% es docente con capacitación continua y el 55% docente sin capacitación continua.
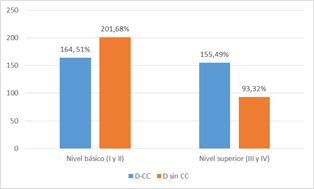
Para el caso de los maestros con capacitación continua y sin capacitación continúan, lograron el mismo porcentaje (25%) de sus alumnos alcancen el nivel IV. Para el nivel III, los maestros con capacitación continua lograron que el 63% de sus alumnos alcancen el nivel III en las pruebas TERCE de Matemáticas, mientras que los maestros sin capacitación continua lograron el 55%. En cuanto a los alumnos que se encuentran en la franja del nivel II, los maestros con capacitación continua los tienen en un orden del 76%, y los maestros sin capacitación continua en un 82%. En lo que refiere al nivel I, los maestros con capacitación continua tienen un 97% de alumnos en el nivel, mientras que los maestros sin capacitación continua tienen un 91% de alumnos en la franja (Gráfico 1).
La distribución agrupada según niveles, se encontró en el nivel básico (I y II) 51% para docentes con capacitación y en el nivel superior (III y IV) 49% de los docentes con capacitación continua cuyos alumnos han alcanzado los niveles superiores III y IV (Gráfico 2).
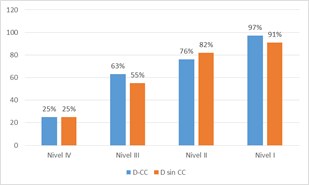
Gráfico 1 Docentes con capacitación y sin capacitación, cuyos alumnos han alcanzado niveles en las pruebas TERCE de Matemáticas.
Las capacitaciones son un medio para reflexionar sobre la formación profesional. Permite tomar decisiones y posibilita la oportunidad de compartir e intercambiar experiencias.
En la actualidad es indispensable incluir la formación matemática dentro de las competencias básicas que toda persona debe adquirir para enfrentar los desafíos de la vida y para ello los docentes que son encargados de la enseñanza formal de los estudiantes deben estar bien capacitados y los datos nos demuestran que si influye en los educandos que los docentes se encuentren capacitados.
En el estudio realizado por Ma, L (1999) sobre maestros de primaria del área de matemáticas de Estados Unidos y China, la autora concluye que los profesores chinos tienen un fondo de conocimientos muy rico de las matemáticas elementales en el plano conceptual tanto en el relacional de unos constructos con otros hasta alcanzar grados mayores de complejidad. A la par estos maestros son muy hábiles en cuanto a competencias propias en el campo didáctico para representar y explicar los tópicos de estudio. Estos docentes expertos en matemáticas integran armónicamente por un lado el contenido matemático y por el otro el contenido didáctico de aquellos.
Según la OEI (2009) desde la mitad del siglo XX a la actualidad hubo cambios trascendentales en lo que se considera el conocimiento profesional de un docente de matemáticas, proponiéndose una mirada que integra el conocimiento disciplinar y el didáctico.
Uno de los momentos importantes para el estudio del conocimiento profesional del profesor fueron los trabajos de Shulman de 1986 y 1987, que buscaban resaltar la importancia del conocimiento del contenido para la enseñanza y diferenciarlo del conocimiento del contenido que tienen otros profesionales. Estos trabajos centraron su atención en el profesor desde una perspectiva del conocimiento del contenido para la enseñanza y materia a enseñar, intentando contrarrestar lo producido en los años 80, donde el interés se enfocaba en los aspectos generales de la enseñanza, más que en el conocimiento del profesor como enseñante de un contenido (Rojas González, 2014, p. 44).
Como se expresa en el informe de OCDE (2005) “Contar con buenos docentes es garantía de buenas experiencias de aprendizaje”. En este estudio, se puede constatar en el gráfico 2, que los maestros con Capacitación Continua han logrado mayor eficacia en la enseñanza, pues se puede inferir esto del mayor porcentaje de alumnos que han alcanzado los niveles superiores III y IV en comparación con los docentes sin Capacitación Continua, de esta manera queda demostrada la correlación que existe entre la variable Capacitación Continua y la eficacia en la enseñanza para el caso de Paraguay en el informe TERCE.
CONCLUSIÓN
Un docente experto en matemáticas tiene muy bien definido su horizonte de objetivos, un universo rico de contenidos para enseñar con la debida pedagogía que le allana el camino por la senda más simple y efectiva para presentar materiales de clase del modo más simple y claro, es capaz de dirigir interesantes debates y conversaciones sobre temas complejos fluidamente, todo esto estimulando la participación, tomando las propias ideas de sus estudiantes y a partir de ahí redirigirlas hacia la meta cognitiva concreta. El docente capacitado busca resaltar la importancia del conocimiento del contenido para la enseñanza y diferenciarlo del conocimiento del contenido que tienen otros profesionales.