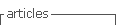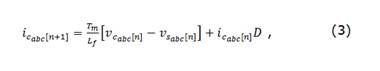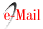INTRODUCCIÓN
Debido al crecimiento exponencial en el desarrollo energético económico, lo cual se ve reflejado en el rápido crecimiento industrial y en consecuencia la ampliación de las redes de distribución existentes, se requiere de un suministro fiable de energía y con elevados parámetros de calidad fundamentales para acompañar el crecimiento industrial; debido a que cualquier interrupción en el servicio o la mala calidad de la energía ocasionan importantes problemas técnicos y de producción, generando grandes pérdidas económicas a las industrias(Bose, 2010). Para mantener una elevada calidad de la energía en los sistemas eléctricos existen factores que requieren una mayor atención como ser el desequilibrio de carga, la presencia de corriente en el conductor neutro, el nivel de armónicos y la presencia de potencia reactiva, para solucionar los dos últimos inconvenientes se podrían utilizar filtros pasivos, existiendo una gama amplia de los mismos disponibles en el mercado, sin embargo no presentan una versatilidad para adecuarse a las variaciones propias de las cargas conectadas al sistema eléctrico, mientras que un filtro activo posee un comportamiento dinámico logrando adaptarse a las variaciones existentes en el sistema, logrando paliar los efectos adversos como el desequilibrio de carga y la presencia de corriente en el conductor neutro, motivo por el cual fue seleccionado para el presente trabajo como una solución viable y eficiente(Maciel, Morales, Gaona, & Pimentel, 2018). El filtro activo diseñado permite mejorar la calidad de la energía, aumentando los índices de fiabilidad y la estabilidad de la red eléctrica (Hu & He, 2008).
Los dispositivos tradicionales empleados en la electrónica de potencia como los convertidores basados en diodos y tiristores traen consigo problemas complejos debido a las no linealidades, que producen efectos no deseados, como ser un aumento en el índice de distorsión armónica total de corriente o voltaje, lo que provoca un aumento de las pérdidas en las líneas de transmisión y en los transformadores (Marzouki, et al., 2015). Debido al incremento de cargas tanto lineales como no lineales en las industrias y en los sistemas de distribución, el proceso de compensación de la energía reactiva y de los niveles de armónicos se vuelven cada vez más imprescindibles, motivo por el cual su reducción requiere una especial atención y para lo cual se plantea como alternativas el uso de filtros pasivos y filtros activos. El filtro pasivo presenta la desventaja de no ser una solución adaptativa a los cambios en la carga y es sensible a los efectos de resonancia con la red eléctrica, mientras que el filtro activo de potencia no depende de la impedancia de la red, pudiendo lograr una compensación dinámica de energía reactiva y niveles de armónicos, adaptándose además a los cambios en el sistema (Xu et al., 2005). Los filtros de potencia activa (APF), utilizados para reducción de los niveles de armónicos, así como de compensación de la energía reactiva presentes en la red, permiten mejorar la calidad de la energía, aumentando los índices de fiabilidad y la estabilidad de la red eléctrica (Marzouki, et al., 2015).
En un caso ideal, para reducir los componentes de energía oscilante que fluyen entre la fuente y las cargas, el voltaje y la corriente deben ser sinusoidales, en fase y equilibrados, para que así de este modo el sistema eléctrico pueda ser operado con mayor eficiencia y mejor calidad de la energía sin potencia reactiva, sin problemas de desequilibrio en la red de energía y sin presencia de corriente en el neutro; sin embargo, en casos prácticos, debido a las cargas comunes que son normalmente inductivo además de que existen cargas impredecibles en diferentes fases en un sistema trifásico, habrá energía reactiva que oscilaría en el sistema, existirían formas de onda de corriente desequilibrada distorsionadas(Lam et al., 2013). Para paliar estos problemas mencionados se introduce el principio básico de los compensadores paralelos, en este trabajo se plantea la utilización de un Filtro Activo de Potencia en paralelo con la carga de tal modo a que lo mencionado no afecte a la red del sistema eléctrico(Benslimane, Aloiuane, & Chetate, 2006).
Para la implementación del APF se debe seleccionar una estrategia de control adecuada, siendo empleado en el presente trabajo el control MPC. Una de las características más atractivas del MPC es su construcción abierta, que permite la incorporación de distintos tipos de modelos de predicción rápidamente, sean estos modelos lineales o no, ya sea de una variable o múltiples variables, así como la consideración de restricciones aplicables sobre las señales del sistema. El MPC ofrece la posibilidad de predecir futuras respuestas con base a un modelo de predicción y seguimiento de las referencias, así como la implementación de una función de coste y de este modo calcular las variables futuras para lograr que dentro del horizonte de predicción del MPC las variables controladas converjan en sus respectivos valores de referencia (Gregor, et al., 2016).
La actuación del MPC se basa en las activaciones de interruptores electrónicos de algún tipo de convertidor de potencia que determinan los niveles de tensión con el cual se optimiza la función de coste. Para este trabajo se escogieron dos convertidores de manera a realizar un análisis comparativo sobre la gama de ventajas y desventajas que presentan los mismos, los convertidores seleccionados son el convertidor de dos niveles en puente-H y el convertidor de siete niveles en cascada.
MATERIALES Y MÉTODOS
El tipo de investigación realizada es la descriptiva, que corresponde a una ciencia fáctica ya que el mismo se centra en la tecnología, y dentro de la cual se ha utilizado el diseño cuantitativo, teniendo en cuenta que fueron utilizadas las mediciones numéricas de manera a controlar los parámetros del Filtro Activo de Potencia por medio del control predictivo de corriente para lograr los objetivos propuestos de equilibrio de carga, la disminución de la potencia reactiva y la eliminación de la corriente del conductor neutro.
La población serían los convertidores empleados para el Filtro Activo de Potencia, mientras que la muestra corresponden los convertidores del tipo puente H empleados en dos topologías, la primera que otorga dos niveles de tensión a la salida y la segunda en una configuración en cascada que permite obtener siete niveles de tensión a la salida.
El trabajo fue validado por medio de simulaciones, utilizando el entorno de simulación Matlab/Simulink, en donde los circuitos a ser estudiados fueron montados de manera a verificar que las mediciones obtenidas mediante dichas simulaciones proporcionen los valores esperados según el modelo teórico. Para las simulaciones se tomaron valores obtenidos de manera heurística para lo que corresponde al filtro pasivo colocado en serie con el Filtro Activo de Potencia, mientras que los valores de carga no deberían ser significativos ya que al ser un filtro dinámico, éste debe ser capaz de adaptarse a las variaciones de la carga, siempre que ésta carga sea inferior a los niveles de potencia suministrado por el DClink, en el caso del convertidor de dos niveles se recomienda que suministre valores menores a 10MW y en el caso del convertidor de siete niveles para valores superiores a estos 10MW ya que son los valores que los mismos pueden proporcionar según las limitaciones de construcción.
Se realizaron mediciones de THD por medio del bloque TFF del Simulink, vistos desde el punto de vista del suministro eléctrico de manera a conocer el nivel de la distorsión armónica total introducido por el convertidor debido a las conmutaciones de los interruptores de potencia utilizados en cada fase y por el conductor neutro tras la conexión del Filtro Activo de Potencia a la red eléctrica. Se implementan voltímetrosa la salida del convertidor para verificar mediante mediciones de diferencia de potencial que el convertidor otorgue la cantidad de niveles de tensión esperados. En el lado de la carga y en el suministro de energía se requieren del uso de amperímetros para la medición de corrientes de carga y de red, junto con las mediciones de voltaje mencionadas, para el cálculo de las transformadas de Clark y Park utilizados para determinar los niveles de potencia activa y reactiva existentes.
A la salida del convertidor de potencia se requiere del uso de amperímetros para realizar las mediciones de corriente inyectadas por el Filtro Activo de Potencia, y de esa manera realizar y evaluar el seguimiento de corriente por parte del control predictivo. Por otro lado, a la salida del suministro de energía se requiere también del uso de amperímetros para visualizar el equilibrio de corriente. Para verificar la eliminación de la corriente por el conductor neutro se requiere de la medición de dicho parámetro. Finalmente, se implementa el uso de un vatímetro visto desde el punto de vista de la red para apreciar la compensación de la potencia reactiva.
HIPÓTESIS
El empleo de convertidores en puente H aplicados al diseño de Filtros Activos de Potencia pueden compensar la potencia reactiva, eliminar la corriente en el neutro y equilibrar la corriente en las fases.
PREGUNTAS DE LA INVESTIGACIÓN
¿Es posible obtener la corriente necesaria a partir de los niveles disponibles para generar una corriente que logre compensar la potencia reactiva?
¿Es posible obtener la corriente necesaria a partir de los niveles disponibles para generar una corriente que logre eliminar la corriente en el neutro?
¿Es posible equilibrar las corrientes de fase del sistema a partir de un filtro activo de potencia?
RESULTADOS
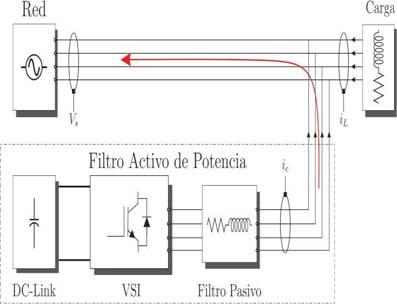
Las ecuaciones matemáticas que modelan el comportamiento del sistema se obtienen mediante el análisis del circuito equivalente del mismo. Del análisis de las leyes de Kirchhoff se obtiene la ecuación (1) y (2), por medio de las cuales es posible controlar las variables prediciendo el valor de las mismas, estas ecuaciones son discretizadas por el método de Euler hacia delante, resultando en la ecuación (3) y finalmente es posible obtener la ecuación de predicción, siendo ésta la ecuación (4). En sistemas de primer orden es un requerimiento conocer cuáles son las variables que son posible medir para el modelo predictivo y en el caso de que no puedan ser medidas calcular la estimación de estas. En la Figura 1 se observa el esquema del APF del cual se extraerán las ecuaciones que modelan la fase a, fases b y fase c.
Basándonos en la ley de Kirchhoff
Analizando una de las fases
entonces,
Discretizando tenemos:
Analizando el neutron
donde:
Se aplica el mismo procedimiento para obtener la corriente de referencia del neutro, por medio de la utilización de la ley de Kirchhoff recorriendo la malla del conductor neutro.
El control aplicado es el MPC, como se mencionó anteriormente, cuya característica es la de predecir las salidas futuras a través de estas ecuaciones previamente mencionadas, en este caso las predicciones realizadas son de las corrientes de salida del APF. Dicho control funciona prediciendo un nivel de voltaje para una VSI basado en el comportamiento de la corriente de referencia, la corriente de suministro medida y el voltaje de suministro, lo que hace que la corriente de salida pueda alcanzar el objetivo de referencia deseado al final del período de muestreo, para ello es necesario respaldarse en las transformadas de Clarke de potencia invariante para la generación de la referencia, ésta transformada consiste en el paso de un sistema de referencia de tres ejes coplanares a un sistema de tres ejes ortogonales (de abc a αβ0) (Lam et al., 2013) donde las corrientes de referencia se obtienen tras aplicar las transformadas inversas de las potencias de referencia p* y q*.
Inicialmente a las Corrientes medidas en la fase del Sistema se les aplica la transformada de Clarke vista en la ecuación (6) para obtenerlas en el Sistema ortogonal alpha beta cero y posteriormente pueda ser efectuada la transformada de Park vista en la ecuación (8 ) de donde se obtendrá las potencias activa, reactiva y cero del Sistema, la corriente de referencia del neutro será obtenida de la sumatoria entre corrientes de las fases del sistema, una vez que sean obtenidas las potencia activa y reactiva de referencia se procede a realizar la transformada inversa para tener las referencias en el sistema de tres ejes coplanares abc y esta pueda ser utilizada en el control predictivo en el cual emplearemos este sistema de tres ejes. La potencia activa total del sistema está conformada por la suma entre la potencia oscilante y la potencia promedio vista en la ecuación (9), como referencia tomamos el inverso aditivo de la potencia activa oscilante y como potencia reactiva de referencia el inverso aditivo de la potencia reactiva total del sistema.
El control predictivo fue escogido debido a que el mismo es bastante intuitivo y aplicable a prácticamente cualquier sistema cuyo modelo de sistema sea conocido, la calidad del control depende de la calidad del modelo, cuanto más preciso sea este, se tendrá un mejor seguimiento de corriente de referencia, una de las grandes ventajas que lo hacen más llamativo es la facilidad de inclusión de las no linealidades en las estrategias de control, para aplicarlo se recurre a una función de costo la cual es utilizada para realizar la selección correcta de la salida de tensión del convertidor, evaluando el mismo en los vectores de activaciones disponibles, para poder minimizar el cuadrado de la diferencia entre el valor calculado y el medido, este valor calculado emplea la ecuación extraída del modelado matemático.
Este trabajo se centra en la realización de la compensación de la energía reactiva, en el equilibrio de corriente de fase y en la reducción de la corriente del neutro por medio de un convertidor empleado como APF cuya función es la de inyectar corriente que logre paliar todos los puntos mencionados, esta inyección de corriente se realiza en el PCC y conectado en paralelo a la carga, se requiere el uso de un convertidor por línea y uno para el neutro además, estos convertidores son implementados en una configuración de dos niveles o en la configuración en cascada de manera a obtener un mayor número de niveles de tensión como se observa en la Figura 2 (a) y (b) respectivamente.
Figura 2: (a) Topología del APF de dos niveles en puente-H, (b) Topología del APF de siete niveles en cascada.
Se utilizaron simulaciones dentro del entorno Matlab/Simulink a modo de validar el trabajo, empleando los siguientes parámetros de simulación mostrados en la Tabla 1, utilizadas tanto para el convertidor de dos niveles como en el de siete niveles. Los parámetros de las cargas se observan en la Tabla 2.
Tabla 2: Parámetros de carga
| Carga desequilibrada | |||
| Fase a | Fase b | Fase c | |
| Resistencia (R) | 205 Ω | 112,5 Ω | 45 Ω |
| Inductancia (L) | 1,1 mH | 0,55 mH | 0,22 mH |
Para todos los casos se toma en cuenta que el filtro se encuentra inactivo hasta alcanzar los 0,02 s con el objetivo de que pueda visualizarse la incidencia del filtro activo de potencia. Para las primeras figuras se tiene el escenario de carga descrito en la Tabla 2 donde vemos los valores de la carga desequilibrada por fase, los parámetros de los transistores IGBT empleados como interruptor y un tiempo de muestreo de 0,04 ms.
Se estaría presentando primeramente los resultados correspondientes al convertidor de dos niveles alternando con la de siete niveles para apreciar las diferencias en las mismas.
En la Figura 3 se observa la medición de las potencias en el sistema, tras la activación del filtro activo, la potencia reactiva pasa de un valor inicial de 780 VAR a un valor aproximado de 100 VAR.
Se logra obtener los valores esperados en cuanto a potencia activa y reactiva en el convertidor de 7 niveles, al igual que en el convertidor de dos niveles, no obstante, según se observa en la Figura 4 se presenta una forma de onda con menos rizado en comparación a la Figura 3.
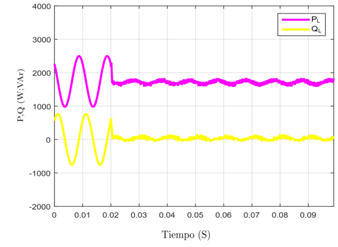
Figura 3: Potencia Activa y Reactiva en el sistema antes y después de la compensación realizada por el filtro correspondiente al convertidor de dos niveles.
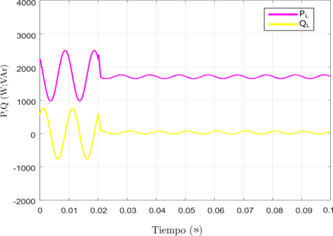
Figura 4: Potencia Activa y Reactiva en el sistema antes y después de la compensación realizada por el filtro correspondiente al convertidor de siete niveles.
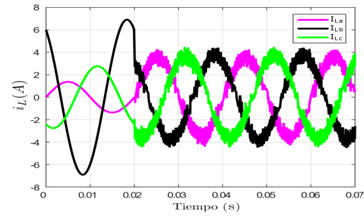
En la Figura 5 se observan las formas de onda de las corrientes que circulan en cada fase donde las mismas previamente a la conexión del filtro se encuentran en desequilibrio con una magnitud de ILa= 1,65∠0°A, ILb= 2,75∠-120°A y ILc= 7∠120°A, una vez que el filtro entra en funcionamiento se observa que las corrientes de fase quedan equilibradas, pasando así a los siguientes valores ILa= 3,6∠0°A, ILb= 4∠-120°A y ILc= 4∠120°A.
En la Figura 6 se observa una corriente en el neutro con un valor inicial de 5A antes de la conexión del APF a la red, y tras su conexión se logra reducir a un valor de prácticamente de 0,05 A amperios, lo cual se mantiene independientemente del cambio que pueda ocurrir en la carga, ya que se utiliza un control independiente para realizar la eliminación de la corriente en el neutro.
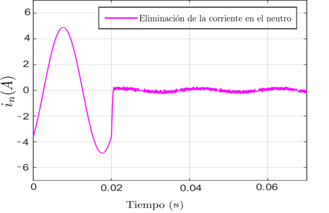
Figura 6: Forma de onda de la corriente del neutro antes y después de la activación del APF utilizando el convertidor de dos niveles.
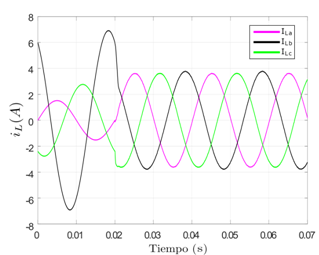
En la Figura 7 se aprecia que las corrientes de fase también se logran equilibrar con el empleo del convertidor de siete niveles, no obstante se presenta una senoidal limpia y sin rizado en cada fase con respecto a lo obtenido en el convertidor de dos niveles, lo cual es un factor relevante ya que el propósito siempre es suministrar buena calidad de energía, está mejor forma de onda en las fases se debe a que el convertidor de siete niveles cuenta con un mejor seguimiento de corriente de referencia debido a su mayor nivel de tensiones disponibles para generar las corrientes inyectadas por el filtro.
Con la inserción de un APF en el conductor neutro se busca aproximar esta corriente a cero, por lo que no influiría si la forma de onda presenta mayor o menor rizado, sino más bien la cercanía de la medición de la misma 0,2 A con el convertidor de siete niveles no se cuenta con rizado como se ve en la Figura 8, a diferencia del resultado obtenido con el de dos niveles que sí presenta un gran rizado como se aprecia en la Figura 6.
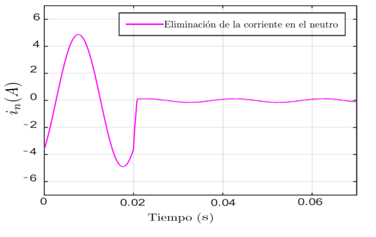
Figura 8: Forma de onda de la corriente del neutro antes y después de la activación del APF utilizando el convertidor de siete niveles.
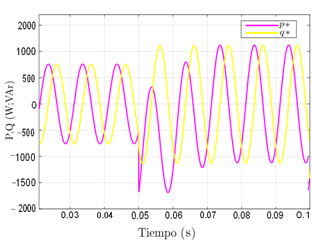
Se plantea un cambio en las potencias de referencia, este cambio se observa en la Figura 9, cuyo cambio de carga se encuentra en la Tabla 3, en cuanto a la potencia activa la misma ante un cambio de carga tarda en alcanzar su valor un tiempo de 0,02 s, esto se debe a que como la misma es obtenida tras de la diferencia entre la potencia filtrada y medida en el sistema se retrasa unos segundos su cálculo, este efecto queda presente en todas las gráficas.
En la Tabla 3 se observa el nuevo valor de las cargas de desequilibrio el cual se aplica a los 0,05 s.
Tabla 3: Parámetros de carga.
| Cargades equilibrada | |||
| Fase a | Fase b | Fase c | |
| Resistencia (R) | 230 Ω | 125 Ω | 55 Ω |
| Inductancia (L) | 1,01 mH | 0,505 mH | 0,202 mH |
Se aprecia en la Figura 10 que tras el cambio de carga, siendo este cambio aún desequilibrado, existe un cambio de corriente en las fases por lo que se debe tener una nueva referencia para la inyección de corriente en el filtro, en t = 0.07 s se logra nuevamente un equilibrio de entre corrientes de fase.

Figura 10: Equilibrio de carga en las fases luego del segundo cambio de carga en el convertidor de dos niveles
En la Figura 11 se aprecia que las corrientes de fase también se logran equilibrar con el empleo del convertidor de siete niveles, no obstante se presenta una senoide limpia y sin rizado en cada fase con respecto a lo obtenido en el convertidor de dos niveles, lo cual es un factor relevante ya que el propósito siempre es suministrar buena calidad de energía, está mejor forma de onda en las fases se debe a que el convertidor de siete niveles cuenta con un mejor seguimiento de corriente de referencia debido a su mayor nivel de tensiones disponibles para generar las corrientes inyectadas por el filtro.
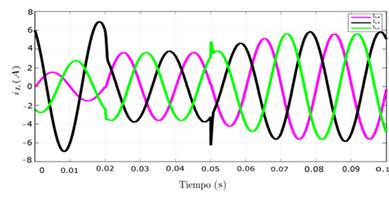
Figura 11: Equilibrio de carga en las fases luego del segundo cambio de carga en el convertidor de siete niveles.
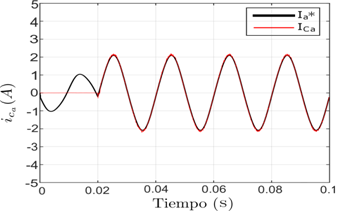
Ante este cambio en la carga, se alcanza el seguimiento de la nueva referencia en un tiempo de t = 2 ms, donde se expresa la corriente introducida por el filtro para cada fase adecuándose así el APF a la nueva situación presentada en el sistema, lo cual se aprecia en las Figuras 12 (a), (b), (c) y (d) en el caso del convertidor de dos niveles.
El convertidor de siete niveles también se logra adaptarse al cambio pero presentando un menor rizado, como se muestra en las Figuras 13 (a), (b), (c) y (d).
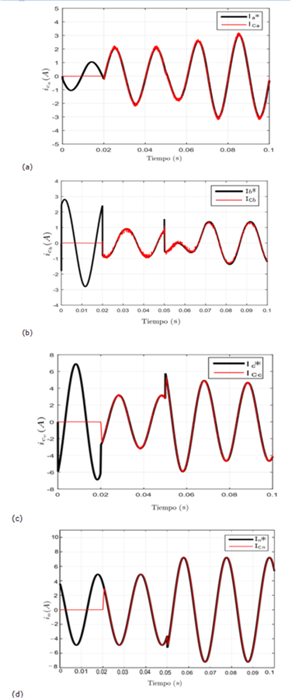
Figura 12: Seguimiento de la corriente de referencia del filtro en el convertidor de dos niveles de: (a) la fase a, (b) la fase b, (c) la fase c y (d) Seguimiento de la corriente de referencia del filtro del neutro.
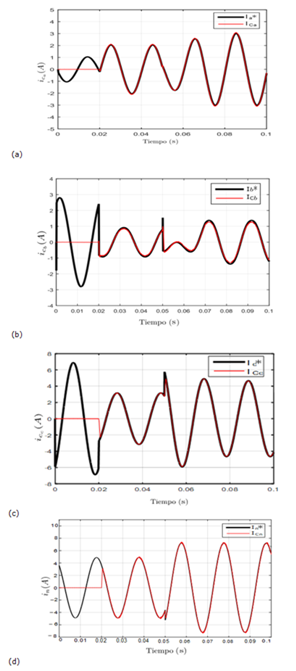
Figura 13: Seguimiento de la corriente de referencia del filtro en el convertidor de siete niveles de: (a) la fase a, (b) la fase b, (c) la fase c y (d) Seguimiento de la corriente de referencia del filtro del neutro.
Se realizó un análisis de sensibilidad donde se empleó en la simulación un Tm de 10 µs y un Tm de 100 µs.
Si bien en ambos casos se presenta un buen seguimiento como se aprecia en las Figura 14 y Figura 15, que en el caso de Tm igual a 10 µs existe un mayor rizado.
También se ha realizado un análisis de la Transformada rápida de Fourier (FFT) para evaluar la distorsión armónica de corriente (THD) para el convertidor de dos niveles y para el de siete niveles, donde primeramente se presentarán los resultados obtenidos de la fase a, b y c respectivamente en el convertidor de dos niveles Figura 16 (a), (b) y (c) donde los mismos son presentados por fase vistos en la Figura 16 desde el punto de vista del suministro de la red con un valor de 2,46%, 2,49%, 2.41% en las fases a, b y c respectivamente.
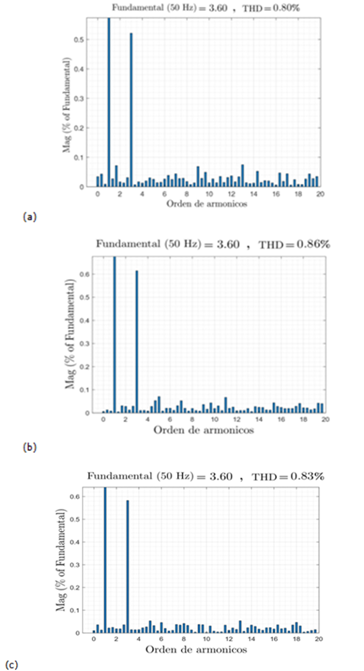
Mientras que en el convertidor de siete niveles un valor de 0.8%, 0.86%, 0.83% respectivamente en las fases a, b y c, como se indica en la Figura 17 (a), (b) y (c).
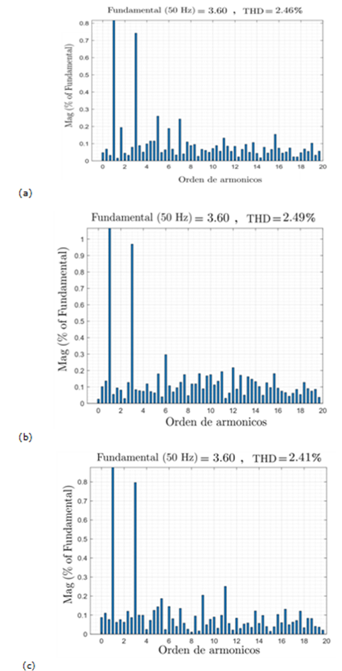
Figura 16: Distorsión armónica vista desde el suministro de energía de la: (a) Fase a, (b) Fase b y (c) Fase c; utilizando el convertidor de dos niveles.
DISCUSIÓN
Se obtuvo un buen seguimiento del control propuesto para el APF, puesto que se logró la compensación de la potencia reactiva, el equilibrio de carga y la eliminación de la corriente en el neutro en el sistema por ambos casos. En un caso de mayor requerimiento por las cargas el mismo logrará adecuarse a dicho requerimiento siempre que el APF logre obtener la corriente suficiente a partir de los niveles de tensiones disponibles, este nivel de tensión es dependiente de la potencia que pueda suministrar el DC link, lo cual dependerá del nivel de tensión que puede ser obtenido a través del convertidor.
Resaltando el costo computacional se tienen valores de tiempo con una razón entre el tiempo de ejecución del convertidor de dos niveles y el de siete niveles a casi 2.21 en cuanto al tiempo de ejecución, lo cual implica un costo computacional inferior en el caso del convertidor de dos niveles.
El sistema es sensible al filtro pasivo que se encuentra en serie con el APF, el mismo afecta en su funcionalidad ya que repercute directamente en la ecuación del modelado matemático en la cual se aprecia que estos parámetros se encuentran presentes.
La estructura del convertidor multinivel permite un mantenimiento más sencillo y la redundancia que proporcionan los niveles de tensión permite aumentar el grado de fiabilidad del sistema y su flexibilidad ante una demanda superior del sistema permite abastecer y adaptarse al mismo sin necesidad de componentes adicionales, simplemente utilizando fuentes de tensiones diferentes
Se propone como futura investigación la validación del trabajo por medio de resultados experimentales ya que los mismos solo fueron validados de manera teórica por medio del simulador Matlab/Simulink, y a su vez la expansión del trabajo hacia horizontes de corrección de armónicos.