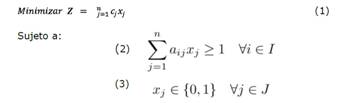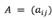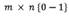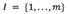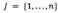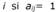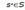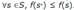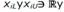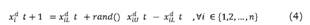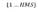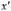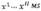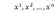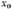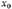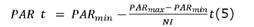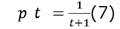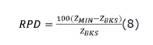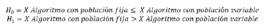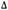INTRODUCCIÓN
Las metaheurísticas (MH) son algoritmos de optimización muy utilizados en las ciencias de la computación y matemáticas aplicadas. Las MH se aplican a problemas de optimización que no tienen algoritmo o heurística específica que dé una solución satisfactoria; o bien cuando no es posible implementar una técnica completa dado su alto costo computacional. Este tipo de algoritmos pertenece a la Inteligencia Artificial (IA). Las MH generan interés en diversas tecnologías, industrias y servicios dada su eficiencia en resolver problemas de optimización de diferentes dominios (Torres-Jiménez & Pavón, 2014). La parametrización de la MH es crucial para resolver las instancias del Set Covering Problem (SCP) (Birattari et al., 2002). Dentro de los parámetros que recibe la MH, se encuentra el tamaño de la población de soluciones o cantidad de soluciones en memoria. La división de población de soluciones fue tratada en (Turky & Abdullah, 2014), con buenos resultados. La versión propuesta por Turky y Abdullah no trabaja con SCP. En el presente trabajo, se identificó el efecto positivo de aumentar la cantidad de soluciones en el espacio de memoria durante la ejecución del algoritmo, mediante un nuevo operador de HS. Se comparó el comportamiento de la MH utilizando Población de soluciones Fijas (PF) contra Población de soluciones Variables (PV). Ambos métodos fueron probados contra las instancias de la librería o benchmark OR (Beasley, 1990). La meta de este trabajo consistió en determinar la mejor estrategia para solucionar el SCP ya sea usando PF o PV. El trabajo se estructura de la siguiente manera: En la sección Introducción se realiza una descripción de alto nivel de la técnica de inteligencia artificial usada y se presenta brevemente la estructura de trabajo que proporcionó los resultados que permiten hacer comparativas y conclusiones. Posteriormente en la sección Materiales y Métodos se aborda la MH Harmony Search (HS) original, pasando por una pequeña muestra de algunas variaciones presentes en otros estudios, adicionalmente se propone una nueva variación de HS con la cual se resolverá el SCP. De igual modo se describe formalmente en términos matemáticos el problema a resolver. En la sección Resultados se despliegan los valores obtenidos por la MH, los cuales son analizados en profundidad para pasar a la sección Discusión y Conclusiones.
MATERIALES Y MÉTODOS
El SCP es un problema matemático, el cual intenta cubrir un conjunto de necesidades al menor costo posible (minimización). El SCP fue incluido en la lista de 21 problemas NP-completos de Karp (Karp, 2010). Existen muchos usos prácticos para este problema como son: Localización de unidades de conexión en redes vehiculares (Sarubbi et al., 2017), ubicación de instalaciones (Crawford et al., 2017), ruteo de vehículos (Cacchiani, Hemmelmayr, & Tricoire, 2014; Prata, 2016; Yakici, 2017), asignación de tráfico en sistemas de comunicación satelitales (Ribeiro, Minoux, & Penna, 1989; Ceria, Nobili, & Sassano, 1998), asignación de tripulantes en líneas aéreas (Housos & Elmroth, 1997), asignación y ruteo de trenes (Samà et al., 2015), control de acceso basado en roles (Chen & Crampton, 2009) entre otros.
El SCP puede ser formulado como sigue:
Sea
una matriz donde y son las filas y columnas respectivamente. Formalmente podemos decir que la columna j puede cubrir a la fila . El vector Cj contiene valores no negativos que representan el costo de seleccionar la columna j y xj es la variable de decisión, la cual puede tomar el valor 1 si la columna j es seleccionada o 0 si no.HS es un algoritmo metaheurístico del tipo poblacional (Beheshti & Shamsuddin, 2013)como son: Artificial Bee Colony (ABC) (Crawford et al., 2014), Black Hole (BH) (Gómez et al., 2016) y Soccer League Competition (SLC)(Jaramillo et al., 2016). HS está inspirada en el proceso de búsqueda de un estado de armonía perfecto o Aesthetic Quality of Harmony (AQH) en la improvisación musical. Fue propuesto por (Geem, Kim, & Loganathan, 2001). La idea de esta MH es mimetizar el proceso realizado por músicos cuando improvisan. Las armonías que pueden ser generadas, dependen directamente del tono o rango de frecuencia del instrumento (Geem, 2009). En el proceso de improvisación musical, todos los músicos ejecutan acordes en un posible rango al mismo tiempo, para generar una armonía. Si todos los acordes generan una buena armonía, cada músico almacena en su memoria esa experiencia y posibilita la ejecución de una buena armonía en la siguiente improvisación. Lo mismo en la optimización: La solución inicial es generada aleatoriamente con las variables de decisión en el rango predefinido. Si al evaluar la solución en la función objetivo, se obtiene un buen valor, quiere decir que hay una buena oportunidad de mejorar en la próxima iteración. La función objetivo permite definir una relación de orden total entre cualquier par de soluciones del espacio de búsqueda. El óptimo global en minimización, es definido como una solución
, donde S corresponde al conjunto total de soluciones. s* posee el mejor fitness (menor valor) al ser evaluada en la función objetivo que cualquier otra solución del espacio de búsqueda, i.e., . El fitness corresponde al valor obtenido al evaluar la solución en la función objetivo.La MH HS, consta de 5 pasos en su versión original (Zou et al., 2011).
Dichos pasos serán revisados en detalle a continuación:
Paso 1: Inicialización del problema y los parámetros del algoritmo. Los parámetros
y corresponden a los valores inferiores y superiores de losdominios de las variables de decisión. Los parámetros requeridos para solucionar el problema de optimización son los siguientes: Harmony Memory (HM), el cual es un espacio de memoria donde se almacenan las armonías; Harmony Memory Size (HMS) que corresponde al número de vectores de soluciones en HM; Harmony Memory Consideration Rate (HMCR) el cual determina el ratio de selección de valores desde memoria; Pitch Adjusting Rate (PAR) la cual determina la probabilidad de mejoras locales y finalmente el número de improvisaciones (NI).
Paso 2: Inicialización del espacio de memoria HM hasta completar el HMS. Las armonías se improvisan de acuerdo a la ecuación(4).
donde:
t= Iteración o improvisación actual.
d= i-ésima variable del vector solución o armonía.
i= i-ésima solución o armonía
xdi(t + 1) = Representa a la siguiente solución.
xdiL(t) = Valor inferior de la variable de decisión, dado d y i.
xdiU(t) = Valor superior de la variable de decisión, dado d y i.
rand() = Corresponde a un valor aleatorio de una distribución uniforme dentro del rango
(0,1)
Paso 3: La improvisación de una nueva armonía
se especifica en Algoritmo 1. De acuerdo al proceso, se generan vectores del tipo .Estos vectores componen una matriz como la Figura 1.
Paso 4: Actualización de HM. Si la nueva armonía generada x´=
generada tiene mejor fitness que la peor armonía reemplaza la peor armonía en HM con la nueva armonía tal como se muestra en el Algoritmo 2; de lo contrario se continua con el paso siguiente.Paso 5: Si el criterio de detención (e.g. máximo número de Improvisaciones NI) se ha alcanzado, entonces la ejecución del algoritmo finaliza. Por el contrario, se continua la ejecución a partir del paso 3.
Con el propósito de mejorar el desempeño en la cobertura de HS tradicional y mejorar ciertas deficiencias de esta MH, se presenta Global-Best Harmony Search (GHS), desarrollada por (Omran & Mahdavi, 2008). La característica de esta variación de HS, es la generación de la población inicial aleatoriamente usando un Proceso de Bernoulli (Bertsekas & Tsitsiklis, 2002). Adicionalmente, se genera un vector solución
de manera elitista, basado en la idea de una relación de ganancia (profitratio), donde se verifica si x es mejor que xworst en HM entonces xworst es reemplazado por . La metaheurística GHS ajusta dinámicamente el parámetro PAR de acuerdo a la ecuación (5):
HS tradicional es buena explorando el espacio de búsqueda, pero no lo es tanto a la hora de explotar (Xiang et al., 2014). No existe un equilibrio entre la exploración y la explotación. HS fue pensada para ser utilizada en un espacio de búsqueda continua y no puede ser aplicada para resolver problemas de optimización combinatoria discretos. Para mejorar estos y otros aspectos se propone la variación de HS denominada Binary Global-Best Harmony Search (BGBHS). BGBHS, hace uso de los siguientes operadores: PAR, HMCR, operador de reparación, mecanismo de selección elitista y ajuste dinámico del parámetro p de Bernoulli entre otros.
El parámetro HMCR con valores altos, acelerar la velocidad de convergencia, con valores bajos permite escapar de óptimos locales, lo cual puede ser de gran utilidad hacia el fin de la ejecución. Detalle en ecuación (6).
 donde: () = Harmony Memory Consideration Rate para la iteración . = Mínimo valor que puede tomar . = Máximo valor que puede tomar HMCR. = Número de improvisaciones o iteraciones. = Iteración o improvisación actual.
donde: () = Harmony Memory Consideration Rate para la iteración . = Mínimo valor que puede tomar . = Máximo valor que puede tomar HMCR. = Número de improvisaciones o iteraciones. = Iteración o improvisación actual.Con el fin de mejorar la exploración en BGBHS (Salas et al., 2016), se propone una variación dinámica del parámetro de probabilidad p de Bernoulli al generar la población inicial. El parámetro p parte con el valor 0,5 en la iteración o improvisación t = 1 y decrece con cada iteración, tendiendo a cero. El comportamiento del parámetro se ajusta a la ecuación (7):
Este procedimiento permite que las soluciones al inicio de la generación tengan una mayor cantidad de variables activadas, debido a la alta probabilidad de éxito en el ensayo de Bernoulli. A medida que las iteraciones transcurran, el valor de p disminuye, lo cual produce que las soluciones tengan menos variables activadas. HM, presentará un amplio espectro de soluciones desde el inicio, lo cual contribuye a una mejor exploración del espacio de búsqueda.
Todas las armonías deben ser reparadas, dado que el proceso de Bernoulli no asegura la factibilidad de las soluciones generadas. El operador de reparación consiste de dos fases: la primera llamada ADD, donde se procede a activar columnas del vector de manera tal que este se vuelva factible; la segunda se denomina DROP y se aplica para eliminar columnas redundantes sin que ello afecte la factibilidad de la armonía. El detalle de este operador puede ser revisado en el Algoritmo 3.
Se agrega un comportamiento elitista al funcionamiento de la MH,
tratando de mejorar en cada iteración la mejor solución
o bien mejorando lapeor solución
existente en HM. Un detalle de este comportamiento puede ser revisado en el Algoritmo 4.
La operación que permite agregar soluciones al HM logrando la implementación automática de PV, se basa en el proceso de generación inicial de armonías, tomando en cuenta un porcentaje de no mejora. Si transcurridas 100 iteraciones, se detecta estancamiento en óptimo local, se desencadena un proceso que se explica en algoritmo 5. Esta operación permite al algoritmo escapar de óptimos locales, alcanzando una mejor exploración del espacio de búsqueda.
Extendiendo la inspiración original de la MH, podríamos decir que el proceso mencionado anteriormente correspondería a realizar una improvisación paralela y la mejor armonía obtenida de ese proceso sería incluida en el repertorio de la improvisación principal. La población paralela creada es eliminada.
RESULTADOS
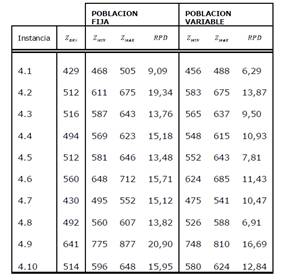
Con el fin de probar la correcta ejecución de la MH, se realizó 30 ejecuciones independientes de cada instancia del benchmark, tanto para HS PF como HS PV. El tiempo de ejecución de la MH contra cada uno del set de datos varió entre 2 y 120 minutos dependiendo del nivel de complejidad. La MH fue programada en lenguaje Python 2.7, haciendo uso de las librerías Numpy y Scipy. Como persistencia se utilizó archivos de texto y como procesamiento se contó con una máquina virtual con CPU doble núcleo 2.0 GHz (64 bit), 8GB de RAM, 80 GB de Disco Duro y sistema operativo Windows 7 Profesional de 64 bit. En las tablas expuestas en esta sección, la columna RPD reporta la desviación
porcentual relativa entre el menor valor obtenido experimentalmente Z y el óptimo global para esa instancia Z BKS (s∗). El RPD se calcula mediante la ecuación (8).
El △ RPD representa la diferencia entre el RPD de la PV y el RPD de la PF.
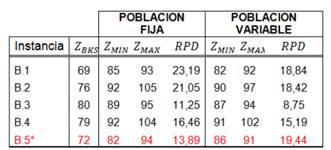
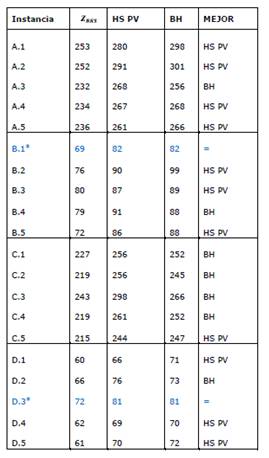
Tal como apreciamos, en la Tabla 1, los resultados obtenidos por PV para la instancia 4, fueron más cercanos al óptimo global, es decir: presentaron un mejor fitness. De todos los conjuntos de datos, con ambas técnicas no se llegó a obtener un óptimo global, sin embargo, los RPD se mantienen bajos.
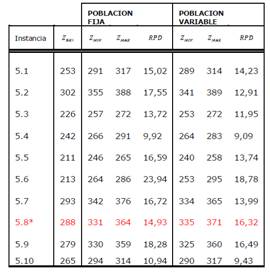
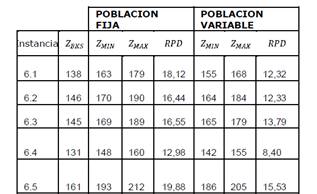
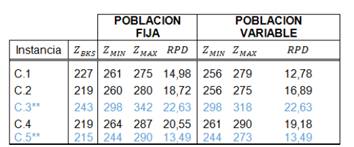
En la Tabla 2, se puede ver como la estrategia PV obtiene mejores los mejores resultados, excepto para el set 5.8*. Las Tablas 3 y 4 muestran como consistentemente la técnica con PV presentó mejor desempeño que la técnica con PF.
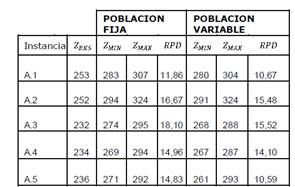
La Tabla 5, muestra que la técnica PF solo fue mejor en uno de los conjuntos de datos de la instancia B.5*.
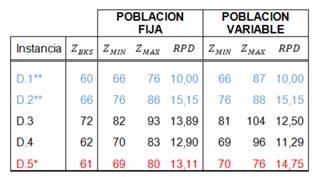
En las instancias superiores, C y D se presentan comportamientos donde ambas técnicas llegan a igualdad de soluciones, como es el caso de C.3**, C.5**, D.1** y D.2**. Solamente en la instancia D.5* la técnica con PF es mejor. Para el resto, PV obtiene resultados más cercanos al óptimo global.
En definitiva, PV obtuvo mejores o iguales resultados en 42 de los 45 set de datos, logrando una efectividad del 93.3%. Restando los empates, se presenta una ventaja de 84.4% para PV.
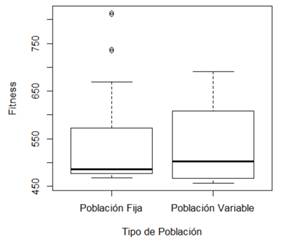
Con el fin de realizar un análisis estadístico de PF vs PF se deben eliminarlos outliers (observación estadística marcadamente diferente a otros valores de la muestra)de los resultados obtenidos. Una técnica de detección de outliers, puede ser mediante gráfica de cajas (Figura 2), donde se determina la existencia de ellos para los resultados del SCP41 con PF.
Luego de que se retiraron los outliers, se verificó la normalidad de los datos mediante los test Shapiro-Wilk (Shapiro&Wilk., 1965)y Kolmogorov-Smirnov-Lilliefors (Lilliefors, 1967), para lo cual se plantearon las siguientes hipótesis:
Dado los p-valores obtenidos en los test, se rechaza H0 . Estopermitióaplicar Wilcoxon-Mann-Whitney (Mann &Whitney, 1947).Para verificar superioridad de la estrategia de resolución con PV sobre PF, se define las hipótesis:
El programa estadístico R, obtuvo un p-valor < 0.05 por lo cual se
rechaza H0 y se acepta H esto implica que PV proporciona mejores resultados. Este procedimiento se extiende a cada instancia del Benchmark. Los resultados de este análisis son coincidentes con lo verificado mediante RPD.
Al comparar los resultados de instancias superiores de HS con PV contra BH (Gómez et al., 2016) nos damos cuenta que tanto en la instancia B.1* como D.3* ambos algoritmos llegan a los mismos resultados.
De las restantes 18 instancias, HS con PV obtiene mejores resultados en un total de 11 instancias. Esto representa un total de 61.1% (restando los empates) de eficacia en comparación con BH. Por grupo de instancias, el mejor desempeño para HS PV es la instancia A, el peor desempeño se presenta en la instancia C.
DISCUSIÓN Y CONCLUSIÓNES
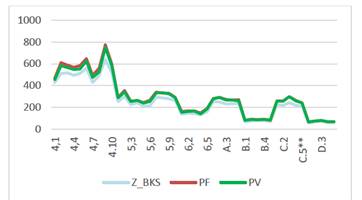
Los resultados comparados directamente a través de
RPD muestran que: en la mayoría de lasinstancias probadas, la versión de HS con PV es mejor. Los resultados obtenidos por instancias son representados en la Figura 3.
Consistentemente, el análisis estadístico realizado demuestra que el comportamiento de la MH con PV obtiene mejores o iguales resultados en 93.3% de las instancias vs PF. Llama la atención el hecho de que la variación de población encuentre mejores resultados incluso a menor cantidad de iteraciones lo cual es bastante prometedor debido a que disminuye el tiempo de procesamiento computacional, con lo cual muchos problemas pueden ser resueltos en una menor cantidad de tiempo.
En el presente trabajo se realizó una variación positiva en el tamaño de la población (Agregando soluciones al espacio en memoria hasta un máximo predefinido), pero no se profundizó en realizar un ajuste dinámico, en el sentido de agregar o quitar soluciones del espacio de memoria. Esto abre claramente la opción para investigar la posibilidad de utilizar una población completamente adaptativa o paralelas.
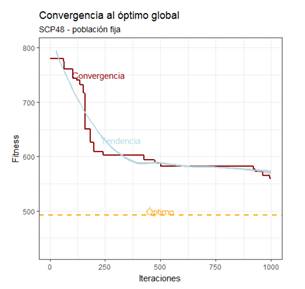
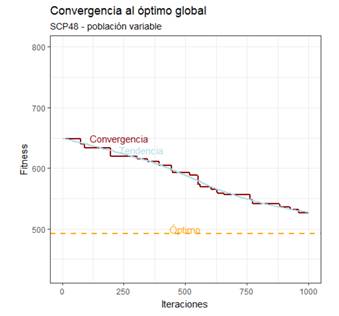
Si miramos la Figura 4, correspondiente al gráfico de convergencia muestra estancamiento en óptimos locales, claramente hacia el final la tendencia es asintótica a x. Por el contrario, la Figura 5 presenta un comportamiento siempre decreciente, sin estancamientos en óptimos locales, mostrando una gran capacidad de exploración, con tendencia al óptimo global.
Finalmente queda demostrado que para resolver problemas de optimización como SCP, es útil emplear PV en contraposición a PF. La comparativa contra BH muestra evidencia que HS con PV es mejor en el 61.1% de las instancias.