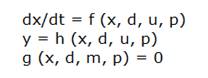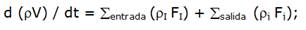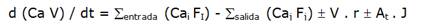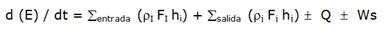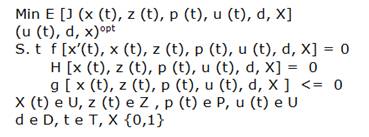Necesidad del respaldo experimental

El desarrollo de la industria de procesos químicos se ha fundamentado en el uso intensivo de métodos experimentarles, descansando en una concepción insigne de cómo percibir los fenómenos de transporte basado en las tradicionalmente utilizadas analogías entre las transferencias de impulso, de calor y de masa. (^{Ibarz y Barboza Cánovas; 2005})

No obstante, lo avanzado, los nuevos desarrollo industriales, utilizando diferentes tipos y calidades de materias primas, reclaman, sobre todo en las condiciones del reto de la asimilación y adecuación de las nuevas tecnología a las condiciones especificas de Cuba, que los centros de generación de conocimientos garanticen información en sus laboratorios que sirvan de respaldo a las decisiones inversionistas, no solo para tecnologías propias, sino también para las tecnologías foráneas que se nos propongan.

Una simple observación experimental en un laboratorio, en una instalación a escala piloto o a nivel industrial puede costar decenas o cientos de dólares. No obstante, lo anterior, el experimento ha sido siempre una gran herramienta en la solución de problemas prácticos y la verificación de hipótesis en la industria de procesos químicos. (Martínez Urreaga y otros; 2006)

Los métodos tradicionales de experimentación implican un considerable esfuerzo, tiempo y recursos para su ejecución elevando los costos de los resultados investigativos, sobre todo si son necesarios realizarlos a nivel de planta piloto o en escala industrial. Siendo el objetivo de la investigación obtener información sobre el fenómeno estudiado, para después actuar sobre el mismo, puede definirse la eficiencia de la investigación como la cantidad de información útil obtenida por unidad de costo, por consiguiente, es extremadamente importante para la investigación utilizar métodos experimentales que le brinden la máxima cantidad de información con el menor costo y esfuerzo. (^{Sampieri; 2010})

En la época actual, para acelerar los resultados y enfoques multilaterales de las investigaciones, los modernos métodos matemáticos se han convertido en un poderoso arsenal metodológico para la solución actuales y prospectivos y posibilitan ya, “no solo el desarrollo de los procesos óptimos, sino de problemas también la dirección de estos con vista a mantenerlos siempre en los regímenes óptimos y la ruta deseada (Kafarov; 1976).

El uso de los métodos de diseño de experimento

El uso del diseño estadístico de experimento facilita un incremento apreciable en la productividad de los investigadores, así como la confiabilidad de los resultados obtenidos, siendo estos métodos por su naturaleza universal aplicables en la mayoría de los campos de investigación y que significa una gran contribución a la optimización de la experimentación. No es necesaria una preparación especial en estadísticas o matemáticas para utilizar estos métodos, la experiencia ha demostrado que los ingenieros comprenden y aplican con éxito sus fundamentos. Por ello es idóneo incentivar a los estudiantes de Ingeniería Química a utilizar desde pregrados estos métodos de gran aplicación en la industria.

La idea de que un experimento se puede diseñar es de tiempos antiguos, sin embargo, sólo a principios del presente siglo, se introdujeron los métodos estadísticos de diseño de experimentos. En la década de los años cincuenta se inició una nueva etapa en los trabajos de Diseño de Experimentos encaminando los esfuerzos a encontrar las condiciones óptimas (^{Box y Wilson; 1951}).

El uso del Diseño de Experimento facilita un incremento apreciable de la productividad de los investigadores y de la confiabilidad de los resultados obtenidos, en general se puede afirmar que, si los experimentos se planifican inteligentemente, incorporando diseños estadísticos factoriales o diseños factoriales parciales (^{Box-Hunter; 1961}). La información obtenida es confiable y tiende a minimizar el número de experimentos necesarios; sin embargo, si el planteamiento de las experiencias se hace deficientemente, sin tener en cuenta los aspectos sofisticados del análisis, generalmente no se podrá reunir mucha información útil. Esto se debe a que de los experimentos planificados deficientemente no se obtienen la información principal.

En muchas investigaciones se plantean las interrogantes siguientes:

Se ha demostrado en la experiencia investigativa que experimentos desarrollados de forma simple pueden dar respuesta a ambas preguntas.

Los métodos de optimización permiten acentuar las diferencias de las épocas económicas, porque determinan la forma que se hacen las cosas en uno y otro nivel de desarrollo. Sin embargo, los métodos matemáticos de optimización por su propia naturaleza no pueden ser aplicados de forma directa a la realidad estudiada, sino a modelos matemáticos de determinado conjunto de manifestaciones del fenómeno estudiado, los que, al ser estudiados, solo presentan un nivel práctico si los mismos reflejan de un modo sufrientemente adecuado, las situaciones reales y satisfacen determinado grado de exactitud.

Según la complejidad de los sistemas se requerirá mayor o menor información, para obtenerla mayor o menor trabajo experimental. El esfuerzo de muchos investigadores durante los años de aplicación de estos métodos han contribuido a optimizar el trabajo experimental reduciendo los tiempos y esfuerzos para obtener resultados, siendo válido el análisis propuesto por ^{Isaccson (1970}).

La utilización de estos métodos formalizados permite por su estructuración el trabajo en equipos, incluyendo profesionales de reciente graduación y estudiantes, incluso en experimentos en condiciones industriales (^{Gonzalez Suarez y Miño Valdés; 2015}).

La modelación matemática fenomenológica, herramienta imprescindible para el Ing. Químico.

El modelo matemático de un proceso está definido como el conjunto de ecuaciones matemáticas que relacionan al conjunto de variables (magnitudes fisicoquímicas) y constantes (parámetros) que caracterizan el comportamiento del proceso. El comportamiento de un proceso permite su caracterización mediante los indicadores operacionales de producción, calidad, medioambientales, de seguridad tecnológica y económica. Los modelos matemáticos fenomenológicos son aquellos que se basan en leyes de la física (leyes de conservación) y los principios físicos químicos, cinéticos y termodinámicos, que rigen su comportamiento.

El modelo matemático que describe el comportamiento no estacionario del proceso, cuando las variables son dependientes del tiempo recibe el nombre de modelo dinámico del proceso. Este modelo es el más general y puede utilizarse para resolver cualesquiera de las tareas que le compete resolver a un Ingeniero Químico ya sea en el diseño, el análisis y operación y control de un proceso. De este puede deducirse el modelo de estado estacionario, cuando las variables permanecen invariantes con el tiempo, que es un caso particular idealizado del primero. Tradicionalmente el modelo de estado estacionario ha sido utilizado para resolver los problemas de diseño y de análisis, sin embargo el modelo dinámico es más general y permite por ello el logro de objetivos más integrales y exactos, tanto en procesos continuos como discontinuos. El modelo dinámico está basado en ecuaciones diferenciales que incluyen al tiempo como variable independiente. Las variables involucradas en dicho modelo son aquellas magnitudes químicas físicas que pueden cambiar durante la operación del proceso, debido a los efectos perturbadores de las etapas precedentes del proceso o a la influencia del entorno. Se incluyen siempre como variables operacionales aquellas que se identifican de manera más directa con los objetivos operacionales del proceso, que constituyen variables de salida, y además aquellas variables de entrada que contribuyen a perturbar el comportamiento operacional deseado, las cuales resultan ser las denominadas variables de disturbio. Por ello, los modelos dinámicos son un elemento útil para estudiar el comportamiento de un sistema tecnológico incluso en condiciones de variaciones en las variables de entrada al proceso y permite a los profesionales y estudiantes una completa comprensión de la tecnología en estudio. (^{Perry y Chilton; 1981})

También se incluyen como variables operacionales a todas las que se utilicen por el sistema de control del proceso para restablecer el comportamiento deseado del proceso, estas reciben el nombre de variables manipuladas.

Los modelos matemáticos de los procesos pueden ser formulados para diferentes escalas, hoy día a saber a escala nano, micro, meso y macro. Las primeras escalas, la nano y la micro, implican formulaciones complejas, basadas en la química y física molecular y en ecuaciones a derivadas parciales. El campo de trabajo de los Ingenieros químicos abarca hoy también estas escalas, pero en este trabajo abordaremos la escala macro exclusivamente. Los modelos dinámicos de los procesos a escala macro pueden plantearse generalmente mediante un sistema de ecuaciones diferenciales no lineales a derivadas totales, que tienen la forma:

Donde x(t) es el vector de variables de estado, d(t) y u(t) son los vectores de variables de disturbio y manipuladas respectivamente, p es el vector de parámetros e y(t) es el vector de las variables de salida.

Este sistema de ecuaciones se conoce en la literatura como Differential Algebraic Equation (DAE).

Confección del modelo matemático dinámico fenomenológico de un proceso.

Un modelo matemático de un proceso puede plantearse a partir de los balances de masa, energía y momentun. De estos resultan las denominadas ecuaciones de continuidad. Estas ecuaciones pueden plantearse considerando un macro-entorno o un micro-entorno y a partir de las leyes que definen el comportamiento fenomenológico del proceso, con una mayor o menor fidelidad o conocimiento del proceso. Hoy resultan muy utilizados los modelos que combinan ecuaciones empíricas con ecuaciones basadas en las leyes físicas químicas, a fin de sortear determinadas lagunas existentes en el conocimiento de los procesos o hacer más viable y sencilla la confección y/o solución del modelo en su totalidad. A los modelos basados en ecuaciones empíricas se les ha dado el nombre común de modelos de caja negra, pero cuando existe la combinación apuntada suele dárseles el nombre de modelos de caja gris o híbridos. Los modelos matemáticos de caja negra también pueden ser utilizados para describir el comportamiento dinámico de los procesos, pero hay que tener muy presente que la validez del modelo estará restringida por la región de experimentación y esto hace muy poco confiable su capacidad de predicción fuera de esta región.

Para confeccionar el modelo matemático de un proceso es necesario definir los siguientes aspectos:

El entorno de modelación, el cual se configura teniendo en cuenta el proceso que se desea modelar y sus partes.

La estructura o patrón de flujo del proceso. Generalmente se asume un patrón de flujo ideal de mezclado perfecto o de flujo pistón o combinación de estos. Para esto se tiene en cuenta el entorno de modelación y si el proceso puede suponerse de parámetros concentrados o de parámetros distribuidos, o mediante una combinación de modelos ideales, basados en estos patrones de flujo.

En los casos de patrones de flujo no ideales de procesos a parámetros distribuidos, cuando los gradientes no son despreciables y existen en diferentes direcciones espaciales, se opta por una solución intermedia discretizando el entorno de modelación mediante elementos o compartimentos finitos y considerando el elemento finito como un sistema a parámetros concentrados. De esta forma un proceso a parámetros distribuidos puede convertirse en un proceso equivalente aproximado de parámetros concentrados. El grado de aproximación depende del número de elementos o compartimentos considerados. Es decir, el mallado del entorno de modelación determina la complejidad del modelo matemático y de la solución del problema.

La cinética del proceso, dada por las etapas que controlan su velocidad. En este aspecto suelen utilizarse, muchas veces, ecuaciones empíricas, obtenidas por vía experimental y basadas en las leyes cinéticas conocidas para los procesos de reacción química, transferencia de masa, calor y momentun o en modelos estadísticos de regresión y/o redes neuronales.

Las ecuaciones de balance citadas. Si el proceso es de parámetros concentrados estas ecuaciones resultan sistemas de ecuaciones diferenciales a derivadas totales y la variable independiente siempre es el tiempo. Si es de parámetros distribuidos y se trata de describir por uno aproximado de parámetros concentrados el sistema de ecuaciones tiene las mismas características. En el caso de procesos de parámetros distribuidos el sistema de ecuaciones diferenciales resulta ser a derivadas parciales y las variables independientes serán el tiempo y las variables espaciales de que se trate. Se deben definir también las condiciones de frontera.

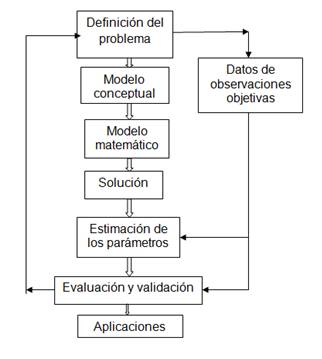
En la Figura 1 se pueden observar los pasos a dar para la confección de un modelo matemático.

La visión abarcadora y pormenorizada que exige un modelo dinámico es un factor clave para que los profesionales en los estudios de postgrado o los estudiantes de pregrado, profundicen en el conocimiento real de los procesos tecnológicos en estudio, haciendo hincapié en las aplicaciones de las leyes de semejanza de los fenómenos de transporte de impulso, calor y masa con una visión más completa que lo realizado con los métodos tradicionales por lo que son un elemento esencial en la formación de los profesionales de la Ingeniería Química.

Solución del modelo matemático dinámico

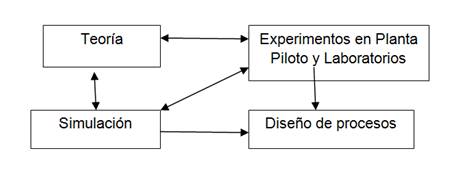
El nuevo paradigma del diseño de procesos para el siglo XXI, que se muestra en la figura siguiente, permite visualizar el enfoque holístico para la solución este problema en la Figura 2.

La solución del modelo matemático del proceso, una vez confeccionado, conlleva la verificación del ajuste de los parámetros desconocidos o inciertos del modelo y la validación del modelo en la región de experimentación y fuera de ella, a fin de conocer su potencialidad predictiva. Para ello hay que desarrollar experimentos que previamente deben ser diseñados cuidadosamente a fin de establecer la región de experimentación adecuada y las variables que deben ser consideradas en la experimentación.

La participación de estudiantes y profesionales en actividades de postgrado son de extremado interés ya que permiten la capacitación de los actores presentes y futuros de la comunidad científica de los diferentes sectores industriales en el uso de herramientas modernas de investigación que aceleran la generación y evaluación de la transferencia de conocimientos a la economía nacional.

Considerando que el patrón de flujo del proceso puede ser alterado con el cambio de escala, la experimentación debe realizarse en la escala más cercana posible al prototipo o debe tenerse muy presente este aspecto para aplicar el modelo matemático a una escala diferente. Para el ajuste de los parámetros del modelo frecuentemente se utiliza el método de la regresión no lineal múltiple.

La utilización de la computación en la solución de estos sistemas es obligada, a fin de obtener soluciones confiables y en el menor tiempo posible. El software profesional disponible para resolver sistemas de ecuaciones diferenciales hoy día es numeroso y permiten obtener los resultados con mínimo esfuerzo de programación e inversión de tiempo. Podemos mencionar como ejemplo el MATLAB, MATEMATICA, PSI, ASPEN-HYSYS, COMSOL, FLUEN, pero hay muchos otros.

Los problemas de mayor complejidad, con gradientes espaciales y geometrías no convencionales del entorno de modelación, que requieren de la solución de decenas de miles de ecuaciones implican la utilización de software para la solución de problemas de multifísica, o también denominados de CFD (Computational Fluid Dynamics), como el COMSOL y el FLUEN. Estos resuelven sistemas de ecuaciones diferenciales parciales, basados en balances de masa, calor y momentun, en entornos con geometría compleja.

Balances de Masa, de Energía y Momentun. Ecuaciones de Continuidad.

Los balances de masa, energía y de cantidad de movimiento se realizan considerando los términos de entrada, salida y acumulación de masa, energía y cantidad de movimiento respectivamente.

[Acumulación de la cantidad] / [tiempo] = [cantidad entrada] / [tiempo] - [cantidad salida] / [tiempo].

Donde cantidad puede ser: masa, energía o cantidad de movimiento.

Las expresiones generales resultantes son:

Balance total de masa:

V es el volumen (m³), ( es la densidad (kg/m³), F es el flujo (m³/h),

i para las corrientes de entrada; j para las salidas.

Balance de componente:

Ca es la concentración del componente (mol/m³), V es el volumen (m³), F es el flujo (m³/h), r es la transformación por reacción química [mol / (m³-h)], A_t es el área de transferencia (m²) y J es el flujo transferido [mol / (m²-h)].

Balance de energía:

E es la energía interna (U), mas la potencial (P), mas la cinética (k) en (kJ), h es la entalpía (kJ/kg),

Q es la energía transferida (kJ / h), Ws es el trabajo realizado por o entregado al proceso.

Este último es pocas veces utilizado en el caso de los balances de energía en los procesos. En la mayor parte de los casos prácticos el término de acumulación queda planteado en función de la energía interna, pues la potencial y la cinética pueden considerarse constantes, por lo cual para el caso de líquidos y sólidos puede utilizarse el término U = Cp.(.V.T y para gases Cv en vez de Cp.

T es la temperatura en ^oC, Cp es el calor específico a presión constante en kJ/(kg.^oC) y Cv es el calor específico a volumen constante.

El problema general de la Ingeniería química.

Una vez confeccionado el modelo este puede ser utilizado para la solución de cualquiera de los problemas particulares que debe resolver un Ing. Químico, ya sea el de diseño (o síntesis), el de análisis o el de control. Todos pueden ser resueltos integralmente, mediante el planteamiento del problema general de la Ing. Química, como un problema único, a partir de una formulación integral de este, como problema de optimización multiobjetivos de un sistema matemático de ecuaciones DAEM. Para su solución se utiliza la programación no lineal con enteros (MINLP).

Sistema DAEM, donde x: vector de variables de estado, z: algebraicas, p: parámetros Inciertos,

u: entradas manipuladas, d: diseño, X enteras. E es la esperanza matemática de la funcional múltiple J. u, d x son las variables a optimizar y el resto de las ecuaciones son las restricciones correspondiente de igualdad y desigualdad.

CONCLUSIONES