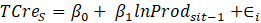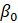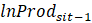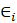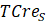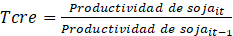INTRODUCCIÓN
La economía del Paraguay está fundamentada en la producción agropecuaria. El desempeño económico está directamente relacionada a la producción y a la exportación agropecuaria, específicamente soja, carne vacuna y cereales (Banco Mundial, 2014), que, al ser bienes primarios, presentan una dependencia de la variación de los precios internacionales, incrementando considerablemente la volatilidad del PIB y del desempeño económico del país. Otras dos características de la producción primaria del Paraguay son la dependencia de las condiciones climáticas, que según el Banco Mundial (2014) “las crisis relacionadas con el clima representan por sí solas más del 50% de la volatilidad del PIB agrícola del Paraguay”. La segunda se refiere a la dualidad de la agricultura paraguaya, en la cual se desarrollan agricultura empresarial conectada al agronegocio y una agricultura de subsistencia que siembra en pequeña escala (Torres & Lovois, 2009); (Ferreira & Vázquez, 2015), (Programa de las Naciones Unidas para el Desarrollo, 2010), (World Bank, 2018)
En los últimos 30 años, las exportaciones primarias de Paraguay muestran una especialización hacia productos agroalimentarios, con un aumento de la oferta exportadora de soja, sus manufacturas, cereales y carne bovina, y una disminución de la oferta de algodón y de madera (Enciso, 2021). Las estadísticas muestran que en el año 1991 las exportaciones agroalimentarias representaban el 40,9% de las exportaciones totales y en el 2020 ascendieron al 67%, que llega al 84% al excluir energía eléctrica (producto de mercado cautivo), cuya exportación está sujeta al Brasil. Entre los bienes agroalimentarios sobresale la soja como principal rubro de exportación, donde en los últimos cinco años los ingresos por exportación de soja representaron cerca del 40% del total agroalimentario, seguido por la carne bovina con 20% y la harina de soja con 13%, luego se ubican otros bienes con pesos relativos de un sólo dígito.
El cultivo de la soja se ubica mayormente a las orillas del Río Paraná en tres Departamentos que históricamente han concentrado casi dos tercios de la superficie total de siembra. Específicamente en la zafra 2019/2020 fue como sigue: Alto Paraná (26%), Itapuá (20%) y Canindeyú (18%) (Instituto Nacional de Biotecnología-INBIO, 2020). Otros Departamentos con importancia, para el mismo periodo fueron Caaguazú (12%) y San Pedro (10%) (Instituto Nacional de Biotecnologia, 2020).
La producción de soja en el Paraguay ha pasado de 2,7 Millones de toneladas (Mt) a mediados de los noventa a 10,0 Mt en el 2021, que en términos de superficie equivale a poco más del millón de hectáreas en 1997 a 3,5 ha en el 2020 (Cámara Paraguaya de Exportadores y Comercializadores de Cereales y Oleaginosas (CAPECO), 2020). Por su lado el rendimiento, dada la característica de clima-dependiente de la agricultura paraguaya no ha mostrado progresos tan sólidos como los dos anteriores indicadores. De hecho, al convertir la serie de tiempo 1999/1997 a 2020/2021, con base en el primero se evidencia que la mayor producción se debe a incrementos en la superficie se siembra (tasa aa 5,02) antes que, al rendimiento, cuya tasa anual acumulativa fue de 0.25. Es más, al comparar las medias de los tres años de los extremos de la serie se tiene que la superficie se incrementó 207% y el rendimiento 5%.
Es sumamente importante para la economía del país, analizar el comportamiento del cultivo de la soja, debido a que es el principal producto agrícola de exportación y el que mayor cantidad de ingresos genera. Una de las formas de evaluar tal desempeño es analizando el comportamiento de la productividad de la misma a lo largo del tiempo en los departamentos productores a través de la convergencia, lo que determinaría el comportamiento de la producción de soja en el tiempo en las áreas de producción más importantes. Lopes (2004) señaló que la convergencia es el proceso en el cual una misma variable puede presentar valores distintos entre países, ciudades o departamentos; hay varias razones para implementar el proceso de convergencia, entre ellas, se destacan las variaciones estructurales en la producción, difusión de tecnologías, la eliminación de obstáculos para el crecimiento de la producción, entre otras.
La convergencia desde la perspectiva de la ciencia económicas es la tendencia que presentan dos magnitudes de aproximarse a un mismo punto, y su uso más común es en el nivel de renta per cápita de los países. Parte de la premisa de que una variable presenta inicialmente (estado inicial) diferente valor entre dos países a lo largo del tiempo termina convergiendo es decir reduce su diferencia (Rodríguez-Gámez, 2020). Igualmente, se lo puede ver como un proceso en el que las regiones o países pobres (con menor ingreso per cápita) se igualan en el largo plazo con la dotadas de mayor ingreso per cápita (regiones o países ricos), debido a que crecen económicamente más rápido, atribuible a su vez a su menor magnitud inicial (Moncayo, 2004).
La literatura identifica dos tipos de convergencia. Por un lado, está la denominada convergencia absoluta y por la otra la convergencia condicional. El primero, se fundamenta en el trabajo de Solow quien en 1950 mostró que el ingreso per cápita de los países en el largo plazo convergen hacia un estado estacionario independiente de su condición inicial (Bracamontes Nevárez, 2008). La convergencia desde esta perspectiva asume que el funcionamiento del mercado (o la mano invisible) hace que las economías con menor renta per cápita crezcan a mayor velocidad que las de mayor renta (que también crecen, pero a una menor tasa) y converjan. Es decir que la tasa a la que crece la productividad es función únicamente de la magnitud de la productividad inicial.
La comprobación empírica de lo propuesto por Solow está dada (Barro & Sala-i-Martin, 1994), quienes a través de un modelo de crecimiento neoclásico muestran que la tasa de crecimiento de las economías converge hacia el estado estacionario homogéneo (Rodríguez-Gámez, 2020). Sin embargo, trabajos posteriores resaltaron la posible existencia de diferentes estados estacionarios en contraposición a uno homogéneo, y la necesidad de considerar el aspecto territorial en el proceso de convergencia.
La condicional por su parte, incluye variables no consideradas inicialmente. Sostiene que el ingreso per cápita de países con características estructurales similares también convergen en el largo plazo, tal como lo señaló Solow, pero y aquí la diferencia, independientemente de su estado o condición inicial (Bracamontes Nevárez, 2008). Es decir, mientras la primera sostiene que el crecimiento es función de la situación inicial, la segunda sostiene que en el proceso de convergencia pueden influenciar otras variables. Entre estas se cita el aspecto geográfico o territorial. Su inclusión en los estudios de convergencia llevó a considerar la ubicación geográfica tanto la de un territorio especifico al igual que la interacción entre territorio vecinos como objeto de estudio.
Relacionado a lo territorial están los conceptos de dependencia espacial entendida como la situación en la cual la tasa de crecimiento de una región depende de las regiones vecinas, y la heterogeneidad espacial que se da cuando el crecimiento depende de la localización (Antunes & Stege, 2020). Se considera que las regiones no están aisladas, sino interconectadas haciendo que su crecimiento este vinculado a esta situación, y más aún entre espacios adyacentes.
En este contexto, se tuvo como objetivo principal de la investigación evaluar la convergencia de la productividad de la soja en los departamentos productores de la región oriental durante el periodo 2007-2018, para lo cual se establecieron los siguientes objetivos específicos: a) Agrupar los departamentos con producción de soja en el periodo 2007-2018; b) Analizar entre los departamentos productores, la productividad que presentan; c) Verificar de forma econométrica el comportamiento de la productividad en el periodo establecido para la determinación de la existencia de convergencia espacial.
MATERIALES Y MÉTODOS
El estudio se llevó a cabo en la Región Oriental del país, abarcando los departamentos que presentaron actividad productiva de soja durante el periodo de investigación (2007-2018). Estos departamentos incluyen Concepción, San Pedro, Guairá, Caaguazú, Caazapá, Itapúa, Misiones, Paraguarí, Alto Paraná, Amambay y Canindeyú.
El tipo de investigación que se llevó a cabo fue de tipo Explicativa-longitudinal, mediante la recolección de datos secundarios, donde los datos utilizados fueron el volumen de producción total y superficie total cultivada de soja entre los años 2007 al 2018 por departamento. A partir de ahí, se generó el valor de la productividad. Se utilizaron datos extraídos de la página de la Dirección General de Estadísticas, Encuestas y Censos del Ministerio de Agricultura y Ganadería (MAG), además de libros, revistas e internet.
Análisis e interpretación de datos
El modelo y análisis de datos fue adaptado del trabajo realizado por Bastistella et al. (2019), donde se analizó la convergencia de productividad de la soja en Río Grande do Sul, en el cual, se habló de que los modelos econométricos lineales no comprenden los efectos que son incorporados por los modelos espaciales, como lo son la dependencia y heterogeneidad espacial.
Siguiendo con el trabajo de Bastistella et al. (2019), se desarrolló un modelo econométrico específicamente para controlar la influencia que tiene la proximidad espacial en los datos. Esta dependencia espacial se manifiesta debido a las relaciones entre las ubicaciones geográficas y se abordó en el modelo mediante una variable que refleja esta relación a lo largo del espacio. Cuando un modelo teórico o empírico muestra esta influencia espacial, se sugiere emplear un enfoque que pueda capturar y considerar este efecto espacial presente en los datos.
Con la finalidad de comprobar el test en el cual se plantea si existe o no convergencia absoluta, se estimó el modelo con base a lo realizado por Bastistella et al. (2019), que se presenta a continuación:
Donde
es el intercepto que se presenta, la variable independiente es el logaritmo natural de la productividad de la soja en el departamento i y en el periodo t, y el corresponde al error aleatorio del modelo.La
es la variable dependiente y está dada por la tasa de crecimiento de la producción de soja, la misma, será calculada por el logaritmo natural de la división entre los valores del rendimiento promedio de la producción (kg ha-1) de soja en el periodo final dividido por esa misma variable en su periodo inicial:
RESULTADOS Y DISCUSIÓN
A continuación, se procede al análisis de los resultados, los cuales buscan probar la hipótesis de convergencia absoluta de la productividad de la soja, entre los departamentos productores de la región oriental del país, durante el período de 2007 a 2018 y responder a los objetivos de investigación.
El análisis de la productividad promedio de la soja en distintos departamentos revela variaciones significativas en los rendimientos por hectárea (Tabla 1). Caaguazú se destaca con la productividad más alta, registrando un promedio de 2717.47 kg ha-1, seguido de Canindeyú (2655.14 kg ha-1) y Amambay (2625.20 kg ha-1). Por otro lado, Paraguarí muestra el rendimiento más bajo con un promedio notablemente inferior de 813.58 kg ha-1. Estas diferencias en la productividad entre los departamentos productores sugieren disparidades en las condiciones de cultivo o en las estrategias agrícolas adoptadas en cada región.
Tabla 1. Promedio de la productividad (en kg ha-1) de la Soja en los distintos departamentos productores.
| Departamentos | Productividad (t) |
| Concepción | 2547,08 |
| San Pedro | 2477,18 |
| Guairá | 2437,94 |
| Caaguazú | 2717,47 |
| Caazapá | 2439,63 |
| Itapúa | 2637,08 |
| Misiones | 2187,13 |
| Paraguarí | 813,58 |
| Alto Paraná | 2558,15 |
| Amambay | 2625,20 |
| Canindeyú | 2655,14 |
Fuente: Elaborado con los datos obtenidos del volumen de producción y la superficie sembrada de soja desde el año 2007 al 2018 de la Dirección General de Estadísticas, Encuestas y Censos del Ministerio de Agricultura y Ganadería (MAG)
La forma más común de probar la hipótesis de convergencia absoluta es asociar el nivel inicial de productividad del cultivo con el aumento de esta misma productividad a lo largo del tiempo. De acuerdo con el modelo neoclásico desarrollado por Solow (1956), citado en (Batistella et al. 2019), si todas las regiones, departamentos o incluso municipios convergen al mismo nivel, se debe observar una relación negativa entre el crecimiento de la productividad y su nivel inicial durante el período.
Tabla 2. Primera estimación con modelos de MCO (Mínimos Cuadrados Ordinarios) para verificar la hipótesis de convergencia absoluta.
| Variable Dependiente | |
| Constante | 0 .4285977 (0.003945856) |
| PROD (2007) | - 0.0001033 (0.0001582) |
El test de los Mínimos Cuadrados Ordinarios (MCO), que se muestra en la Tabla 2, se utiliza para estimar el modelo econométrico espacial (Almeida, 2012).
Tabla 3. Test de verificación.
| TEST | VALORES |
| AIC | 218.226 |
| SC | 223.150 |
| ML - Error | 3.1713 |
| (0.06010) | |
| ML - Error | 1.2165 |
| (0.02003) | |
| I de Moran | 1.8440 |
| (0.01751) | |
| Test Jacque-Bera | 2.886 |
| (0.2362) | |
| Multicolinealidad | 5.762580 |
Fuente: Elaborada con los resultados obtenidos a través del Software Stata 16.
El Índice de Moran, que se muestra en la Tabla 3, es una medida estadística desarrollada por Alfred Moran (1950), este test analiza las variaciones de autocorrelación espacial entre valores vecinos más cercanos, y estos pueden clasificarse como positivo, negativo y sin autocorrelación espacial(cero).
El mismo autor afirma que, este test consiste en la medición de la presencia o ausencia de autocorrelación espacial de una variable. Para verificar el nivel de significancia se utiliza de referencia el valor de 0.05, si el valor de la probabilidad p es menor que o igual a 0.05, se pudo afirmar que sí existe autocorrelación espacial. Así mismo, se verificó la existencia de autocorrelación espacial de los errores de regresión, es decir, indican la presencia de dependencia espacial para el cultivo de soja. El valor estadístico del índice de Moran es 1.8440, a un nivel de significancia del 1%.
De esta forma, basándose en el resultado arrojado por este test, se demostró que las variables están espacialmente autocorrelacionadas indicando la presencia de dependencia espacial, al igual que en Batistella et. al. (2019), que obtuvieron el valor de 1,8990 con un nivel de significancia del 5%, en comparación al valor obtenido en este estudio.
Con la estimación se demostró que las variables están espacialmente auto correlacionadas, a partir de ahí, se analizaron los valores de los Multiplicadores de Lagrange (ML), con el fin de comprobar cuál es la mejor especificación espacial del modelo. Los multiplicadores de Lagrange se utilizan para detectar el desfase espacial de la variable dependiente (Almeida, 2012). ML y MLR son pruebas de multiplicador de Lagrange contra la autocorrelación espacial en forma de modelo SEM (Almeida, 2012). Se verificó que en los test de ML y MLR, en el cuadro 3, que el modelo más adecuado es el Modelo de Error Espacial (SEM) por máxima verosimilitud, Almeida (2012), menciona, que este estimador es considerado el más factible para muestras pequeñas.
El Test Jarque-Bera, cuantifica qué tanto se desvían los coeficientes de asimetría de los esperados en una distribución normal. A través del test de Jarque-Bera, es posible identificar los problemas de no normalidad de los residuos, esto concuerda con el trabajo hecho por (Batistella et al. 2019) y (Almeida 2012). Para verificar el test se utilizó de referencia el valor de 0.05, si JB es mayor que este valor, se rechaza la hipótesis de normalidad. El resultado obtenido, que se muestra en el Cuadro 3, indicó que no hay evidencia de que los residuos siguen una distribución normal.
El valor obtenido del test de Multicolinealidad fue inferior a 30, (Tabla 3), lo que indicó que no existe problema de colinealidad, como lo expresa (Guyarati y Porter, 2010). Guyarati y Porter (2010), mencionan que la AIC y SC (Criterio de Información de Akaike y de Schwarz), son pruebas de bondad del ajuste del modelo estimado, según estos criterios, cuanto más bajo sea el valor de estos estadísticos, mejor será el modelo, estos test se muestran en la tabla 3.
Estas estimaciones también fueron realizadas por Batistella et al. (2019) alcanzando los mismos resultados expuestos. De esta forma, para controlar el problema de no normalidad de residuos, resultado arrojado por el test Jarque-Bera, según Almeida (2012), el modelo SEM se debió estimar mediante el método de momentos generalizados (MGM, en el que las estimaciones de los errores estándar son robustas a la dependencia espacial entre los términos de error.
Este problema de no normalidad de residuos concordó con el trabajo de Batistella et. al. (2019), el cual, utilizaron el modelo SEM, estimado por MGM para controlar dicho problema, según lo recomendado por Almeida (2012).
Tabla 4. Estimación del Modelo de Error Espacial, estimado por Método de Momentos Generalizados para hipótesis de convergencia absoluta.
| Variable Dependiente | |
| Constante | 0 .4267777 (0.003945856) |
| PROD (2007) | - 0.0000923 (0.0001362) 0.11346722 (0.061496) |
Fuente: Elaborada con los resultados obtenidos a través del Software Stata 16.
La tabla 4, muestra la estimación del modelo SEM, según el método MGM. Batistella et al. (2019) menciona que, el modelo SEM tiene la característica de presentar la dependencia espacial en el término de error de regresión, en otras palabras, el patrón espacial manifestado en el término de error está dado por efectos no modelados.
El efecto marginal sobre la variable dependiente variable PROD INICIAL (2007) (-0.0000923), se observa en el cuadro 4, este resultado mostró significancia estadística y signo negativo, como se esperaba, indicando la presencia de autocorrelación, esto indicó que la variable dependiente está influenciada por el impacto de todos los departamentos, siendo los departamentos más cercanos los más influenciados, produciéndose de manera decreciente.
Los departamentos que tienen alta productividad influyen tanto en su crecimiento como en el de los departamentos vecinos. Además, se detectó la dependencia espacial a través de los residuos, esto indicó la existencia de factores no modelados pueden influir en este proceso, esto coincidió con lo expuesto anteriormente por Batistella et al. (2019).
El resultado obtenido indicó que sí hubo un proceso de convergencia absoluta de la productividad de la soja entre los departamentos productores de la región oriental de Paraguay durante el periodo comprendido entre el 2007 al 2018. Este resultado no difirió al obtenido en Batistella et. al. (2019), en el cual la convergencia fue evaluada en las microrregiones del estado de Rio Grande do Sul. Lo mismo sucedió al comparar este resultado, con el obtenido en Simões de Almeida, Salgueiro Perobelli y Costa Ferreira (2008) y el de Pelinski et. al. (2016); los cuales evaluaron la convergencia de la productividad agropecuaria en el sur de Brasil, obteniendo un mismo resultado a favor de la existencia de convergencia.
CONCLUSIÓN
Considerando la importancia de la soja en el Paraguay, el objetivo del presente estudio fue evaluar la convergencia de la productividad de la soja en los departamentos productores de la región oriental durante el periodo 2007-2018 probando la hipótesis de convergencia absoluta de la productividad de este cultivo. Se estima el modelo de convergencia mediante técnicas de econometría espacial.
El estudio presenta evidencia a favor de la existencia de convergencia absoluta de la productividad de la soja a través de los departamentos productores de la región oriental del país durante el periodo comprendido entre el 2007 al 2018, debido que el resultado obtenido presenta significancia estadística.
Junto con eso, se comprueba que el aumento de la productividad de un departamento, influyen en el aumento de la productividad de los departamentos vecinos, de esta manera se verifica la existencia de una dependencia espacial entre los mismos. Siendo así, se considera que Caaguazú, Canindeyú, Amambay, Itapúa y Alto Paraná al ser los departamentos con mayor productividad, influyen de manera positiva en los demás.
Siendo positiva la presencia de convergencia absoluta en las pruebas, la misma indica un escenario favorable para la agricultura del país, porque permite distinguir eficiencias productivas cada vez mayores y la existencia de dependencia espacial entre los departamentos indica que las ganancias en términos de políticas no se limitan a unos pocos departamentos, si no que se amplía a los departamentos contiguos.
Cabe destacar, que una de las limitaciones de este estudio es la falta de datos para el estudio de la hipótesis de convergencia condicional; de este modo, se determinaría que tanto influyen las variables, producción inicial, nivel de educación, tipo de suelo, uso de insumos agrícolas, número de maquinarias e implementos, en el aumento de la productividad del cultivo.
Se recomienda para posteriores trabajos, evaluar la hipótesis de convergencia condicional de la productividad de la soja en la región oriental, así también, se sugiere determinar la convergencia absoluta y condicional entre municipios de un determinado departamento, el cual se destaque en la producción de este cultivo.