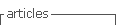INTRODUCCIÓN
Las características higroscópicas de la madera están relacionadas con su capacidad para absorber o expulsar agua en el intervalo que va desde un estado seco de la madera hasta un estado saturado (Sotomayor-Castellanos y Ramírez-Pérez, 2013). Lo anterior se asocia a tres propiedades básicas del material: la variabilidad de la madera, que se refiere a las diferencias encontradas en la magnitud de los parámetros físicos entre especies y árboles; la anisotropía, que se refiere a la diferencia en la magnitud de las características físicas que depende de la dirección de medición, y por último, la heterogeneidad, que se manifiesta como la desigualdad en la magnitud de las características físicas, y depende de su posición relativa en el plano leñoso y de acuerdo a las diferentes escalas de observación en su organización jerárquica.
Entre los productos de madera donde el conocimiento de las características higroscópicas de una especie de madera encuentra aplicación, se pueden citar muebles, instrumentos musicales, madera de ingeniería y tableros contrachapados y aglomerados, y otros materiales de Ingeniería reconstituidos a partir de madera como materia prima. Respecto a la industria de la edificación con madera, las características físicas encuentran aplicación en el dimensionado de elementos estructurales, como vigas y columnas, y en componentes de construcciones de madera como lo son vigas laminadas, escaleras, cubiertas, muros y entramados (Şenol y Budakç, 2016).
En el densificado higromecánico de la madera se han identificado tres mecanismos para mantener la deformación permanente (Morsing y Hoffmeyer, 1998). El primero evita que la madera se vuelva a suavizar al modificar de manera artificial la higroscopicidad de la pared celular y, por lo tanto, ocasiona que la pared celular sea inaccesible al agua. El segundo forma enlaces cruzados covalentes entre los componentes de la madera en el estado deformado; y finalmente, el tercero relaja las tensiones almacenadas durante el densificado en las microfibrillas y los polímeros de la matriz ligno-celulósica de la madera.
Por su parte, Navi y Heger (2004) propusieron dos fenómenos responsables de la estabilidad geométrica en la madera densificada. En el primero, la transformación de la lignina de un estado plástico a vítreo y la alteración de los enlaces secundarios dentro de la matriz de lignina restringen las microfibrillas de celulosa deformadas. En el segundo fenómeno, cuando se elimina el agua, la formación de enlaces de hidrógeno entre las hemicelulosas y la celulosa tiene como efecto la consolidación de las microfibrillas de celulosa deformada.
Cuando la madera densificada se expone a la humedad, tiende a recuperar su forma original (Şenol y Budakç, 2016). La recuperación geométrica de la madera densificada no es sinónimo de la higroexpansión de la madera. En el caso de la madera densificada, es el resultado de la acción de la humedad, combinada con el efecto de la liberación de esfuerzos creados durante el secado, calentamiento y deformación propios del densificado (Navi y Heger, 2004). Las técnicas de densificado de la madera se dirigen para diversificar usos de especies con poco aprovechamiento industrial y de baja densidad (Rademacher et al., 2017; Yan et al., 2020). Sin embargo, el densificado de maderas puede ampliar el uso de especies con alta densidad y es una tendencia contemporánea en ciencia y tecnología de la madera (Sikora, Gaffová, Rajnoha, Šatanová y Kminiak, 2017; Laskowska, 2020).
Si al densificado de la madera se agregan tratamientos estabilizadores, sus propiedades higroscópicas se mejoran (Kutnar y Šernek, 2007) y su estabilidad dimensional se incrementa ((Popescu, Lisa, Froidevaux, Navi y Popescu., 2014). Con el propósito de reducir la recuperación geométrica de la madera densificada se aplican tratamientos de impregnación con resinas sintéticas, ceras y monómeros de vinil (Khalil et al., 2014; Pelit y Emiroglu, 2020; Schwarzkopf, 2020). En el mismo sentido, existe evidencia empírica de que el densificado de la madera modifica sus características higroscópicas (Khalil et al., 2014; Hajihassani, Mohebby, Najafi y Navi, 2018). Sin embargo, las magnitudes son diferentes para cada especie.
Los objetivos de este trabajo fueron determinar las recuperaciones geométricas de madera densificada y calcular las higroexpansiones radiales de la madera sólida de ocho especies mexicanas: Cupressus lindleyi Klotzsch ex Endl., Cedrela odorata L., Swietenia macrophylla King, Tabebuia donnell-smithii Rose, Fraxinus uhdei (Wenz.) Lingelsh, Fagus mexicana Martínez, Dalbergia palo-escrito Rzed. & Guridi-Gómez, y Guazuma ulmifolia Lam.
MATERIALES Y MÉTODOS
Se adquirieron piezas de madera aserrada de C. lindleyi, C. odorata, S. macrophylla, T. donnell-smithii, F. uhdei, F. mexicana, D. palo-escrito y G. ulmifolia. De cada especie se prepararon dos grupos de probetas libres de irregularidades de crecimiento y orientadas en las direcciones radial, tangencial y longitudinal. El primer grupo consistió en 18 probetas de madera sin densificar con dimensiones de 0,02 m × 0,02 m × 0,06 m. El segundo grupo fue de 18 probetas de madera densificada con dimensiones de 0,014 m × 0,02 m × 0,06 m. Las probetas densificadas provienen del material experimental reportado por Sotomayor-Castellanos, Adachi, Iida y Hayashi (2019). Antes y después del densificado las probetas se almacenaron en una cámara de climatización fabricada en el Laboratorio de Mecánica de la Madera de la Facultad de Ingeniería en Tecnología de la Madera, de la Universidad Michoacana de San Nicolás de Hidalgo, México, con temperatura de 20 °C y humedad relativa del aire de 65 % hasta que alcanzaron un peso constante.
El tratamiento de densificado siguió el protocolo reportado por Sotomayor-Castellanos et al. (2019) y consistió en cuatro pasos: 1) en grupos de cuatro, las probetas se colocaron entre dos placas térmicas, con dimensiones de 1 m × 1 m, de una prensa Shon ai-Tekko, Modelo TS-100 (Tokio, Japón), con capacidad de 100 T; 2) las probetas de espesor inicial de 0,02 m se comprimieron en la dirección radial hasta alcanzar un espesor final de 0,014 m, equivalente a 70 % de su dimensión original, que representa un coeficiente de densificado objetivo de 30 % (Blomberg, Persson y Blomberg, 2005). La presión aplicada varió de 30 MPa 50 MPa, dependiendo de la densidad de la madera; 3) las probetas en la prensa se calentaron a 120 °C durante 6 h; 4) las probetas fueron retiradas de la prensa y enfriadas a temperatura de laboratorio (20 °C) durante 12 h. La Figura 1 presenta probetas densificadas y sin densificar antes del procedimiento de humidificación de F. uhdei y F. mexicana.

Figura 1 Probetas densificadas y sin densificar antes de su humidificación. a) Fraxinus uhdei densificada; b) Fraxinus uhdei sin densificar; c) Fagus mexicana densificada; d) Fagus mexicana sin densificar.
El procedimiento de humidificación también siguió el protocolo reportado por Sotomayor-Castellanos, Tinoco-Campos y Raya-González (2020) y consistió en cuatro pasos: 1) se pesaron y midieron las dimensiones de las probetas con un contenido de humedad inicial de equilibrio con las condiciones de la cámara de climatización; 2) se sumergieron en agua a temperatura de 23 °C durante 72 h para lograr un contenido de humedad, mayor que el punto de saturación de la fibra. En este estado de humedad se pesaron y se midieron nuevamente las dimensiones de las probetas; 3) se secaron en un horno a una temperatura de 103 °C durante 72 h; 4) en el estado seco las probetas se pesaron y se midieron sus dimensiones. Los contenidos de humedad se calcularon con la relación peso/volumen correspondiente al momento de las pruebas de acuerdo a la Organización Internacional de la Normalización (ISO, por sus siglas en inglés; International Organization for Standardization) (ISO, 2014a). Las densidades se determinaron con las relaciones entre el volumen de la madera y su peso seco (ISO, 2014b). La Figura 2 esquematiza las dimensiones de las probetas durante el procedimiento de humidificación.
La recuperación geométrica de la madera densificada se calculó con la fórmula (1) (Bao et al., 2017):
Donde:
RG = Recuperación geométrica (%)
Rsat = Dimensión radial de la probeta en estado saturado (m)
Rsec = Dimensión radial de la probeta en estado seco (m)
Rini = Dimensión radial de la probeta en estado inicial (m)
Rden = Dimensión radial de la probeta después densificado (m)
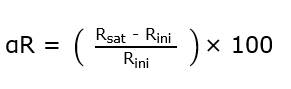
La higroexpansión de la madera sin densificar se calculó con la fórmula (2) (Bao et al., 2017):
Donde:
αR = Higroexpansión radial (%)
Rsat = Dimensión radial de la probeta en estado saturado (m)
Rini = Dimensión radial de la probeta en estado inicial (m)
La estrategia experimental se orientó hacia la comparación de resultados entre especies y entre pares de muestras correspondientes a la madera densificada y sin densificar. Las variables de entrada fueron para la madera densificada: los valores promedios del contenido de humedad, la densidad y la recuperación geométrica medidos en cada una de las 18 probetas de las ocho especies. De manera análoga para la madera sin densificar, las variables de salida fueron los valores promedio del contenido de humedad, la densidad y la higroexpansión radial. De tal forma, se formaron seis muestras independientes; se realizaron pruebas de normalidad y de verificación, así como análisis de varianza. El criterio de demarcación para aceptar una distribución normalmente distribuida fueron valores del sesgo estandarizado (SE) y del apuntamiento estandarizado (AE) al interior del intervalo: [- 2, + 2]. Se verificó la hipótesis nula H0: μ1 + μ2 = 0, donde μ1 representa las medias de las muestras de madera densificada y μ2 representa las medias correspondientes a la madera sin densificar. Todas las pruebas estadísticas se efectuaron para un nivel de confianza de 95 % con el programa Stagraphics Centurion XV. Así, el criterio de demarcación para aceptar una diferencia estadísticamente significativa fue un valor de P(α = 0,05) < 0,05.
RESULTADOS Y DISCUSIÓN
Las pruebas de normalidad indican que las distribuciones de todas las muestras estudiadas son normales (Tabla 1). Para los pares de muestras del contenido de humedad y de la densidad, las pruebas de verificación de varianzas no indican diferencias significativas. Estos resultados validan la homogeneidad de las mediciones entre especies y entre pares de muestras correspondientes a la madera densificada y la madera sin densificar. En cambio, para las recuperaciones geométricas versus las higroexpansiones radiales, las pruebas indican una diferencia significativa. Además, para los tres pares de muestras, el análisis de varianza indica diferencias significativas, corolario que muestra el efecto del densificado de la madera sobre sus densidades, contenidos de humedad y variaciones dimensionales.
Tabla 1 Resultados pruebas estadísticas.
| Madera densificada | Madera sin densificar | |||||
| SE | AE | SE | AE | Ver-var | Anova | |
| [- 2, + 2] | [- 2, + 2] | [- 2, + 2] | [- 2, + 2] | P(α = 0,05) | P(α = 0,05) | |
| CH | - 1,2910 | 0,9524 | 0,3291 | - 0,2687 | 0,355* | < 0,001# |
| ρCH | - 0,6365 | - 0,5099 | - 0,5182 | - 0,0822 | 0,452* | 0,001# |
| RG | - 0,8019 | - 0,2741 | - | - | 0,002# | < 0,001# |
| αR | - | - | 0,7311 | - 0,2853 | - | - |
SE = Sesgo estandarizado; AE = Apuntamiento estandarizado; Ver-var = Verificación de varianza; Anova = Análisis de varianza; CH = Contenido de humedad; ρCH = Densidad; RG = Recuperación geométrica; αR = Higroexpansión radial; *P(α = 0,05) > 0,05: no existe diferencia significativa; #P(α = 0,05) < 0,05: existe diferencia significativa.
Para las ocho especies, desde el estado inicial de la madera densificada hasta su estado saturado, el contenido de humedad se incrementó en promedio 53,1 %. En cambio, para la madera sin densificar el aumento fue de 49,8 % (Tabla 2). El coeficiente de variación del contenido de humedad de la madera densificada incrementó 116 % respecto al de la madera sin densificar. En el mismo contexto, la densidad de la madera fue 33 % mayor en comparación con la densidad de la madera sin densificar (Tabla 2). Empero, para estos parámetros sus coeficientes de variación fueron similares. En la madera densificada no se observaron fisuras o zonas con madera comprimida en exceso, lo que permite inducir que el tratamiento de densificado fue uniforme y eficiente, por lo que sus propiedades físicas y mecánicas pueden mejorarse (Laine et al., 2014; Sotomayor-Castellanos et al., 2019).
Tabla 2 Contenidos de humedad, densidades, recuperaciones geométricas e higroexpansiones radiales.
| Madera densificada | Madera sin densificar | ||||||
| CH | ρCH | RG | CH | ρCH | αR | ||
| Especies | (%) | (kg/m3) | (%) | (%) | (kg/m3) | (%) | |
| Cupressus lindleyi | μ | 6,5 | 607 | 55 | 8,7 | 446 | 1,8 |
| σ | 1,0 | 55 | 8,9 | 0,8 | 30 | 0,9 | |
| Cedrela odorata | μ | 8,0 | 646 | 57 | 8,9 | 514 | 2,9 |
| σ | 2,6 | 121 | 4,9 | 1,5 | 101 | 0,9 | |
| Swietenia macrophylla | μ | 7,0 | 735 | 41 | 8,7 | 531 | 2,4 |
| σ | 0,7 | 43 | 8,5 | 0,7 | 37 | 1,0 | |
| Tabebuia donnell-smithii | μ | 6,7 | 791 | 65 | 8,4 | 604 | 2,6 |
| σ | 0,5 | 48 | 3,9 | 0,7 | 32 | 0,7 | |
| Fraxinus uhdei | μ | 7,1 | 807 | 78 | 9,5 | 621 | 2,8 |
| σ | 0,6 | 41 | 5,4 | 0,9 | 40 | 1,4 | |
| Fagus mexicana | μ | 7,6 | 854 | 77 | 9,7 | 631 | 3,9 |
| σ | 0,5 | 44 | 3,4 | 1,1 | 25 | 2,0 | |
| Dalbergia palo-escrito | μ | 5,2 | 866 | 29 | 8,1 | 614 | 1,8 |
| σ | 0,6 | 91 | 5,8 | 1,1 | 83 | 0,7 | |
| Guazuma ulmifolia | μ | 7,7 | 913 | 72 | 9,0 | 699 | 4,3 |
| σ | 1,8 | 54 | 2,2 | 0,5 | 53 | 1,9 | |
| Ocho especies | μ | 7,0 | 777 | 59,3 | 8,9 | 583 | 2,8 |
| Ocho especies | CV | (13) | (14) | (30) | (6) | (14) | (32) |
CH = Contenido de humedad; ρCH = Densidad; RG = Recuperación geométrica; αR = Higroexpansión radial; μ = Media; σ = Desviación estándar; CV = Coeficiente de variación en porciento y entre paréntesis.
Después de su humidificación, las probetas densificadas mostraron una recuperación radial geométrica promedio de 59,3 % (Tabla 2). Este resultado es efecto del incremento del contenido de humedad desde el estado inicial de la madera densificada de 7 %, hasta su estado saturado en promedio de 60,1 % y es comparable a los reportados por Schwarzkopf (2020) con coeficientes de compresión entre 55 % y 66 %. Para madera de Fagus sylvatica reporta una recuperación geométrica de 34 %, para Populus spp. de 67,5 % y para Picea abies de 65,8 %. No obstante, debido a las diferencias de tiempo, presión y temperatura entre los tratamientos de densificado, es difícil comparar resultados entre reportes publicados (Pelit, Sönmez y Budakçı, 2014; Şenol y Budakç, 2016; Sadatnezhad, Khazaeian, Sandberg y Tabarsa., 2017; Pelit, Budakçi y Sönmez, 2018; Pertuzzatti et al., 2018; Pelit y Yorulmaz, 2019; Pelit y Emiroglu, 2020).
Para la madera sin densificar, el contenido de humedad promedio de todas las especies se incrementó desde 8,9 % hasta 57,8 %. Así, el efecto de la humedad retenida en la madera se manifiesta en el aumento del espesor de las probetas y se evalúa con la higroexpansión radial cuyo promedio fue de 2,8 % (Tabla 2). El coeficiente de variación promedio de la higroexpansión radial de la madera sin densificar fue más del doble respecto al coeficiente de variación de la recuperación geométrica de la madera densificada (Tabla 2). El coeficiente de variación de la higroexpansión radial de la madera sin densificar es mayor en 6 % en comparación con el coeficiente de la recuperación geométrica de la madera densificada.
Las recuperaciones geométricas y las higroexpansiones radiales correspondientes a cada especie indican una tendencia a incrementarse a medida que la densidad de la madera aumenta (Tabla 2 y Figura 3). Sin embargo, los resultados de S. macrophylla y D. palo-escrito se apartan de esta tendencia y C. odorata tuvo un aumento mayor. Para las recuperaciones geométricas, el coeficiente de determinación R2 = 0,05 de la correlación lineal para las ocho especies RG = 0,034 8 ρCH + 32,26 se incrementa a R2 = 0,75 con una correlación RG = 0,0718 ρCH + 12,25 si no se contabilizan los valores de S. macrophylla y D. palo-escrito. Igualmente, para las higroexpansiones radiales, el coeficiente R2 = 0,46 de la correlación αR = 0,0075 ρCH - 1,58, se incrementa a R2 = 0,79, si se evitan los resultados de estas dos especies, con la correlación αR = 0,0095 ρCH - 2,66.
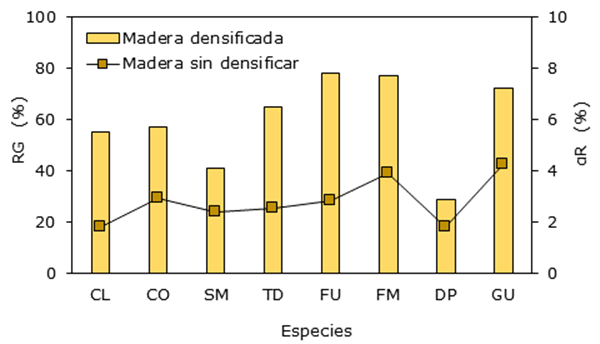
Figura 3 Recuperación geométrica e higroexpansión de las especies. RG = Recuperación geométrica; αR = Higroexpansión radial. CL= Cupressus lindleyi; CO = Cedrela odorata; SM = Swietenia macrophylla; TD = Tabebuia donnell-smithii; FU = Fraxinus uhdei; FM = Fagus mexicana; DP = Dalbergia palo-escrito; GU = Guazuma ulmifolia.
El intervalo de recuperaciones geométricas va desde un mínimo de 29 % para D. palo-escrito hasta un máximo de 78 % correspondiente a F. uhdei (Tabla 2). Este resultado es comparable con el reportado por Kutnar y Kamke (2012) quienes obtuvieron para madera de Populus deltoides × Populus trichocarpa, con densidad de 389 kg/m3 y densificada a un coeficiente de densificado de 66 %, una recuperación geométrica de 75 %. Así mismo, los resultados son comparables a los de Sotomayor-Castellanos (2017) quien reportó para madera de Gyrocarpus americanus, densificada a una tasa de 50 % con una metodología similar a la de esta investigación, una recuperación geométrica de 62,2 % (CV = 8,7 %). Asimismo, Bao et al. (2017) registraron para madera densificada una recuperación geométrica de 80 %, ocasionada por un coeficiente de densificación de 50 % para Populus tomentosa con densidad de 390 kg/m3.
Los valores medios de las higroexpansiones radiales de las maderas estudiadas (Tabla 2) van desde un mínimo de 1,8 % correspondientes a C. lindleyi y D. palo-escrito hasta un máximo de 3,9 % para F. americana. Estos resultados son similares a los de Sotomayor-Castellanos (2016) quien, empleando una metodología de humidificación similar a la de esta investigación, publica una higroexpansión radial de 3,5 % (CV = 21 %) para madera de Pinus pseudostrobus, con densidad de 408 kg/m3. Igualmente, Sotomayor-Castellanos, Ávila-Calderón y Fuentes-Salinas (2021) informaron para madera de Spathodea campanulata, con densidad de 269 kg/m3, una higroexpansión radial de 4,44 % (CV = 28 %); para Fraxinus americana, con densidad de 534 kg/m3, una higroexpansión radial de 2,41 % (CV = 19 %); y para Albizia plurijuga, con densidad de 597 kg/m3, una higroexpansión radial de 2,47 % (CV = 25 %).
Por su parte, Shukla y Kandem (2010) reportaron para maderas tropicales las higroexpansiones radiales siguientes: Triplochiton scleroxylon 2,1 %, Nauclea diderrichii 3,5 %, Guibourtia tessmannii 4,2 %, Chlorophora excelsa 2,2 %, Mimusops heckelii 3,7, Baillonella toxisperma 1,8 %, Distemonanthus benthamianus 2,2 %, Tectona grandis 1,2 % y Microberlinia brazzavillensis 1,6 %, magnitudes similares a los resultados de esta investigación (Tabla 2).
La literatura sobre las características higroscópicas de la madera indica una importante variabilidad en las magnitudes de los parámetros, las cuales son particulares a cada estudio. Así, el fenómeno de la higroexpansión de la madera es explicado combinando diferentes puntos de vista. Un primer argumento es la interacción, a nivel molecular y de fibrillas, entre los diferentes componentes químicos de la madera y la humedad. De esta forma, se producen los fenómenos de absorción-adsorción de fluidos en el tejido ligno-celulósico (O´leary y Hodges, 2001; Berry y Roderick, 2005; Repellin y Guyonnet, 2005; Sahin, 2010; Patera, Derome, Griffa y Carmeliet, 2013).
Un segundo enfoque explicativo es el acomodo y forma anatómica de la estructura jerárquica a nivel de pared celular, de una célula, de una capa de crecimiento que considere un volumen elemental de materia (Rafsanjani et al., 2014; Joffre et al., 2016; Derome, Zhang, Chen y Carmeliet, 2018; Chiniforush, Akbarnezhad, Valipour y Malekmohammadi, 2019; Fu, Cloutier, Laghdir y Stevanovic, 2019). De tal forma, el fenómeno de compresión-recuperación de la madera es resultado de su estructura celular y de las propiedades de los polímeros de la pared celular (Kutnar y Kamke, 2012).
Conviene destacar que es poco probable que las condiciones de uso final de la madera densificada incluyan su inmersión en agua durante mucho tiempo. Por esta razón, las aplicaciones de los resultados de esta investigación se limitan a sus condiciones experimentales. Para su aplicación en diseño ingenieril y en nuevas aplicaciones técnicas, es recomendable realizar investigaciones intensivas de las maderas estudiadas en condiciones similares a las de uso industrial.
Debido a los diferentes coeficientes de densificado reportados y a la variedad de especies examinadas en la literatura, los resultados de la recuperación geométrica son difíciles de comparar con estudios precedentes. Los parámetros aquí obtenidos son útiles principalmente como referencia y desde un enfoque comparativo entre el potencial para el densificado a nivel industrial de las maderas estudiadas. En cambio, los valores promedio de higroexpansiones radiales aquí determinados son comparables a los reportados en la bibliografía para maderas con rangos de densidad semejantes.
CONCLUSIONES
Los valores promedio de la recuperación geométrica y de la higroexpansión radial de las maderas C. lindleyi, C. odorata, T. donnell-smithii, F. uhdei, F. mexicana, y G. ulmifolia aumentan a medida que sus densidades se incrementan. En cambio, para S. macrophylla y D. palo-escrito, la recuperación geométrica y la higroexpansión radial son menores comparativamente a las otras especies
Para las ocho especies estudiadas la recuperación geométrica de la madera densificada es mayor que la higroexpansión radial de la madera sin densificar. En sentido opuesto, el coeficiente de variación de la recuperación geométrica de la madera densificada es menor respecto al de la madera sin densificar.