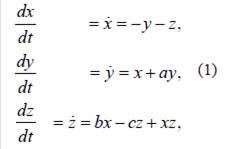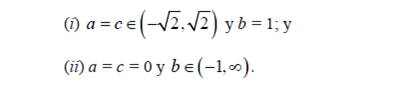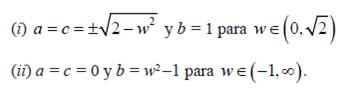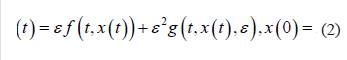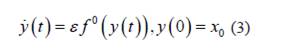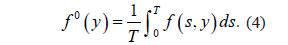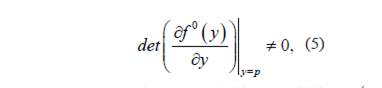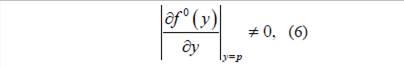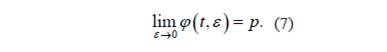Introducción
Una bifurcación del tipo cero-Hopf en ℝ 3 es un despliegue de dos parámetros de un sistema diferencial autónomo tridimensional con un punto de equilibrio cero-Hopf, esto es, el despliegue tiene un punto de equilibrio aislado con un valor propio cero y un par de valores puramente imaginarios. El sistema Rössler, es un sistema que bajo ciertas condiciones se da la bifurcación del tipo cero-Hopf, estos sistemas se crearon para estudiar la existencia de atractores extraños en dimensión tres.
El objetivo principal del presente artículo, es estudiar la teoría del promedio para calcular las órbitas periódicas que bifurcan de un punto de equilibrio cero-Hopf en los sistemas Rössler.
La teoría del promedio es una herramienta clásica y madura para estudiar el comportamiento de la dinámica de sistemas diferenciales no lineales, y en particular sus órbitas periódicas. Esta técnica de promediar convierte el problema de encontrar órbitas periódicas de los sistemas diferenciales, en encontrar ceros de algunas funciones adecuadas de dimensión tres. Este método aparte de proporcionar condiciones sobre los parámetros y también sobre los niveles de sistema Rössler, los cuales garantizan la existencia de soluciones periódicas; también proporciona estimaciones analíticas de la forma de estas órbitas periódicas.
La estructura que da sustento teórico al trabajo se presenta en cinco secciones que están relacionadas entre sí; considerando como principal, la sección que menciona la teoría del promedio y el teorema que hace referencia a la aplicación de la misma. En particular, se estudia la aplicación de esta teoría en el sistema diferencial Rössler para el cálculo de sus órbitas periódicas a partir de una bifurcación del tipo cero-Hopf.
Finalmente, en la última sección “Resultados” se mencionan los teoremas que nos dicen cuándo los sistemas Rössler produce alguna órbita periódica a partir de un equilibrio cero-Hopf, aplicando la teoría del promedio.
Materiales y métodos
La realización de este artículo se fundamenta en el análisis bibliográfico a través de la revisión de materiales existentes con respecto al cálculo de órbitas periódicas mediante la teoría del promedio, de modo a entender la aplicación de esta técnica en sistemas diferenciales.
Resultados y Discusión
Sistema de Rössler
Se considera el sistema diferencial de ecuaciones:
formado por tres ecuaciones diferenciales ordinarias no lineales, introducido en (Rossler,1976), ver también en (Scott, 2006).
Es importante notar que tanto las órbitas periódicas como toda la dinámica del sistema dependen de sus tres parámetros 𝑎, 𝑏 y ??.
Puntos de equilibrio del sistema de Rössler
Los puntos de equilibrio de este sistema son:
𝑃 1 = −(𝑎𝑏−𝑐), (𝑎𝑏−𝑐) 𝑎 ,− (𝑎𝑏−𝑐) 𝑎 y 𝑃 2 =(0,0,0). Estos puntos de equilibrio se obtienen igualando las ecuaciones del sistema (1) a cero y trabajando algebraicamente, esto es:
−𝑦−𝑧=0, →𝑦=−𝑧,
𝑥+𝑎𝑦=0, →𝑥=𝑎𝑧,
𝑏𝑥−𝑐𝑧+𝑥𝑧=0, →𝑎 𝑧 2 + 𝑎𝑏−𝑐 𝑧=0,
se resuelve esta última igualdad y se obtiene:
𝑧 1 =− (𝑎𝑏−𝑐) 𝑎 y 𝑧 2 =0.
Punto de equilibrio cero-Hopf
Un punto cero-Hopf es un punto de equilibrio de un sistema diferencial autónomo tridimensional, que tiene un valor propio cero y un par de valores propios puramente imaginarios (Llibre, 2014).
Bifurcación cero-Hopf
La bifurcación del tipo cero-Hopf es un desplie gue de dos parámetros (o familia) de un sistema di ferencial autónomo tridimensional con un equilibrio cero-Hopf. El despliegue tiene un equilibrio aislado con un valor propio cero y un par de valores propios imaginarios si los dos parámetros toman valor cero, y el despliegue tiene diferentes tipos de dinámica topológica en la pequeña vecindad de este punto de equilibrio aislado, ya que los dos parámetros varían en un pequeño entorno del origen (Llibre, 2014).
La bifurcación cero-Hopf ha sido estudiada por varios autores (Guckenheimer, 1981; Han, 1998; Guckenheimer & Holmes, 1983; Kuznetsov, 2004; Scheurle & Mardsen, 1984), y se ha demostrado que algunos conjuntos complicados invariantes del despliegue podrían ser bifurcados de los aislados equilibrios de cero-Hopf bajo algunas condiciones.
En la siguiente proposición se caracteriza cuando el punto de equilibrio localizado en el origen de las coordenadas de los sistemas Rössler es un punto de equilibrio cero-Hopf (Llibre, 2014).
Proposición 1. Hay dos familias de un parámetro de sistemas Rössler para las cuales el origen de las coordenadas es un punto de equilibrio cero-Hopf.
A saber:
Las familias a las cuales hace mención la Proposición 1 son las siguientes:
La Teoría del Promedio
La teoría del promedio es una herramienta clásica y madura para estudiar el comportamiento de la dinámica de los sistemas dinámicos diferenciales no lineales, y en particular de sus órbitas periódicas (Llibre, 2014).
Esta técnica de promediar convierte el problema de encontrar órbitas periódicas de los sistemas diferenciales, en encontrar ceros de algunas funciones adecuadas (Llibre, 2014).
Ahora se presentan los resultados básicos de la teoría del promedio que se necesita para estudiar y analizar las demostraciones de los resultados de este trabajo. Pero primeramente se dará algunas definiciones para una mejor comprensión de lo que sigue.
Definición Se supone que 𝑥=𝜙(𝑡) es una solución de la ecuación 𝑥 =𝑓(𝑥), con 𝑥∈𝐷, donde 𝐷 es un subconjunto abierto de ℝ 𝑛 y se supone existe un número positivo 𝑇 tal que 𝜙(𝑡+𝑇)=𝜙(𝑡) para todo 𝑡∈ℝ. Entonces 𝜙(𝑡) se llama solución periódica de la ecuación con periódo 𝑇, (Llibre, 2014).
Definición Una órbita periódica aislada en el conjunto de todas las órbitas periódicas de una ecuación diferencial se la conoce como un ciclo límite, (Gine, Grau & Llibre, 2013).
El siguiente teorema proporciona una aproximación de primer orden para las soluciones periódicas de un sistema diferencial periódico.
Se considera el sistema diferencial
con 𝑥∈𝐷⊂ ℝ 𝑛 , 𝐷 un dominio acotado y 𝑡≥0.
Además, se supone que 𝑓(𝑡,𝑥(𝑡)) y 𝑔(𝑡,𝑥(𝑡),𝜀) son T-periódicas en 𝑡.
La ecuación promediada asociada al sistema (2) se define como
Donde
Bajo ciertas condiciones las soluciones de equilibrio de la ecuación promediada se corresponden con las soluciones periódicas de la ecuación (2).
Teorema 1. Se considera los dos problemas de valor inicial (2) y (3). Además, se supone:
(i) 𝑓 su Jacobiano 𝜕𝑓/𝜕𝑥, su Hessiano 𝜕 2 𝑓/𝜕 𝑥 2 , 𝑔 y su Jacobiano 𝜕𝑔/𝜕𝑥 son definidos, continuos y acotados por una constante independiente 𝜀 en .
(ii) 𝑓 y 𝑔 son T-periódicas en 𝑡 (T independiente de 𝜀).
Entonces las siguientes afirmaciones son válidas:
(a) Si 𝑝 es un punto de equilibrio de la ecuación promediada (3) y
entonces existe una solución T-periódica 𝜑(𝑡,𝜀) de la ecuación (2) tal que 𝜑(𝑡,𝜀)→𝑝 cuando 𝜀→0.
(b) La estabilidad o inestabilidad del ciclo límite 𝜑(𝑡,𝜀) viene dada por la estabilidad o inestabilidad del punto de equilibrio 𝑝 del sistema promediado (3). De hecho, el punto singular 𝑝 tiene el comportamiento de estabilidad de la aplicación asociada al ciclo límite 𝜑(𝑡,𝜀).
Para la prueba del Teorema 1. se utilizan el Teorema 2 y Teorema 6 , cuyas demostraciones se pueden ver en (Verhulst, 2006) y el capítulo 11 en (Sanders, Verhulst & Murdock, 2007).
Teorema 2. Se considera la ecuación (2). Se supone que tanto 𝑓(𝑡,𝑥) como 𝑔(𝑡,𝑥,𝜀) son T-periódicas en 𝑡. Además, se supone que:
a. Las funciones vectoriales 𝑓,𝑔,𝜕𝑓/𝜕𝑥, 𝜕 2 𝑓/𝜕 𝑥 2 y 𝜕𝑔/𝜕𝑥, están definidas, son continuas y acotadas por una constante 𝑀 (independiente de 𝜀) en
b. f y g son T-periódicas en t (T independiente de 𝜀).
Si 𝑝 es un punto crítico de la ecuación promediada (3), mientras que
entonces existe una solución T-periódica 𝜑(𝑡,𝜀) de la ecuación (2) que está cerca de 𝑝 tal que
El resultado de este teorema sostiene la demostración de la afirmación del apartado (𝑎) de Teorema 1 .
Por otro lado, la demostración del apartado (𝑏) del Teorema 1 se sustenta con el Teorema 6 ; y para la demostración de este último se utiliza los siguientes teoremas; Teorema 3 (Floquet) , Teorema 4 y el Teorema 5 ; cuyas demostraciones se pueden encontrar en los capítulos 6 y 7 en (Verhulst, 2006), ver también (Sanders, Verhulst & Murdock, 2007).
Teorema 3. (Floquet) Se considera la ecuación 𝑥 =𝐴(𝑡)𝑥 con 𝐴(𝑡) una matriz de 𝑛×𝑛 continua T-periódica. Cada matriz fundamental 𝜑(𝑡) de la ecuación 𝑥 =𝐴(𝑡)𝑥 se puede escribir como el producto de dos matrices de 𝑛×𝑛, esto es: 𝜑(𝑡)=𝑃(𝑡) 𝑒 𝐵𝑡 con 𝑃(𝑡) T-periódica y 𝐵 una matriz constante 𝑛×𝑛.
Teorema 4. Se considera la ecuación 𝑥 =𝐴(𝑡)𝑥+𝑓(𝑡,𝑥) en ℝ 𝑛 , con 𝐴(𝑡) una matriz T-periódica; la función vectorial 𝑓(𝑡,𝑥) es contínua en 𝑡 y en 𝑥, y Lipschitz-continua en 𝑥 para 𝑡∈ℝ, en una vecindad de 𝑥=0. Además, se tiene:
lim ‖𝑥‖ → 0 ‖𝑓(𝑡,𝑥)‖ ‖𝑥‖ =0 uniformemente continua en 𝑡.
Si las partes reales de los exponentes característicos de la ecuación periódica lineal 𝑦 =𝐴(𝑡)𝑦 son negativos, la solución 𝑥=0 de la ecuación 𝑥 =𝐴(𝑡)𝑥+𝑓(𝑡,𝑥) es asintóticamente estable.
Teorema 5. Se considera la ecuación 𝑥 =𝐴𝑥+𝐵(𝑡)𝑥+𝑓(𝑡,𝑥) con 𝑡≥ 𝑡 0 en ℝ 𝑛 .
A es una matriz 𝑛×𝑛 constante con valores propios de los cuales al menos una tiene en la parte real valores positivos; 𝐵(𝑡) es una matriz 𝑛×𝑛 continua con la propiedad: lim 𝑡 → ∞ ∥𝐵(𝑡)∥=0.
La función vectorial 𝑓(𝑡,𝑥) es continua en 𝑡 y 𝑥, Lipschitz-continua en 𝑥 en una vecindad de 𝑥=0; si, además, se tiene que: lim ‖𝑥‖ → 0 ‖𝑓(𝑡,𝑥)‖ ‖𝑥‖ =0 uniformemente continua en 𝑡, la solución trivial de la ecuación 𝑥 =𝐴𝑥+𝐵(𝑡)𝑥+𝑓(𝑡,𝑥) con 𝑡≥ 𝑡 0 es inestable.
Teorema 6. Se considera la ecuación (2) y se supone que las condiciones del Teorema 2 se cumplen. Si los valores propios del punto crítico 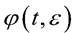 de la ecuación promediada (3) todos tienen partes reales negativas, la solución periódica correspondiente 𝜑(𝑡,𝜀) de la ecuación (2) es asintóticamente estable para 𝜀 suficientemente pequeño. Si uno de los valores propios tiene una parte real positiva, 𝜑(𝑡,𝜀) es inestable.
de la ecuación promediada (3) todos tienen partes reales negativas, la solución periódica correspondiente 𝜑(𝑡,𝜀) de la ecuación (2) es asintóticamente estable para 𝜀 suficientemente pequeño. Si uno de los valores propios tiene una parte real positiva, 𝜑(𝑡,𝜀) es inestable.
Resultados
En esta sección se presentan los resultados de aplicar la teoría del promedio al sistema diferencial Rössler, más específicamente, se menciona cuándo los sistemas Rössler tienen un equilibrio cero-Hopf, con el cual se produce alguna órbita periódica; para ello se enuncian los siguientes teoremas:
Teorema 7. Sea (𝑎,𝑏,𝑐)=( 𝑎 +𝜀𝛼,1+𝜀𝛽, 𝑎 +𝜀𝛾) con 𝑎 ∈(− 2 , 2 )\{0} y 𝜀 suficientemente pequeño. Si: 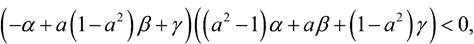 (8) y
(8) y 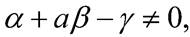 entonces el sistema Rössler (1) tiene una bifurcación del tipo cero-Hopf en el punto de equilibrio localizado en el origen de coordenadas, y una órbita periódica nace en este equilibrio cuando 𝜀=0 y existe para 𝜀>0 suficientemente pequeño. Por otro lado, la estabilidad o la inestabilidad de esta órbita periódica viene dada por los valores propios:
entonces el sistema Rössler (1) tiene una bifurcación del tipo cero-Hopf en el punto de equilibrio localizado en el origen de coordenadas, y una órbita periódica nace en este equilibrio cuando 𝜀=0 y existe para 𝜀>0 suficientemente pequeño. Por otro lado, la estabilidad o la inestabilidad de esta órbita periódica viene dada por los valores propios:
En este teorema se estudia a la primera familia de parámetros del sistema Rössler obtenida en la Proposición 1 para el cual se da puntos de equilibrio del tipo cero-Hopf, y se encuentra que el sistema cuenta con una solución periódica que comienza en el punto de equilibrio cero-Hopf ubicado en el origen de las coordenadas cuando 𝜀=0, además se analiza la estabilidad o inestabilidad de la solución obtenida (Llibre, 2014).
Teorema 8. Sea (𝑎,𝑏,𝑐)=(𝜀𝛼, 𝑏 +𝜀𝛽,𝜀𝛾) con 𝑏 ∈(−1,∞) y 𝜀 un parámetro suficientemente pequeño. Usando la teoría del promedio de primer orden no se puede encontrar órbitas periódicas que bifurquen del punto de equilibrio cero-Hopf localizado en el origen de coordenadas del sistema Rössler (1).
En este teorema se estudia a la segunda familia de parámetros del sistema Rössler obtenida en la Proposición 1 para el cual se da puntos de equilibrio del tipo cero-Hopf, y se encuentra que el sistema 𝑓 1 (𝑟,𝑤)= 𝑓 2 (𝑟,𝑤)=0 tiene una solución única (0,0) y, en consecuencia, la teoría del promedio en este caso no proporciona ninguna información sobre las posibles órbitas periódicas que puede bifurcarse del equilibrio cero-Hopf (Llibre, 2014).
Conclusión
La realización del presente trabajo ha sido, particularmente, el conocimiento adquirido sobre un tema interesante e importante al momento de estudiar el comportamiento de sistemas dinámicos diferenciales no lineales, y en particular de sus órbitas periódicas, como lo es el estudio sobre el cálculo de órbitas periódicas mediante la teoría del promedio. En ese sentido, a lo largo de la elaboración de este documento, se ha podido estudiar el sistema diferencial de ecuaciones Rössler, los puntos de equilibrio y en qué condiciones dicho sistema presenta órbitas periódicas; además de comprender cuándo se da una bifurcación del tipo cero-Hopf.
En particular se comprobó que un enfoque viable que se puede aplicar para detectar órbitas periódicas, al menos para sistemas diferenciales particulares que se someten a la bifurcación de un punto de equilibrio cero-Hopf como lo es el sistema diferencial tridimensional del tipo Rössler, es mediante la aplicación de la teoría del promedio.
Por tanto, en el desarrollo del trabajo se comprobaron las siguientes afirmaciones: el punto de equilibrio localizado en el origen de coordenadas de los sistemas Rössler, es un punto de equilibrio cero-Hopf según la caracterización dada; y de que la aplicación de la teoría del promedio es eficiente para obtener órbitas periódicas a partir de la bifurcación del tipo Hopf.
Finalmente se analizaron dos teoremas que sustentan al teorema que proporciona una aproximación de primer orden para las soluciones periódicas de un sistema diferencial periódico.
Agradecimientos
A Dios, por darme fortaleza espiritual y física para hacer frente todos los desafíos que se me fueron presentando, a mis padres, hermano y hermanas, quienes desde un principio y en todo momento me dieron su apoyo y creyeron en mi capacidad de seguir aprendiendo y al Dr. Jaume Llibre Saló de la Universidad Autónoma de Barcelona, por sus enseñanzas, sus sabias y certeras recomendaciones, fueron invaluables.
Fuente de financiamiento
Fuente de financiamiento propia











 uBio
uBio