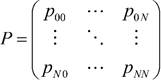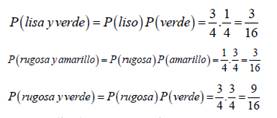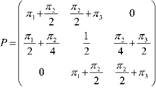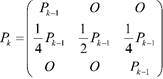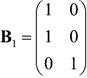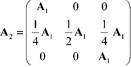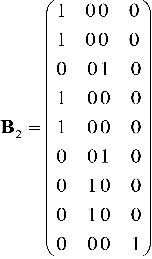Introducción
Esta investigación se ha basado en los trabajos de reseña de Forney (1973), Juang and Rabiner (1986) y Juang, B. H.(1990) y Cappé et al. (2007). Los experimentos mendelianos fueron desarrollados siguiendo los trabajos de Bilmes (1997), Thorvaldsen (2005) y Krogh et al. (1994). Las teorías necesarias para los cálculos de las probabilidades fueron tomadas de Bilmes (1997).
El comportamiento de la mayoría de los fenómenos físicos o dinámicos están gobernadas por la incertidumbre debido a la inestabilidad de las variables dentro de los procesos en el transcurso de su evolución. Esto obliga a los investigadores a desarrollar metodologías de estimación acerca del comportamiento de estos fenómenos, que les permiten conocer o al menos reducir la incertidumbre acerca de los mismos. Estas metodologías de estimación pueden consistir en la estructuración de modelos estadísticos matemáticos que permitan la descripción y comprensión del comportamiento interno de las propiedades de las variables involucradas.
Las características fundamentales en la formación de modelos estadísticos son las variables aleatorias intervinientes en el proceso estocástico en estudio y sus distribuciones de probabilidades asociadas, lo que hace necesario el conocimiento del espacio probabilístico del cual proviene. La teoría de la probabilidad es una de las teorías que ayuda a los investigadores en su afán de comprensión de la incertidumbre.
Las cadenas de Markov forman parte de los procesos estocásticos dependientes. Uno de los modelos estadísticos markovianos más utilizados en los últimos tiempos en diversas ramas de la ciencia, como ser en la Biología, constituyen las Cadenas de Márkov Ocultas o sus siglas en inglés HMM (Hiddens Markov Models). Las características generales de estos modelos constituyen sus elementos y cada uno de los tres problemas fundamentales relacionados con ellos (evaluación, descodificación y aprendizaje). Cada uno de los tres problemas en uno modelo de Markov oculto puede ser estudiado mediante la utilización de ciertos algoritmos.
Materiales y métodos
Cadenas de Markov
En la realidad existen sistemas dinámicos que van evolucionando en el transcurso del tiempo y están gobernados por ciertas condiciones que pueden estar estructuradas sobre una base determinística. Por ello, las propiedades de los procesos físicos no cambian con el paso del tiempo, o sobre una base aleatoria, en cuyo caso los procesos se rigen por leyes probabilísticas. En general, un proceso estocástico es un modelo matemático que describe el comportamiento de un sistema dinámico sometido a un fenómeno de naturaleza aleatoria que hace que el sistema evolucione según un parámetro que normalmente es el tiempo, dado por la secuencia n = 1, 2, ..., t,..., y que va cambiando probabilísticamente de un estado a otro.
Un tipo especial de proceso estocástico constituyen las cadenas de Markov, que fueron descubiertas por el matemático ruso Andrei Andreyevich Markov (1956-1922) alrededor de 1905, y que pueden aplicarse a una amplia gama de fenómenos científicos y sociales, y se cuenta con una teoría matemática extensa al respecto.
Espacio de estados y probabilidades de transición
Una cadena de Markov es un proceso estocástico a tiempo discreto dado por el conjunto { 𝑋 𝑛 : 𝑛 = 0, 1, ....}, con un espacio de estados discreto 𝑆={ 𝑆 1 , 𝑆 2 ,...}, y que satisface la propiedad de Markov. Esto es, para cualquier entero n≥0, y para cualesquiera estados 𝑥 0 ,..., 𝑥 𝑛 , 𝑥 𝑛+1 , se cumple que:
𝑝( 𝑥 𝑛+1 | 𝑥 0 ,..., 𝑥 𝑛 ) = 𝑝( 𝑥 𝑛+1 | 𝑥 𝑛 ) (1)
Si el tiempo n+1 se considera como un tiempo futuro, el tiempo 𝑛 como el presente y los tiempos 0,1,..., c−1 como el pasado, entonces la condición dada por las cadenas de Markov establece que la distribución de probabilidad del estado del proceso al tiempo futuro n+1 depende únicamente del estado del proceso al tiempo n, y no depende de los estados en los tiempos pasados 0,1,...,𝑛−1.
La probabilidad 𝑝( 𝑋 𝑛+1 = 𝑗| 𝑋 𝑛 = 𝑖) se denota por 𝑝 𝑖𝑗 (𝑛+1,𝑛), y representa la probabilidad de transición del estado i al estado j en el tiempo n+1. Son conocidas como las probabilidades de transición en un paso. Cuando los números 𝑝 𝑖𝑗 (𝑛+1,𝑛) no dependen de n se dice que la cadena es estacionaria u homogénea en el tiempo. Por simplicidad se asume tal situación de modo que las probabilidades de transición en un paso se escriben como p ij . De esta manera, dada una cadena de Markov { 𝑋 𝑛 : 𝑛 = 0,1,...} con espacio de estados S, la función p ij con 𝑖, 𝑗∈ 𝑆 es llamada función de transición de la cadena y está dada por:
𝑝 𝑖𝑗 =𝑃( 𝑋 1 = 𝑗| 𝑋 0 = 𝑖) (2)
La función de transición de la cadena cumple con las siguientes propiedades: 𝑝 𝑖𝑗 ≥0, ∀{𝑖, 𝑗}∈𝑆, esto es por definición de probabilidad y 𝑗 𝑝 𝑖𝑗 =1, para cada i.
Matriz de transición de probabilidades
Cuando el espacio de estados es finito, esto decir 𝑆={0,1,...,𝑁}, la función de probabilidad p ij de dicha cadena puede ser expresada mediante la matricial cuadrada P de la siguiente manera.
Esta matriz captura la esencia del proceso y determina el comportamiento de la cadena en cualquier tiempo futuro. La entrada (i, j) es la probabilidad de transición p ij , es decir la probabilidad de pasar del estado i al estado 𝑗 en una unidad de tiempo. El índice i se refiere al renglón de la matriz y el índice j a la columna. Esta matriz cumple las siguientes condiciones: 𝑝 𝑖𝑗 ≥0 y 𝑗=1 𝑁 𝑝 𝑖𝑗 =1. Si además satisface la condición 𝑖=1 𝑁 𝑝 𝑖𝑗 =1 dice que es una matriz doblemente estocástica.
Distribución de probabilidad inicial
En general puede considerarse que una cadena de Markov inicia su evolución partiendo de un estado 𝑖 cualquiera, o más generalmente considerando una distribución de probabilidad inicial sobre el espacio de estados.
Una distribución inicial para una cadena de Markov con espacio de estados dado por 𝑆 = {0,1,...} es simplemente una distribución de probabilidad sobre este conjunto, es decir una función 𝜋 𝑖 , que corresponde a la probabilidad de que la cadena inicie en el estado 𝑖, tal que:
𝜋 𝑖 =𝑃( 𝑋 0 =𝑖), ∀𝑖∈𝑆 (3)
Si el espacio de estados es finito, es decir 𝑆 = {0,1,2,...,𝑁}, entonces la distribución inicial podría verse como una n-tupla aleatoria 𝛱 = ( 𝜋 0 ,..., 𝜋 𝑁 ).
Caracterización de la propiedad markoviana en un proceso estocástico
En todo proceso estocástico que cumpla con la propiedad de Markov es posible calcular la distribución conjunta de cualquier secuencia finita de variables aleatorias en el proceso. Esto es, si 𝑋 0 , 𝑋 1 ,..., 𝑋 𝑛 constituye una secuencia de variables aleatorias se tiene que:
𝑝( 𝑥 0 𝑥 1 ,..., 𝑥 𝑛 ) = 𝜋 0 𝑖=1 𝑛 𝑝( 𝑥 𝑖 | 𝑥 𝑖−1 ) (4)
Dígrafos de transición
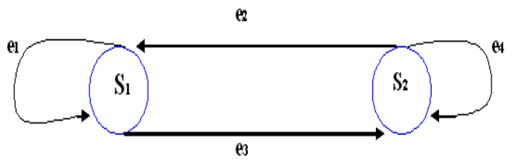
Un dígrafo o grafo dirigido es una tripleta (S, E, I) , donde S es un conjunto cuyos elementos son llamados vértices, E otro conjunto cuyos elementos son las aristas y finalmente I es una función que le asocia a cada arista 𝑒∈𝐸 un par ordenado de vértices llamados extremo de 𝑒. El primer vértice es llamado la cola y el segundo la cabeza de 𝑒. Generalmente un dígrafo es dibujado en forma tal que cada vértice queda representado por un punto en el plano, y cada arista por una curva que une los representantes de sus extremos. Para distinguir cabeza de cola, dibujamos una flecha en la cabeza de la arista. (Figura. 1)
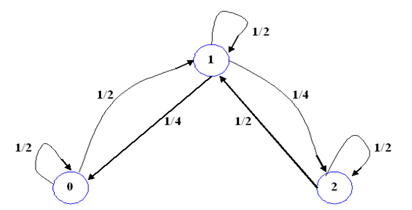
Las cadenas de Markov pueden ser representadas mediante gráficos denominados dígrafos de transición o grafos dirigidos, tal como lo muestra la Figura 2. Estas cadenas suelen ser analizadas mediante la utilización de grafos dirigidos con pesos, que están constituidos por una terna (S, E, I), donde los elementos de S (conjunto de nodos) son los estados de la cadena de Markov. Los elementos del conjunto E (conjunto de aristas) constituyen arcos, simbolizados 𝑒=(𝑖, 𝑗), a los cuales son asignadas probabilidades no nulas de transición, 𝑝 𝑖𝑗 >0. Las aristas pueden también presentarse como bucles o lazos, situaciones en las cuales los arcos empiezan y terminan en un mismo nodo.
Evolución de las cadenas de Markov
Una cadena de Markov con espacio de estados finito 𝑆={0,1,...,𝑁} y distribución inicial 𝛱=( 𝜋 0 ,..., 𝜋 𝑁 ) puede dividirse en sectores sobre el espacio de estados de acuerdo a un criterio fácilmente observable; pero esta división en subconjuntos no es estable ya que va evolucionando en el tiempo y el proceso queda establecido en 𝑁 sectores o estados del proceso y en un instante dado la condición de la situación es 𝑉 𝑘 =( 𝑣 𝑘 (0), 𝑣 𝑘 (1) ,..., 𝑣 𝑘 (𝑁)),∀𝑘 ∈ {0,1,...}, donde cada 𝑣 𝑘 (𝑖), ∀𝑖∈{0,1,...,𝑁}, indica el tamaño del sector 𝑖-ésimo en el instante 𝑘, ya sea en magnitud absoluta, en porcentaje del total, o en porción de unidad.
Al utilizar porciones de la unidad para representar las componentes 𝑣 𝑘 (𝑖) de 𝑉 𝑘 , se tendrá que cada 𝑉 𝑘 es una distribución de probabilidad, sus componentes son no negativas y suman 1. Como la observación no se realiza en todo momento, sino al término de lapsos iguales de tiempos, se tendrá que 𝑉 𝑘 depende del período en que se realiza la observación durante el proceso, es decir es una función de variable que va tomando valores en los números naturales 0, 1, …… y arroja una sucesión de distribuciones Π, 𝑉 1 , 𝑉 2 , … , 𝑉 𝑘 , 𝑉 𝑘+1 , … donde 𝛱 indica cómo es cada sector en el inicio del proceso y se supone que la distribución 𝑉 𝑘 depende linealmente de la distribución anterior 𝑉 𝑘−1 , es decir existe una matriz de probabilidades de transición 𝑃 de orden de (n x n) tal que:
𝑉 𝑘 = 𝑉 𝑘−1 . 𝑃= 𝛱 . 𝑃 (𝑘) (5)
Con todo lo expresado, se puede concluir que cualquier secuencia observada en una cadena de Markov queda totalmente especificada por la distribución inicial y la matriz de probabilidades de transición.
Probabilidades de transición en 𝐧 pasos
En una cadena de Markov { 𝑋 𝑛 : 𝑛 = 0,1,...}, con espacio de estados 𝑆 y función de transición dada por 𝑝 𝑖𝑗 =𝑃( 𝑋 1 = 𝑗| 𝑋 0 = 𝑖), 𝑃( 𝑋 𝑚+𝑛 = 𝑗| 𝑋 𝑚 = 𝑖) corresponde a la probabilidad de pasar del estado 𝑖, en el tiempo 𝑚, al estado 𝑗, en el tiempo m+n. Dado el supuesto de la condición de homogeneidad en el tiempo, esta probabilidad no depende realmente del tiempo 𝑚, por lo que coincide con la probabilidad 𝑃( 𝑋 𝑛 = 𝑗| 𝑋 0 = 𝑖), y se denota por 𝑝 𝑖𝑗 (𝑛) o 𝑝 𝑖𝑗 (𝑛) , donde el número de pasos n se escribe entre paréntesis para distinguirlo de algún posible exponente, y se llama probabilidad de transición en n pasos.
Si el espacio de estados es finito, las probabilidades de transición pueden ser expresadas mediante la matriz de transición de probabilidades P y por lo tanto, la función de transición en n pasos es igual a la potencia n-ésima de la matriz P.
Comunicación
Para que dos estados en una cadena de Markov se comuniquen necesariamente debe darse la propiedad de accesibilidad entre ellos. De esta forma, un estado 𝑗 es accesible desde un estado 𝑖 cuando se tenga un entero n≥0 tal que 𝑝 𝑖𝑗 (𝑛) ≥0. Por lo tanto, los estados 𝑖 y 𝑗 se comunican si 𝑖 es accesible desde el estado j y j es accesible desde el estado i. La comunicación entre dos estados constituye la posibilidad de pasar de un estado a otro en un número finito de transiciones e indica una partición del espacio de estados de la cadena dada por los subconjuntos de estados comunicantes. Esto es, dos estados pertenecen al mismo elemento de la partición si y solo si, tales estados se comunican. De este modo el espacio de estados de una cadena de Markov se subdivide en clases de comunicación.
Como la propiedad de accesibilidad constituye una relación de equivalencia, se cumple que: todo estado 𝑖 es accesible desde si mismo, si el estado 𝑖 es accesible desde el estado 𝑗 se tiene que el estado 𝑗 es accesible desde el estado i y si el estado i es accesible desde el estado j y el estado j es accesible desde el estado k entonces el estado i es accesible desde el estado k.
Estados absorbentes, recurrentes y transitorios
En una cadena de Markov, un estado 𝑖 es absorbente si 𝑝 𝑖𝑖 =1. Mientras que un estado 𝑖 es recurrente si la probabilidad de eventualmente regresar a i, partiendo de i, es uno, es decir si:
𝑃( 𝑋 𝑛 = 𝑖 𝑝𝑎𝑟𝑎 𝑎𝑙𝑔𝑢𝑛𝑎 𝑛 ≥ 1| 𝑋 0 = 𝑖) = 1 (6)
Todo estado absorbente es un estado recurrente. Un estado que no sea recurrente recibe el nombre de transitorio, y en tal caso la probabilidad anterior es menor a uno.
Estados límites y de equilibrio
Dada una cadena de Markov cuya matriz de probabilidades de transición es P, sea 𝑉 una distribución de probabilidad. Diremos que V es la distribución de equilibrio del proceso, si se verifica que
Si un proceso llegara a una distribución de equilibrio, se haría constante, es decir, todas las distribuciones posteriores serían iguales.
Por otra parte, sea { 𝑋 𝑛 : 𝑛 = 0,1,...} una cadena de Markov con espacio de estado finito que tiene una distribución inicial 𝛱 y matriz de transición P. De acuerdo a la noción de convergencia, cabe preguntarse si existe:
𝑉 ∞ = lim 𝑘→∞ 𝑉 𝑘 =𝛱 lim 𝑘→∞ 𝑃 (𝑘) = 𝛱 𝑃 (∞) (8)
En caso de existir, se dice que 𝑉 ∞ es la distribución límite o de equilibrio de la cadena de Markov.
Regularidad
Las cadenas de Markov regulares son cadenas finitas que cumplen con la propiedad Markoviana y que a partir de un cierto momento un vector de estado pasa a otro cualquiera con probabilidades estrictamente positivas en un paso. Esto es, una cadena de Markov finita tiene matriz de transición regular si existe un entero no negativo, n≥0, tal que 𝑝 𝑖𝑗 𝑛 >0, para cualesquiera estados i y j. Entonces, una cadena de Markov será regular si alguna potencia de su matriz de probabilidades de transición tiene todas sus entradas estrictamente positivas.
Cadenas de Markov ocultas
La idea general de un Modelo Oculto de Markov (HMM) también llamada cadena de Markov oculta está en el hecho de que, al medir o cuantificar cierto fenómeno, la lectura que genera la secuencia observable de símbolos no necesariamente es el proceso real del fenómeno, ya que el instrumento de medición podría estar introduciendo un ruido en la verdadera señal. Por esta razón, este tipo de modelamiento introduce dos procesos: uno observable y otro oculto. En este modelo el proceso oculto es una cadena de Markov homogénea con espacio de estados finito y no se requiere que el proceso observado cumpla con la propiedad de Markov, sino que sea simplemente un proceso estocástico.
Los modelos ocultos de Markov (HMM) fueron introducidos a finales de los sesenta y principios de los setenta por Leonard E. Baum en un artículo, el cual propuso este modelo como un método estadístico de estimación de las funciones probabilísticas de las cadenas de Markov.
Desde finales de 1970 cuando los modelos ocultos de Markov fueron aplicados a sistemas de reconocimiento de voz, se desarrollaron técnicas para estimar probabilidades sobre estos sistemas en específico. Estas técnicas permiten a estos modelos llegar a ser eficientes, robustos y flexibles de manera computacional.
Un modelo oculto de Markov constituye una técnica de modelización de datos secuenciales aplicada inicialmente en el campo del reconocimiento automático del habla (Rabiner,1989), donde actualmente es una herramienta casi imprescindible. Este modelo puede ser pensado como una máquina de estados finito donde las transiciones entre los estados dependen de la ocurrencia de algún símbolo. En general, son muy útiles para el reconocimiento de patrones y en particular son substancialmente efectivos para modelar el comportamiento del hombre o procesos en los que existe la intervención del hombre.
Formalmente, una cadena de Markov oculta es un proceso binario (doblemente estocástico) { 𝑋 𝑛 , 𝑌 𝑛 }, ∀𝑛 ∈ {0,1,2,...}, donde { 𝑋 𝑛 } es una cadena de Markov homogénea con espacio de estados finito y { 𝑌 𝑛 } es un proceso estocástico cuya distribución condicional solo depende de { 𝑋 𝑛 }.
Se entiende entonces que los modelos ocultos de Markov son modelos estadísticos que juntan de acuerdo a leyes probabilísticas una colección de variables aleatorias { 𝑌 1 , 𝑌 2 ,... 𝑌 𝑇 , , 𝑋 1 𝑋 2 ,,..., 𝑋 𝑇 }, con 𝑇 finito. Las variables 𝑌 𝑡 pueden ser observaciones continuas o discretas y las variables 𝑋 𝑡 son variables ocultas y discretas. Los HMM pueden particularizarse de acuerdo a las leyes probabilísticas que gobiernan a las variables aleatorias que intervienen en el modelo. En este tipo de modelos probabilísticos se asumen dos condiciones de independencia que son:
la 𝑡-ésima variable aleatoria: dada la (t -1)-ésima variable aleatoria del proceso oculto, es independiente de variables previas, es decir que X t depende solamente de la Xt-1 con lo que:
𝑃( 𝑋 𝑡 | 𝑋 𝑡−1 , 𝑌 𝑡−1 ,..., 𝑋 1 , 𝑌 1 ) = 𝑃( 𝑋 𝑡 | 𝑋 𝑡−1 ) (9)
la 𝑡-ésima observación: dada la 𝑡-ésima variable oculta, es independiente de cualquier otra variable, es decir que Y t depende solo de X t , con lo que
𝑃 𝑌 𝑡 𝑋 𝑇 , 𝑌 𝑇 ,..., 𝑋 𝑡+1 , 𝑌 𝑡+1 , , 𝑋 𝑡 , 𝑌 𝑡 , , 𝑋 𝑡−1 , 𝑌 𝑡−1 ,..., 𝑋 1 , 𝑌 1 )=𝑃( 𝑌 𝑡 | 𝑋 𝑡 ) (10)
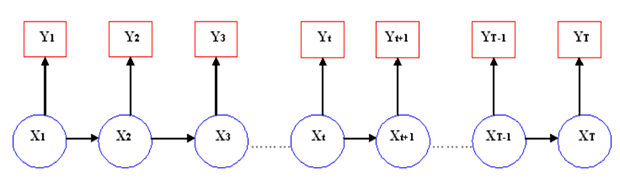
La Figura 3 es un modelo probabilístico gráfico que muestra un conjunto de variables aleatorias y sus condiciones de dependencia. Esta gráfica es llamada Red Bayesiana dinámica simple y refleja las dos condiciones de independencia impuestas a las variables aleatorias intervinientes en los HMM. Los círculos en azul representan a las variables aleatorias del proceso oculto y los rectángulos en rojo a las del proceso visible. Estas variables aleatorias pueden tomar ciertos valores en cada instante t, además cada símbolo X t representa una variable aleatoria del proceso markoviano discreto oculto en el instante t, mientras que los símbolos Y t constituyen las variables aleatorias del proceso observable en cada instante t. Las flechas indican las formas de dependencias condicionales entre las variables aleatorias.
Elementos de los HMM discreto
Si se tiene que las observaciones 𝑌 𝑡 son discretas con N posibles valores, entonces estamos ante una cadena de Markov oculta discreta. En los HMM discretos intervienen los siguientes elementos:
𝑆={1,2,...,𝑁} es el conjunto finito de estados del proceso oculto, en donde 𝑁 es la cantidad total de estados en el modelo. 𝑉 es el conjunto de valores o símbolos diferentes que se pueden observar en cada uno de los estados, puede considerarse también un alfabeto finito. Cada uno de los símbolos que un estado puede emitir se denota como { 𝑣 1 , 𝑣 2 ,..., 𝑣 𝑀 }, donde 𝑀 es el número de símbolos del alfabeto y cada 𝑣 𝑘 se refiere a un símbolo diferente.
𝜫=( 𝜋 1 , 𝜋 2 ,..., 𝜋 𝑁 ) es la distribución de probabilidad inicial de los estados del proceso oculto, con 𝜋 𝑖 = 𝑃( 𝑋 1 = 𝑖), ∀𝑖 ∈ {1,2,...,𝑁} y 𝐼=1 𝑁 𝜋 𝑖 =1. Cada 𝜋 𝑖 representa la probabilidad de que el proceso esté en el estado 𝑖 en el instante en que se inicia.
𝐀={ 𝑝 𝑖𝑗 } constituye la matriz de probabilidades de las transiciones entre los estados del proceso estocástico oculto, es decir: 𝑝 𝑖𝑗 =𝑃( 𝑋 𝑛+1 =𝑗| 𝑋 𝑛 = 𝑖), ∀{𝑖, 𝑗}∈{1,2,...,𝑁} y ∀𝑛 ∈ {1,2,...}. Por lo cual, cada 𝑝 𝑖𝑗 constituye la probabilidad de que el sistema se encuentre en el estado j en el tiempo n+1 dado que se encuentra en el estado 𝑖 en el tiempo n.
𝐁={ 𝑏 𝑖 (𝑘)} constituye la matriz de probabilidad de emisión de un estado dado. Constituye la distribución de probabilidad de los estados en el proceso observable, en donde cada 𝑏 𝑖 (𝑘)=𝑃( 𝑌 𝑛 = 𝑣 𝑘 | 𝑋 𝑛 =𝑖), ∀𝑖∈{1,2,...,𝑁}, ∀𝑛∈{1,2,…} y ∀𝑘 ∈ {1,2,...,𝑀} con 𝐼=1 𝑁 𝑏 𝑖 (𝑘) =1. Cada 𝑏 𝑖 (𝑘) constituye la probabilidad de que el sistema, estando en el instante n en el estado i, genere la observación 𝑣 𝑘 .
Cualquier secuencia de observaciones generadas dentro del proceso se simboliza por 𝑌 = ( 𝑌 1 , 𝑌 2 ,..., 𝑌 𝑘 ), donde cada 𝑌 𝑖 ∈𝑉, ∀𝑖 ∈ {1,2,..., 𝑘}, representa una observación y K es la cantidad de observaciones en la secuencia.
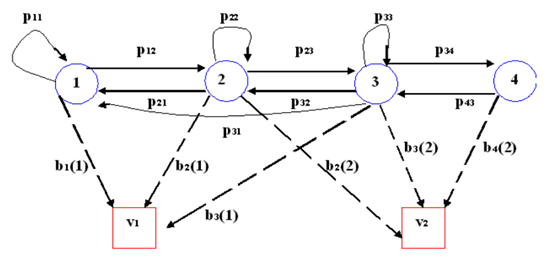
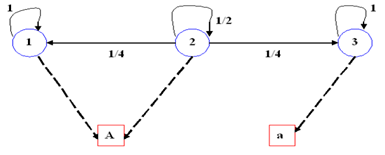
La Figura 4 muestra el modelo gráfico de un HMM con cuatro estados ocultos y dos tipos de observaciones. Las flechas continuas indican las transiciones entre los estados del proceso markoviano oculto ( 𝑝 𝑖𝑗 >0), y las flechas punteadas constituyen las probabilidades de emisión de observación en cada estado oculto ( 𝑏 𝑖 𝑘 >0).
Experimentos mendelianos
En 1866, se publicaron los famosos experimentos de Mendel en la hibridación de las plantas, el cual es considerado a menudo el trabajo de rompimiento del hielo de la genética moderna. Mendel no tenía ningún conocimiento anterior de la naturaleza dual de los genes, pero a través de una serie de experimentos en el jardín de su convento, pudo detectar la presencia de gen oculto y nombrarlo “Elemente”.
El mundo biológico es bastante complejo y a menudo demasiado complicado para el modelado matemático. En comparación con la física, solo recientemente han atacado problemas biológicos mediante el uso de métodos matemáticos enfocados a lo computacional. La más nueva y más desafiante interacción entre la biología y la matemática viene de la biología molecular moderna y de la bioinformática.
La genética ha tenido una explosión en número de descubrimientos y se ha desarrollado a la par del avance computacional. Experimentos como los de Gregor Mendel (1822-1884), titulado “los experimentos en los híbridos de las plantas (1866)”, pueden ser revisitados y las leyes de la herencia redescubiertas usando las técnicas y los datos de su publicación original. La genética mendeliana se refiere a la transmisión de los rasgos biológicos discretos de una generación a otra y los modos de expresión de los genes.
Los inicios, las cuentas y los experimentos realizados por Mendel
Mendel fue miembro del monasterio de Santo Tomás en Brünn, República Checa, a la edad de 21 años y estudió teología entre los años 1844 y 1848. Fue profesor de ciencias, física y matemática. Estudió en la Universidad de Viena entre 1851 y 1853. Su maestro más influyente fue Andreas Von Ettingshausen. Escribió un libro en combinatoria ("Die combinatorische Análisis", Viena, 1826), y había recogido claramente algunos de los métodos utilizados allí, más tarde en su serie de experimentos con las plantas. Resultó ser un buen experimentador en el jardín del monasterio, a pesar de que sólo tenía acceso a equipos bastantes simples. Hizo sus clásicos experimentos en la cría de plantas entre los años 1856 y 1863, donde cultivó y experimentó con al menos 28.000 plantas.
Los guisantes son la cuarta parte más importante en el cultivo de legumbres del mundo. Mendel eligió un guisante común del jardín que eran arvejas de la especie Pisum sativum para sus primeros experimentos en la hibridación por motivos prácticos (eran baratos, fáciles de obtener y tienen un tiempo de generación relativamente corto) y por otras dos razones que fueron cruciales para el éxito de sus experimentos, ya que las semillas de las arvejas presentaban variedades de formas y colores fáciles de identificar y analizar. Además, estas plantas, en forma silvestre se autofecundan y pueden ser manipuladas por el experimentador de modo tal que se puede dirigir la reproducción entre dos individuos (fecundación cruzada).
Las arvejas son plantas que se autofecundan de manera natural y exhiben caracteres que se presentan de manera simple y en distintas formas. Un carácter es un cierto rasgo o característica específica de un organismo y en general posee diferentes variantes, formas en que puede presentarse. Para lograr arvejas con ciertos caracteres, Mendel las cultivó durante muchas generaciones obteniendo líneas puras, es decir, subpoblaciones que producían descendencia homogénea para cada carácter elegido. Obtuvo siete parejas de líneas puras para siete caracteres, diferenciando cada pareja sólo respecto de un carácter. Los siete caracteres, junto con sus respectivas variantes, estudiados por Mendel en las arvejas se presentan en la Tabla 1.
Tabla 1 Caracteres versus variantes en las arvejas
| Carácter | Variante | |
|---|---|---|
| Color de la flor | Rojo | Blanco |
| Color de la semilla | Amarillo | Verde |
| Textura de la semilla | Lisa | Rugosa |
| Forma de la vaina | Hinchada | Hendida |
| Color de la vaina | Verde | Amarillo |
| Longitud del tallo | Largo | Corto |
| Tipo de floración | Terminal | Axial |
Color de las flores de las plantas
El primer carácter estudiado por Mendel fue el color de las flores de las plantas. Como primer paso fecundó una planta de flores rojas con el polen de una planta de flores blancas, estos ejemplares de líneas puras constituyen la generación parental (P). Este cruzamiento originó la primera generación filial (F1), cuyos integrantes tenían todos flores rojas. Luego tomó plantas de flores blancas y las fecundó con polen de plantas de flores rojas y obtuvo los mismos resultados.
En su segundo experimento, tomó los ejemplares de la primera generación filial (F1) y las autofecundó, obteniendo como resultado 929 semillas en la segunda generación filial (F2), que luego sembró y cuando comenzaron a dar flores, se observó que algunas plantas tenían flores blancas, con lo cual había reaparecido la otra variante. Con estos resultados, primero contó la cantidad de individuos de cada variante hallada en F2 y calculó la proporción entre ellos, encontró que de un total de 929 plantas de F2, 705 tenían flores rojas y 224 tenían flores blancas. Las proporciones eran de aproximadamente 3:1, de cada 4 flores 3 eran de color rojo.
Mendel dedujo que F1 recibe la capacidad de producir flores rojas o blancas. Sin embargo, una de las variantes (flor blanca) no se expresa. Para denominar este fenómeno, utilizó el término dominante para designar a la variante que se expresa en F1 y el término recesivo, para la variante que queda enmascarada y reaparece en F2.
Color de las semillas
Siguiendo con sus experimentos, Mendel estudió el color de las semillas. La ventaja de usar este carácter era que no tenía que esperar a que cada uno de los individuos de cada generación floreciera. Para este carácter, dedujo que el color amarillo es dominante y que el color verde era recesivo. Además, pensó que, si a partir de las plantas con semillas amarillas de F1 surgieron, en F2, plantas con semillas verdes, era posible que, a su vez, las plantas amarillas de F2 también “escondieran” el carácter verde.
Para analizar su idea, Mendel autofecundó 519 plantas con semillas amarillas de F2 y vio que 166 de ellas sólo producían arvejas con semillas amarillas. Las llamó “amarillas puras”. Por otra parte, 353 plantas producían arvejas con semillas amarillas y verdes, nuevamente en una proporción 3:1. De cada cuatro semillas tres eran de color amarillo, llamadas “amarillas impuras”. Por lo tanto, de las plantas con semillas amarillas en F2, alrededor de los 1/3 eran como el parental amarillo de línea pura y los 2/3 eran como los amarillos de F1, es decir, producían semillas amarillas y verdes en una proporción 3:1.
Por otra parte, las plantas con semillas verdes siempre daban arvejas con semillas verdes, por lo que eran puras siempre. Con estos resultados, Mendel se dio cuenta que era preciso distinguir la constitución genética de un individuo, su genotipo, de la expresión visible del mismo, su fenotipo.
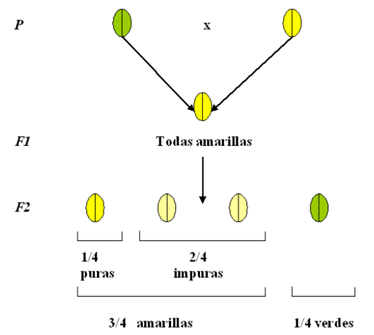
Entonces, en F1 se tiene al fenotipo amarillo y en F2 a los fenotipos amarillo y verde. Las plantas con fenotipos amarillos en F2 no son todas iguales. Utilizando la notación 𝐴, para la variante dominante (amarilla) y 𝑎 para la variante recesiva (verde), podemos representar a los genotipos de F2 de la siguiente manera: el genotipo 𝐴𝐴 corresponde a las plantas con semillas “amarillas puras”, el genotipo 𝑎𝐴 corresponde a las plantas con semillas “amarillas impuras” y el genotipo 𝑎𝑎 corresponde a las plantas con semillas “verdes” (Figura 5).
Según los resultados, en F2 se contemplan dos tipos de fenotipos, amarillo y verde, pero tres tipos de genotipos, denominadas homocigota dominante (AA), heterocigota (Aa) y homocigota recesiva (aa). En su documento, Mendel informó que realizó sus experimentos para cuatro a seis generaciones, sin dar más cifras, indicando solamente los resultados generales y fórmulas matemáticas.
Textura y color de las semillas
A fin de responder a la pregunta: ¿cómo serían las proporciones cuando se consideran dos caracteres simultáneamente? Mendel consideró en su siguiente experimento los caracteres “textura de la semilla”, cuyas categorías son lisa (B) y rugosa (b), y “color de las semillas” con categorías amarillo (A) y verde (a), utilisando dos líneas puras: plantas con semillas lisas y verdes cuyos genotipos son de la forma aaBB y plantas con semillas rugosas y amarillas con genotipos AAbb.
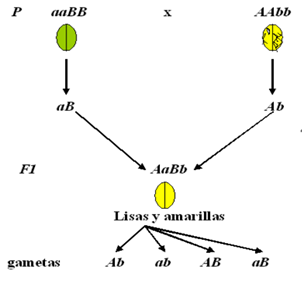
Figura 6: Resultados obtenidos en la primera generación filial (F1) al tomar los caracteres textura y color de las semillas simultáneamente
En el cruzamiento de las dos líneas puras (AAbb x aaBB), tal como lo muestra la Figura 6, se observó que en F1 todas las semillas eran lisas y amarillas con genotipos AaBb, es decir que es homogénea y su fenotipo es el correspondiente a la forma dominante de cada carácter, en este caso liso y amarillo. En F2, Mendel obtuvo las cuatro combinaciones fenotípicas posibles (liso y amarillo, liso y verde, rugoso y amarillo, y rugoso y verde) en proporción 9:3:3:1, tal como lo muestra la Tabla 2.
Tabla 2 Resultados obtenidos en la segunda generación filial (F2) al tomar los caracteres textura y color de las semillas simultáneamente
| Cantidades | Proporciones |
|---|---|
| 315 semillas lisas y amarillas | 9 |
| 108 semillas lisas y verdes | 3 |
| 101 semillas rugosas y amarillas | 3 |
| 32 semillas rugosas y verdes | 1 |
| 556 semillas en total | 16 |
Analizando primeramente el carácter textura de la semilla, que está compuesta de 423 semillas lisas y 133 semillas rugosas, se puede aprecia que guardan entre sí una relación 3:1. De la misma manera analizando el carácter color de las semillas se observa que 416 semillas son amarillas y 140 verdes, también guardan entre sí una relación 3:1.
Entonces, al considerarse los dos caracteres simultáneamente, los diferentes fenotipos resultantes deberían guardar entre sí una combinación de las proporciones de cada carácter por separado. Al considerar el carácter textura de la semilla, se tiene que: lisa tiene una probabilidad 3/4 y rugosa 1/4. De la misma manera, en el carácter color de las semillas, amarillo tiene una probabilidad de 3/4 y verde 1/4. Como los genes para distintos caracteres se heredan de forma independiente, se tiene:
Extendiendo este razonamiento a 𝑛 caracteres calculando las probabilidades combinadas de cada caso.
Tabla 3 Genotipos de la F2 de un cruzamiento AaBb x AaBb
| Gametas | AB | Ab | aB | ab |
| AB | AABB | AABb | AaBB | AaBb |
| Ab | AABb | AAbb | AaBb | Aabb |
| aB | AaBB | AaBb | aaBB | aaBb |
| ab | AaBb | Aabb | aaBb | aabb |
Leyes de Mendel
Las leyes de Mendel son un conjunto de reglas básicas sobre la transmisión por herencia de las características de los organismos de los padres a sus hijos.
Primera ley de Mendel: Ley de la uniformidad de los híbridos de la primera generación filial (F1).
Si se cruza una línea pura de arvejas cuya semilla es de color amarilla con otra cuya semilla es de color verde, los individuos de la primera generación filial (F1) son todos uniformes. En este caso se parece a uno de los progenitores, el de la semilla con color amarilla.
Segunda ley de Mendel: Ley de la segregación
Los dos factores (genes) para cada carácter no se mezclan ni se fusionan de ninguna manera, sino que se segregan (separan) en el momento de la formación de los gametos.
Tercera ley de Mendel: Ley de la transmisión independiente
Los genes para distintos caracteres se heredan de forma independiente
RESULTADOS Y DISCUSIÓN
Experimentos mendelianos como cadenas de Markov
Los experimentos genéticos mendelianos sobre la base de la libre fertilización, pueden representarse mediante simples modelos de Markov.
Diploide con un solo par de genes
Mendel en sus primeros experimentos estudió el color de las plantas y luego el color de las semillas de las plantas. En ambos casos tomó un solo carácter, las cuales tienen dos tipos de variantes (genes).
Considerando uno de los dos primeros experimentos mendelianos, por ejemplo, el experimento realizado sobre el carácter “color de las semillas”, en la cual las variantes (genes) son “amarillo” al que se le llamó gen dominante (A) y “verde” al que denominó gen recesivo (a). Recordando que en cada generación se pudo notar que era preciso distinguir la constitución genética de un individuo de la expresión visible del mismo (aspecto), es decir su genotipo (homocigota dominante (AA), heterocigota (aA) ó homocigota recesivo (aa)) de su fenotipo (amarillo (A) ó verde (a)). Entonces, el genotipo de las semillas puede ser de un nivel sobre el conjunto de estados posibles 𝑆={𝐴𝐴 (𝑒𝑠𝑡𝑎𝑑𝑜 1), 𝑎𝐴 (𝑒𝑠𝑡𝑎𝑑𝑜 2), 𝑎𝑎 (𝑒𝑠𝑡𝑎𝑑𝑜 3)} en el tiempo 𝑡, con probabilidades de 𝑣 𝑡 (1), 𝑣 𝑡 (2) y 𝑣 𝑡 (3), donde 𝑣 𝑡 (1)+ 𝑣 𝑡 (2)+ 𝑣 𝑡 (3)=1.
Si 𝑋 𝑡 es la variable aleatoria que muestra el estado en la que se encuentra el genotipo del individuo en el tiempo 𝑡, la distribución de probabilidad de los estados del proceso cuando evolucione en el tiempo será 𝑉 𝑡 =( 𝑣 𝑡 1 , 𝑣 𝑡 2 , 𝑣 𝑡 3 ), donde 𝑣 𝑡 (𝑖)=𝑃( 𝑋 𝑡 = 𝑖), ∀ 𝑡∈{1,2,3,...} y ∀ 𝑖∈{1,2,3}. Como al principio de su experimento Mendel tomó semillas de colores amarillas y las fecundó con semillas de colores verdes, comenzó este proceso tomando una población fundada en las primeras plantas de heterocigotas y con ello, la distribución de probabilidad inicial viene dada por 𝜫 𝟏 =(0,1,0).
Por otra parte, Mendel observó que si tomaba una población de plantas con semillas de colores amarillas puras (homocigotas dominantes) y las autofecundaba obtenía siempre plantas con semillas de colores amarillas. De manera análoga, si tomaba una población de plantas con semillas verdes puras obtenía siempre plantas con semillas de colores verdes. Ahora bien, si tomaba una población de plantas heterocigotas la relación de los genotipos era de 1:2:1, con la cual las proporciones genotípicas eran de 1/4, 1/2 y 1/4. (Figura 7)
Considerando que la segregación cromosómica (distribución de los cromosomas) es al azar y que el tiempo de transición es homogéneo, se puede definir a la matriz de transición de probabilidades de la cadena de Markov para la autofertilización como:
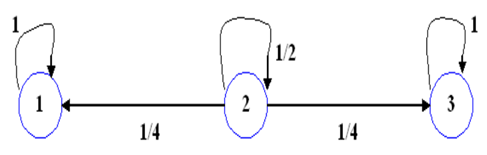
Las 𝑝 𝑖𝑗 , ∀ 𝑖,𝑗∈{1,2,3}, de la matriz de transición de probabilidades de un paso corresponden a la probabilidad de que cada célula realice la transición de un cierto estado 𝑖 a un cierto estado 𝑗. Es decir, la probabilidad del paso de un cierto genotipo a otro genotipo de un tiempo 𝑡 a otro tiempo t+1. En este proceso de Markov, el estado 2 es transitorio y los estados 1 y 3 son absorbentes. Tomando en cuenta la ecuación (5), la distribución de probabilidad de la variable aleatoria X t+1 (de los estados) en el tiempo t+1 es:
𝑉 𝑡+1 = 𝛱 1 . 𝑃 (𝑡) = 1 2 − 1 2 𝑡+1 , 1 2 ?? , 1 2 − 1 2 𝑡+1 11)
Calculando el límite de 𝑉 𝑡+1 cuando 𝑡 tiende al infinito, se obtiene:
𝑉 ∞ = lim 𝑘→∞ 𝑉 𝑘 = 1 2 , 0, 1 2 (12)
Resultado que muestra que el proceso será absorbido rápidamente por alguno de los dos estados absorbentes intervinientes en la cadena. Entonces, con la auto fertilización, una población se divide en una serie de líneas que rápidamente se vuelven muy homocigótica y que asintóticamente produce la autofecundación de dos genotipos puros, lo que hace que todos los descendientes sean del mismo tipo.
Debido a que en la reproducción incluye tanto la reproducción celular (de una célula madre se obtienen dos células hijas) como la procreación (a partir de dos células de los individuos progenitores, se produce un individuo hijo), se toma un modelo con la fertilización al azar en una población infinita diploide sin superposición entre las generaciones en lugar de la reproducción de individuos del mismo linaje (endogamia), es decir que al mezclarse dos individuos de sexos opuestos (progenitores) de la población en cada paso dan origen a un nuevo ser vivo (hijo) y este nuevo ser vivo hereda un gen de manera aleatoria de cada uno de sus progenitores. El genotipo del hijo es nuevamente de un nivel sobre el espacio de estados 𝑆 = {𝐴𝐴 (𝑒𝑠𝑡𝑎𝑑𝑜 1), 𝑎𝐴 (𝑒𝑠𝑡𝑎𝑑𝑜 2), 𝑎𝑎 (𝑒𝑠𝑡𝑎𝑑𝑜 3)}.
Al concentrarse en uno de los progenitores, por decir el padre, la distribución de probabilidad inicial está dada por 𝜫 𝟏 = ( 𝜋 1 , 𝜋 2 , 𝜋 3 ), donde 𝜋 𝑖 = 𝑃 𝑋 0 = 𝑖 = 𝑞 𝑖 indica la probabilidad de que el individuo padre escoja una madre que tenga como par de genes los correspondientes al estado 𝑖, con 𝑖∈{1,2,3}. Por otra parte, la probabilidad de que la madre tenga algún gen dominante o recesivo en el estado 𝑖 está dada por 𝑞 𝐷𝑖 o 𝑞 𝑅𝑖 . En este modelo, los elementos intervinientes en los cálculos para la obtención de las probabilidades de transición de un paso tienen las siguientes interpretaciones:
a) Si el padre tiene ambos genes dominantes y escoge a una madre para cruzarse, la probabilidad de que el hijo tenga:
ambos genes dominantes (AA que se puede simbolizar por D) es:
𝑃 𝐷 𝑡+1 𝐷 𝑡 = 𝑝 11 = 𝑞 1 𝑞 𝐷1 𝑝 𝐷 + 𝑞 2 𝑞 𝐷2 𝑝 𝐷 + 𝑞 3 𝑞 𝐷3 𝑝 𝐷
𝑝 11 = 𝜋 1 · 1 · 1+ 𝜋 2 · 1 2 · 1+ 𝜋 3 · 0 · 1 = 𝜋 1 + ?? 2 2
un gen dominante y otro recesivo (𝑎𝐴 que se puede simbolizar por 𝐻) es:
𝑃 𝐻 𝑡+1 𝐷 𝑡 = 𝑝 12 = 𝑞 1 𝑞 𝑅1 𝑝 𝐷 + 𝑞 2 𝑞 𝑅2 𝑝 𝐷 + 𝑞 3 𝑞 𝑅3 𝑝 𝐷
𝑝 12 = 𝜋 1 · 0 · 1+ 𝜋 2 · 1 2 · 1+ 𝜋 3 · 1 · 1 = 𝜋 2 2 + 𝜋 3
ambos genes recesivos (𝑎𝑎 que se puede simbolizar por 𝑅) es:
𝑃( 𝑅 𝑡+1 | 𝐷 𝑡 ) = 𝑝 13 = 0
Como el individuo hereda un gen dominante del padre con probabilidad 1, entonces es imposible que llegue a tener ambos genes recesivos.
b) Si el padre tiene un gen dominante y el otro recesivo, y escoge a una madre para cruzarse, la probabilidad de que el hijo tenga:
ambos genes dominantes (𝐷) es:
𝑃 𝐷 𝑡+1 𝐻 𝑡 = 𝑝 21 = 𝑞 1 𝑞 𝐷1 𝑝 𝐷 + 𝑞 2 𝑞 𝐷2 𝑝 𝐷 + 𝑞 3 𝑞 𝐷3 𝑝 𝐷
𝑝 21 = 𝜋 1 ·1· 1 2 + 𝜋 2 · 1 2 · 1 2 + 𝜋 3 ·0· 1 2 = 𝜋 1 2 + 𝜋 2 4
un gen dominante y otro recesivo (𝐻) es:
𝑃 𝐻 𝑡+1 𝐷 𝑡 = 𝑝 22 = 𝑞 1 𝑞 𝐷1 𝑝 𝑅 + 𝑞 2 ( 𝑞 𝐷2 𝑝 𝑅 + 𝑞 𝑅2 𝑝 ?? ) 𝑝 𝐷 + 𝑞 3 𝑞 𝑅3 𝑝 𝐷
𝑝 22 = 𝜋 1 ·1· 1 2 + 𝜋 2 · 1 2 · 1 2 + 1 2 · 1 2 + 𝜋 3 ·1· 1 2 = 1 2
ambos genes recesivos (𝑅)
𝑃 𝑅 𝑡+1 𝐻 𝑡 = 𝑝 23 = 𝑞 1 𝑞 𝑅1 𝑝 𝑅 + 𝑞 2 𝑞 𝑅2 𝑝 𝑅 + 𝑞 3 𝑞 𝑅3 𝑝 𝑅
𝑝 23 = 𝜋 1 ·0· 1 2 + 𝜋 2 · 1 2 · 1 2 + 𝜋 3 ·1· 1 2 = 𝜋 2 4 + 𝜋 3 2
c) Si el padre tiene ambos genes recesivos, y escoge a una madre para cruzarse, la probabilidad de que el hijo tenga ambos genes dominantes (D) es:
𝑃 𝐷 𝑡+1 𝑅 𝑡 = 𝑝 31 =0
Puesto que el individuo hereda un gen recesivo del padre con probabilidad 1, entonces es imposible que llega a tener ambos genes dominantes.
un gen dominante y otro recesivo (𝐻) es:
𝑃 𝐻 𝑡+1 𝑅 𝑡 = 𝑝 32 = 𝑞 1 𝑞 𝐷1 𝑝 𝑅 + 𝑞 2 𝑞 𝐷2 𝑝 𝑅 + 𝑞 3 𝑞 𝐷3 𝑝 𝑅
𝑝 22 = 𝜋 1 ·1·1+ 𝜋 2 · 1 2 ·1+ 𝜋 3 ·0·1 = 𝜋 1 + 𝜋 2 2
ambos genes recesivos (𝑅)
𝑃 𝑅 𝑡+1 𝑅 𝑡 = 𝑝 33 = 𝑞 1 𝑞 𝑅1 𝑝 𝑅 + 𝑞 2 𝑞 𝑅2 𝑝 𝑅 + 𝑞 3 𝑞 𝑅3 𝑝 𝑅
𝑝 33 = 𝜋 1 ·0·1+ 𝜋 2 · 1 2 ·1+ 𝜋 3 ·1·1 = 𝜋 2 2 + 𝜋 3
Con los resultados anteriores, la matriz de transición de probabilidades es:
y la distribución de probabilidad de la variable aleatoria 𝑋 𝑡 (de los estados) en el tiempo 𝑡, ∀ 𝑡∈{1,2,3,…}, es:
𝑉 𝑡 = 𝛱 1 . 𝑃 (𝑡−1) = 𝜋 1 + 𝜋 2 2 2 , 2 𝜋 1 + 𝜋 2 2 𝜋 2 2 + 𝜋 3 , 𝜋 2 2 + 𝜋 3 2 (13)
Esto nos dice que esta cadena de Markov alcanza ya su condición estable en el tiempo t=1, es decir, que con la primera generación de descendientes ya se alcanza el equilibrio entre los genotipos.
Diploide con dos pares de genes independientes
En sus anotaciones Mendel dejó constancia de que también estudió en detalle el diploide con dos y tres pares de genes. En estos estudios dedujo que las elecciones de los gametos de cada carácter en cada generación eran independientes. El caso del diploide con dos pares de genes consiste en tomar los caracteres textura de las semillas cuyas categorías son lisa (A) y rugosa (a), y color de las semillas con categorías amarilla (B) y verde (b), simultáneamente. En el genotipo, las semillas pueden estar según la Tabla 3 en un nivel sobre el siguiente conjunto de estados:
?? = {𝐴𝐴𝐵𝐵,𝑎𝐴𝐵𝐵,𝑎𝑎𝐵𝐵,𝐴𝐴𝑏𝐵,𝑎𝐴𝑏𝐵,𝑎𝑎𝑏𝐵,𝐴𝐴𝑏𝑏,𝑎𝐴𝑏𝑏,𝑎𝑎𝑏𝑏}
Si 𝑋 𝑡 es la variable aleatoria que representa el estado sobre la cual se encuentra el genotipo en el instante 𝑡, se tendrá que la distribución de probabilidad de los estados de este proceso de autofecundación en el tiempo 𝑡 será 𝑉 𝑡 =( 𝑣 𝑡 1 , 𝑣 𝑡 2 ,…, 𝑣 𝑡 9 ), con 𝑖∈{1,2,...,9}, 𝑡∈{1,2,...} y 𝑣 𝑡 𝑖 =𝑃( 𝑋 𝑡 =𝑖). En este caso, Mendel notó que si tomaba semillas con líneas puras y las autofecundaba, en la próxima generación todas las semillas eran de la misma línea pura tomada. Además, si consideraba semillas que no eran de líneas puras se daban las siguientes situaciones.
Si las semillas consideradas tienen genotipos 𝑎𝐴𝐵𝐵 y se autofecundan se tienen tres tipos posibles de genotipos que son: 𝑎𝑎𝐵𝐵, 𝑎𝐴𝐵𝐵 y 𝐴𝐴𝐵𝐵.
Tomando en consideración la Tabla 4 se tiene:
𝑃 𝐴𝐴𝐵𝐵 𝑎𝐴𝐵𝐵 = 𝑝 21 = 1 4 , 𝑃 𝑎𝐴𝐵𝐵 𝑎𝐴𝐵𝐵 = 𝑝 22 = 1 2 , 𝑃(𝑎𝑎𝐵𝐵|𝑎𝐴𝐵𝐵)= 𝑝 23 = 1 4
Si las semillas consideradas tienen genotipos 𝐴𝐴𝑏𝐵 y se autofecundan se tienen tres tipos posibles de genotipos que son: 𝐴𝐴𝑏𝑏, 𝐴𝐴𝑏𝐵 y 𝐴𝐴𝐵𝐵. (Tabla 5)
𝑃 𝐴𝐴𝐵𝐵 𝐴𝐴𝑏𝐵 = 𝑝 41 = 1 4 , 𝑃 𝐴𝐴𝑏𝐵 𝐴𝐴𝑏𝐵 = 𝑝 44 = 1 2 ,𝑃(𝐴𝐴𝑏𝑏|𝑎𝐴𝐵𝐵)= 𝑝 73 = 1 4
Si las semillas consideradas tienen genotipos 𝑎𝐴𝑏𝐵 y se autofecundan se tienen nueve tipos posibles de genotipos que son: 𝑎𝑎𝑏𝑏, 𝑎𝑎𝑏𝐵,𝑎𝐴𝑏𝑏,𝑎𝐴𝑏𝐵, 𝑎𝑎𝐵𝐵, 𝑎𝐴𝐵𝐵, 𝐴𝐴𝑏𝑏, 𝐴𝐴𝑏𝐵 y AABB. (Tabla 6)
Tabla 6: Genotipos resultantes de un cruzamiento aAbB x aAbB
| Gametas | ab | aB | Ab | AB |
|---|---|---|---|---|
| ab | aabb | aabB | aAbb | aAbB |
| aB | aabB | aaBB | aAbB | aABB |
| Ab | aAbb | aAbB | AAbb | AAbB |
| AB | aAbB | aABB | AAbB | AABB |
𝑃(𝐴𝐴𝐵𝐵|𝑎𝐴𝑏𝐵)= 𝑝 51 = 1 16 , 𝑃(𝑎𝐴𝐵𝐵|𝑎𝐴𝑏𝐵)= 𝑝 52 = 1 8 , 𝑃(𝑎𝑎𝐵𝐵|𝑎𝐴𝑏𝐵)= 𝑝 53 = 1 16
𝑃(𝐴𝐴𝑏𝐵|𝑎𝐴𝑏𝐵)= 𝑝 54 = 1 8 , 𝑃(𝑎𝐴𝑏𝐵|𝑎𝐴𝑏𝐵)= 𝑝 55 = 1 4 , 𝑃(𝑎𝑎𝑏𝐵|𝑎𝐴𝑏𝐵)= 𝑝 56 = 1 8
𝑃(𝐴𝐴𝑏𝑏|𝑎𝐴𝑏𝐵)= 𝑝 57 = 1 16 , 𝑃(𝑎𝐴𝑏𝑎|𝑎𝐴𝑏𝐵)= 𝑝 58 = 1 8 , 𝑃(𝑎𝑎𝑏𝑏|𝑎𝐴𝑏𝐵)= 𝑝 59 = 1 16
si las semillas consideradas tienen genotipos aabB y se autofecundan tendremos tres tipos posibles de genotipos que son: 𝑎𝑎𝑏𝑏, 𝑎𝑎𝑏𝐵 y aaBB. (Tabla 7)
Tabla 7: Genotipos resultantes de un cruzamiento aabB x aabB
| Gametas | ab | aB |
|---|---|---|
| ab | aabb | aabB |
| aB | aabB | aaBB |
𝑃(𝑎𝑎𝐵𝐵|𝑎𝑎𝑏𝐵)= 𝑝 63 = 1 4 , 𝑃(𝑎𝑎𝑏??|𝑎𝑎𝑏𝐵)= 𝑝 66 = 1 2 , 𝑃(𝑎𝑎𝑏𝑏|𝑎𝑎𝑏𝐵)= 𝑝 69 = 1 4
si las semillas consideradas tienen genotipos aAbb y se autofecundan tendremos tres tipos posibles de genotipos que son: 𝑎𝑎𝑏𝑏, 𝑎𝐴𝑏𝑏 y AAbb. (Tabla 8)
𝑃(𝐴𝐴𝑏𝑏|𝑎𝐴𝑏𝑏)= 𝑝 87 = 1 4 , 𝑃(𝑎𝐴𝑏𝑏|𝑎𝐴𝑏𝑏) = 𝑝 88 = 1 2 , 𝑃(𝑎𝑎𝑏𝑏|𝑎𝐴𝐵𝐵) = 𝑝 89 = 1 4
Como al inicio del estudio del diploide con dos pares de genes, se cruzó las líneas puras liso y verde cuyos genotipos eran AAbb con líneas puras rugoso y amarillo con genotipos aaBB, obteniendo en F1 semillas lisas y amarillas con genotipos aAbB, se tiene que la distribución inicial del proceso está dada por 𝜫 𝟐 =(0,0,0,0,1,0,0,0,0).
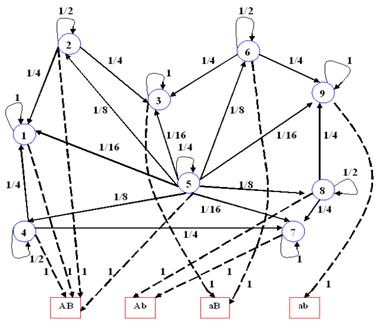
Al igual que en el caso del diploide con un solo par de genes, considerando que la distribución de los cromosomas es al azar, que las elecciones de los genes de carácter a carácter son independientes y que el tiempo de transición es homogéneo, se obtiene el digrafo de transición mostrado en la Figura 8 y la matriz de probabilidades de transición está dada por P 2 . En esta cadena de Markov los estados 1, 3, 7 y 9 son absorbentes, y los demás estados son transitorios. Realizando un procedimiento análogo al caso del diploide con un par de genes, y teniendo en cuenta el caso límite 𝑉 ∞ = 1 2 , 0, 1 2 y que 0=(0,0,0), se obtiene:
𝑉 𝑡 2 = 1 4 − 2 𝑡 −1 4 𝑡 , 2 𝑡−1 −1 2 2𝑡−1 , 1 4 − 2 𝑡 −1 4 𝑡 , 2 𝑡−1 −1 2 2𝑡−1 , 1 4 𝑡−1 , 2 𝑡−1 −1 2 2𝑡−1 , 1 4 − 2 𝑡 −1 4 𝑡 , 2 𝑡−1 −1 2 2𝑡−1 , 1 4 − 2 𝑡 −1 4 𝑡 (14)
𝑉 ∞ 2 = lim 𝑡→∞ 𝑉 𝑡 2 = 1 4 , 0, 1 4 ,0, 0, 0, 1 4 , 0, 1 4 = 1 2 ( 𝑉 ∞ , 0, 𝑉 ∞ ) (15)
Según el resultado obtenido, esta cadena markoviana será absorbida por alguno de los estados absorbentes intervinientes y, la población de semillas será rápidamente homogénea. Por lo tanto, la forma de dicha población corresponderá a alguna de las cuatro líneas puras tomadas.
Diploide con k pares de genes
Al analizar el diploide con k pares de genes todos independientes, se tiene que los genotipos pueden estar sobre un total de 3 𝑘 estados. La matriz de probabilidades de transición de este proceso markoviano es de orden 3 𝑘 × 3 𝑘 y estará dada por:
siendo 𝑃 𝑘−1 la matriz de probabilidades de transición de orden 3 𝑘−1 × 3 𝑘−1 que se obtiene en el caso del diploide con 𝑘 −1 pares de genes y 𝑂 es la matriz nula de orden 3 𝑘−1 × 3 𝑘−1 . La distribución inicial será
𝜫 𝒌 =(0,...,1,...,0) en dirección del eje 3 𝑘+1 2 , con 𝛱 𝑘 ∈ |R 3𝑘 .
Al realizar procedimientos análogos a los anteriores para cada 𝑘∈{3,4,5,6,7} se obtiene que la distribución límite está dada por:
𝑉 ∞ 𝑘 = 1 2 ( 𝑉 ∞ 𝑘−1 , 0, 𝑉 ∞ 𝑘−1 ) (16)
donde 𝑉 ∞ 𝑘−1 es la distribución límite para el caso del diploide con k-1 pares de genes independientes uno del otro.
Experimentos mendelianos como cadenas de Markov
Mendel, mediante experimentos, dedujo que era preciso distinguir la constitución genética (genotipo) de un individuo de su característica visible (fenotipo). Este hecho muestra que en los experimentos mendelianos interviene un proceso visible consistente en los fenotipos observados en los individuos en cada generación y un proceso oculto basado en los genotipos de los individuos en cada generación.
Modelo HMM para el diploide con un solo par de genes
En la sección anterior, se ha visto que el proceso oculto es una cadena de Markov con espacio de estados 𝑆={𝐴𝐴 (𝑒𝑠𝑡𝑎𝑑𝑜 1), 𝑎𝐴 (𝑒𝑠𝑡𝑎𝑑𝑜 2), 𝑎𝑎 (𝑒𝑠𝑡𝑎𝑑𝑜 3)}, matriz de transición de probabilidades de un paso
y distribución de probabilidad inicial 𝜫 𝟏 =( 0, 1, 0 ).
El proceso visible consiste en un proceso estocástico con dos estados, los fenotipos “color amarillo (A)” y color “verde (a)”. Para determinar la probabilidad de que se observe el fenotipo k dado que el individuo se tiene genotipo del tipo 𝑖, 𝑏 𝑖 (𝑘), ∀𝑖∈{1,2,3} y ∀𝑘∈{𝑎,𝐴} se sigue el siguiente procedimiento:
Si el individuo se encuentra en el estado 1, su genotipo es homocigota dominante (AA), las plantas con semillas de color amarilla siempre dan semillas de color amarilla y por lo tanto, 𝑏 1 (𝐴) = 1 y 𝑏 1 (𝑎) = 0.
Si el individuo se encuentra en el estado 2, su genotipo es heterocigota (aA), entonces, las semillas se verán de color amarilla debido a que este color amarillo (A) es dominante y por lo tanto, 𝑏 1 (𝐴) = 1 y 𝑏 1 (𝑎) = 0.
Si el individuo se encuentra en el estado 3, su genotipo es homocigota recesivo (aa), las plantas con semillas de color verde siempre dan semillas de color verde y por lo tanto, 𝑏 1 (𝐴) = 0 y 𝑏 1 (𝑎) = 1.
Del procedimiento anterior, la matriz de probabilidades de emisión de las observaciones está dada por:
y el modelo oculto de Markov obtenido queda totalmente especificada por el conjunto de parámetros 𝜆 = ( 𝐀 𝟏 , 𝐁 𝟏 , 𝜫 𝟏 ).
Modelo HMM para el diploide con dos pares de genes independientes
Mendel al considerar los caracteres textura y color de las semillas obtuvo nueve tipos diferentes de genotipos y cuatro de fenotipos, por lo que el proceso oculto, consistente en la autofecundación de las semillas en su genotipo, es una cadena de Markov con espacio de estados 𝑆 compuesto por los estados 𝐴𝐴𝐵𝐵 1 , 𝑎𝐴𝐵𝐵 2 , 𝑎𝑎𝐵𝐵 3 , 𝐴𝐴𝑏?? 4 , 𝑎𝐴𝑏𝐵 5 , 𝑎𝑎𝑏𝐵 6 , ,𝐴𝐴𝑏𝑏 7 , 𝑎𝐴𝑏𝑏 8 y 𝑎𝑎𝑏𝑏 9 , distribución inicial 𝜫 𝟐 =(0,0,0,0,1,0,0,0,0) y matriz de probabilidades de transición
En el proceso observable tenemos cuatro categorías que constituyen los tipos posibles de fenotipos que se observan en cada generación filial. Estas categorías son: liso y amarillo (AB), liso y verde (Ab), rugoso y amarillo (aB), rugoso y verde (ab). (Figura 9 ).
Considerando los genes dominantes liso (A) y amarillo (B) en los caracteres textura y color de las semillas respectivamente, se procede a formar la matriz de probabilidades de emisión de observaciones y con ello, verificar que observaciones podrán emitir los estados del proceso oculto. En primer lugar, si el proceso oculto se encuentra en los estados 𝐴𝐴𝐵𝐵, 𝑎𝐴𝐵𝐵, 𝐴𝐴𝑏𝐵 y aAbB con probabilidad 1 se observan semillas lisas y amarillas (AB). Por otro lado, si se consideran los estados AAbb y aBbb se tendrán semillas lisas y verdes (Ab). En el caso del estado aabb se tienen semillas rugosas y verdes (ab). Finalmente, estando en los estados aaBB y aabB se verán semillas rugosas y amarillas (aB). Con estos resultados, se tiene:
El modelo oculto de Márkov obtenido, bajo estas condiciones, queda totalmente especificada por el conjunto de parámetros 𝜆=(A2, B2, π2).
Conclusiones
Según las revisiones de los trabajos de reseña analizados, Mendel no tenía ningún conocimiento anterior de la naturaleza dual de los genes, pero a través de una serie de experimentos en el jardín de su convento pudo detectar la presencia de gen oculto y nombrarlo “Elemente”. La genética mendeliana se refiere a la transmisión de los rasgos biológicos discretos de una generación a otra y los modos de expresión de los genes.
La estadística y la teoría de probabilidad, constituyen las piezas fundamentales en la formación del marco teórico de los modelos ocultos de Márkov. Bajo este contexto, la matemática proporciona las herramientas necesarias para el planteamiento de soluciones a los distintos problemas que se presentan al momento de la formulación de un modelo oculto de Márkov.
La matemática y las leyes de la uniformidad de los híbridos de la primera generación filial, de la segregación y de la transmisión independiente constituyen los principales pilares en la formulación de los distintos modelos de Markov aplicados a los experimentos mendelianos. En este sentido, mediante cadenas de Márkov y cadenas ocultas de Márkov, considerando una cierta cantidad de genes, se han estudiado y modelado los experimentos genéticos mendelianos sobre la base de la libre fertilización obteniéndose muy buenos resultados.
En la formulación de la cadena de Markov realizada sobre un par de genes, se ha podido constatar que el proceso será absorbido rápidamente por alguno de los dos estados absorbentes intervinientes. Entonces, con la auto fertilización, una población se divide en una serie de líneas que rápidamente se vuelven muy homocigóticas y asintóticamente, ésta produce la autofecundación de dos genotipos puros lo que hace que todos los descendientes sean del mismo tipo. En el caso del diploide con dos pares de genes independientes, el proceso será absorbida por alguno de los cuatro estados absorbentes intervinientes y la población de semillas será de la forma correspondiente a alguna de estas cuatro líneas puras.
Por su parte, en la formulación de los modelos ocultos de Markov realizada sobre los casos del diploide con un solo par de genes y el de dos pares de genes independientes se ha podido constar que quedan totalmente especificados por el conjunto de parámetros; matriz de probabilidades de transición A, matriz de probabilidades de emisión de observaciones B y distribución inicial 𝜫.
Con todo lo expresado, se ha podido comprobar que, mediante el uso del álgebra, del cálculo, la teoría de probabilidad y las tres leyes de Mendel se puede aplicar de manera satisfactoria y eficiente la teoría de Markov, sobre la base de la libre fertilización, en el campo de la biología.
Agradecimientos
Al dueño eterno del reino, del poder y la gloria desde que el tiempo no tenía memoria. A este Divino Creador, cuya fuente de luz y de fuerza me impulsa a seguir adelante y me levanta cuando tropiezo por los caminos de la vida.
A mis padres y a mi amada familia por el apoyo de siempre. En especial a mi abuela Avelina por haberme guiado desde siempre por el largo sendero de la vida, a Francisca Ofelia, mis hijas Jessica Larissa y Lisset Fiorella, y mis hermanas Máxima y Nancy por el apoyo y confianza incondicional de siempre para el logro de mis metas y seguir mis ideales.
A la Dra. Ana Georgina Flesia por su orientación, paciencia y comprensión durante la realización de esta investigación.
Fuente de financiamiento
Fuente de financiamiento propia











 uBio
uBio