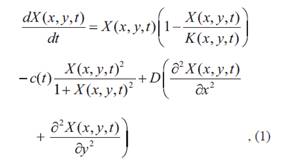Introducción

Los ecosistemas están expuestos a cambios graduales en sus condiciones ambientales como la temperatura, los niveles de precipitación, la disponibilidad de nutrientes, la diversidad de especies, etc. Aunque suele asumirse que la respuesta de los ecosistemas a estos cambios también es gradual, se ha demostrado que cambios ligeros en estas condiciones pueden llevar a cambios de régimen catastróficos, es decir, transformaciones drásticas en la estructura y funcionamiento de los ecosistemas. Estas transiciones a menudo están acompañadas de consecuencias ecológicas y socioeconómicas negativas y, además, muy difíciles de predecir y revertir (^{Scheffer et al., 2001}). Los cambios de régimen no solo pueden llevar a ecosistemas degradados, sino también a sociedades empobrecidas (^{Cooper et al., 2020}).

Modelos teóricos han dado lugar al establecimiento de métodos de alerta temprana ante cambios de régimen catastróficos. Se han propuesto diferentes indicadores, todos asociados a observables macroscópicos como la correlación varianza espa cial y temporal de la densidad de vegetación (^{Fort et al., 2010}; ^{Dakos et al., 2010}), la emergencia de patrones particulares en la distribución espacial de la vegetación (^{Kéfi et al., 2014}) y la ralentización en los tiempos de recuperación de los ecosistemas (ralentización crítica), siendo esta última la más difícil de medir, pues requiere un muestreo continuo y de larga duración, lo que puede resultar prohibitivo en cuanto a costos y tiempo. El análisis espacial, por su lado, se presenta como la opción más viable. Considerando la relación entre características espaciales de la vegetación y las transiciones a es tados desertificados, Kéfi et al. (2014) han sugerido una metodología de análisis basada prioritariamente en información espacial de la vegetación en eco- sistemas áridos y semiáridos. Esta metodología recomienda primeramente clasificar el ecosistema en función al tipo de patrón espacial que presenta la vegetación y, a partir de esta clasificación, se proponen los indicadores espaciales más convenientes para la detección de cambios de régimen catastróficos, considerando los mecanismos de interacción asociados a la emergencia de cada tipo de patrón espacial.

Además del desarrollo de indicadores y señales de alerta temprana, existe también una creciente literatura sobre manejo y mitigación del impacto de cambios de régimen catastróficos en ecosistemas áridos y semiáridos, en bosques tropicales e incluso en la explotación de pasturas para emprendimientos ganaderos (^{Fort et al., 2010}; ^{Dieguez y Fort, 2017}; ^{Vidiella et al., 2018}; ^{Vidiella et al., 2020}; ^{van den Elsen et al., 2020}; ^{Fort et al., 2021}; ¹). Estas propuestas se valen no solo de datos de campo, sino también de modelos teóricos que contemplan los principales mecanismos de interacción entre elementos de un ecosistema, permitiendo estudiar escenarios y definir estrategias para la prevención, manejo, y/o mitigación de cambios de régimen mediante simulaciones computacionales. La literatura sobre cambios de régimen catastróficos se concentra principalmente en ecosistemas áridos y semiáridos, esto debido a la vulnerabilidad que presentan estos ecosistemas ante la desertificación. En Paraguay, los niveles de precipitación de la mayor parte del territorio hacen poco plausibles procesos de desertificación catastróficos como los estudiados en la literatura actual, no obstante, una excepción es la región noroeste del Chaco paraguayo, donde se encuentra la ecorregión Médanos del Chaco. Esta ecorregión alberga el Parque Nacional Médanos del Chaco, la segunda área protegida más grande de la Región Occidental (Gill et al., 2020). Los niveles de precipitación registrados en la región alcanzan los 400-500 mm anuales, los más bajos del país, y la permanencia de cuerpos de agua es también de las más bajas. Además, en esta región-así como en una parte importante del noroeste del Chaco- se miden los mayores promedios anuales de velocidad de viento del país: aproximadamente 6,5 m/s a 80 m de altura (Gill et al., 2020); el viento, al arrastrar las capas superficiales de tierra fértil, es un factor agravante de la degradación del suelo. Estas características vuelven a Médanos del Chaco una ecorregión sumamente vulnerable. Si bien existen estudios sobre sus características climáticas y ecológicas, se desconocen estudios dentro del marco teórico y metodológico de los cambios de régimen.

En este trabajo se estudiaron las características espaciales de la vegetación de Médanos del Chaco, enmarcando el análisis en la teoría de cambios de régimen catastróficos. Combinando el análisis espacial a partir de imágenes satelitales y los resultados obtenidos mediante simulaciones computacionales, se buscó determinar el estado actual del ecosistema respecto a un proceso de cambio de régimen catastrófico. Los resultados obtenidos muestran que los patrones espaciales observados en la vegetación son compatibles con un sistema en la región de transición a un régimen de baja densidad de vegetación (desértico). No obstante, estos resultados deben considerarse como una primera aproximación al estudio de cambios de régimen catastróficos en este ecosistema, requiriéndose estudios más detallados y el desarrollo de modelos más elaborados que permitan contrastar, en varios frentes, los procesos teóricos con la evidencia empírica.

Materiales y métodos

La investigación fue desarrollada en tres etapas: la primera consistió en la obtención y análisis de imágenes aéreas y/o satelitales; la segunda en la generación de patrones de distribución de vegetación a partir de simulaciones computacionales de un modelo mínimo, y la tercera, en una comparación entre la estructura espacial de los parches de vegetación observados en campo y en el modelo.

Para la recopilación de las imágenes satelitales se consideró una región circular de 14 km de diámetro dentro del Parque Nacional Médanos del Chaco. A través de Google Earth Pro se seleccionaron manualmente 5 imágenes (sin superposición) ^{Google Earth, 2008a}; ^2008b; ^2008c; ^200d; ^2008e de diferentes zonas de esta región, todas tomadas en septiembre del año 2008, con cada imagen cubriendo aproximadamente 1,13 km² de terreno. Las referencias de estas imágenes se incluyen en la sección de referencias de esta publicación. Posteriormente, las imágenes fueron binarizadas.

La binarización constó de dos partes: primero, la normalización e inversión del canal R (rojo en el modelo de color RGB) y, luego, el establecimiento de un valor umbral de densidad de vegetación Xu que separe las fases de vegetación y de suelo des- nudo. El objetivo de la normalización de uno de los canales RGB es asociar la “intensidad” de color en cada píxel con un valor de densidad de vegetación mediante un número adimensional entre 0 y 1 (ver Figura 1.b). Se normalizó el canal R debido a que se obtuvieron mejores resultados que con los canales G y B. Aun cuando los canales RGB no responden a longitudes de onda específicas del espectro electromagnético, la inversión del canal R se fundamentó en la siguiente suposición: el color rojo es reflejado en mayor medida por el suelo desnudo y absorbido en mayor medida por la vegetación, por lo tanto, valores bajos de R indicarían presencia de vegetación, y valores altos, suelo desnudo. Xu se determinó mediante el método de Multi-Otsu (^{Liao et al., 2001}) disponible en el paquete Scikit-Image para lenguaje Python. Este método segmenta las imágenes en tres fases (ver Figura 1.c), considerando dos valores umbral; para obtener solo dos fases, se definió a Xu como el menor de estos valores. Así, valores de densidad de vegetación inferiores a Xu indican suelo desnudo y valores superiores indican presencia de vegetación (ver Figura 1.d).

Una vez binarizadas las imágenes, se determinó la distribución de tamaños de los parches, no siendo considerados los parches que atraviesan la imagen de extremo a extremo (parches percolantes) -una práctica común en teoría de percolación. La obtención de la distribución de probabilidad de áreas de los parches permite comparar las observaciones en campo con las estructuras de parches vistas en el modelo mínimo. La distribución obtenida fue ajustada a una ley de potencia o función potencial P(A)=cA ^-γ , donde A es el tamaño de cada parche, P es la probabilidad de ocurrencia asociada a un cierto tamaño, γ es el exponente crítico de la función y c es una constante de proporcionalidad. El ajuste se llevó a cabo mediante el método de mínimos cuadrados utilizando el paquete estadístico Scipy para lenguaje Python. Un procedimiento similar al utilizado aquí fue aplicado por ^{Meloni et al. (2019}) para el estudio de la distribución de parches de vegetación en ecosistemas semiáridos del sur de España y Estados Unidos.

Considerando que la búsqueda por leyes de potencia en datos de campo y/o experimentales es problemática (Buchanan, 2008), y a día de hoy no existe consenso respecto a cómo debe encararse el análisis estadístico. Para una descripción más detallada de las estructuras de parches observadas en campo y en el modelo, se calcularon la probabilidad de que un sitio esté ocupado por vegetación y la probabilidad de que un sitio aleatorio pertenezca al parche percolante. La primera es conocida en la literatura de teoría de percolación como densidad de ocupación ρ, mientras que la segunda, como fuerza P del parche infinito (^{Stauffer y Aharony, 1994}).

Figura 1 Binarización de imágenes. a) Recorte de imagen original obtenida de Google Earth. b) Imagen del canal R normali zado e invertido en escala de verdes. c) Segmentación mediante método de Multi-Otsu. Se obtienen tres fases: suelo desnudo (blanco), vegetación de baja densidad (marrón) y vegetación de alta densidad (verde). d) Imagen binarizada. Se obtienen dos fases: suelo desnudo (blanco) y vegetación (negro). Fuente: adaptado de Google Earth, 2008. 

Finalmente, se determinaron también la correlación espacial C ₂ y la varianza espacial σx de los parches en las imágenes binarizadas y en el modelo, y se evaluó el comportamiento cualitativo de estos parámetros en función a diferentes densidades de ocupación.

La correlación espacial y la varianza espacial son importantes indicadores de una transición de fase, ya que los modelos teóricos muestran un máximo en ambos observables en el punto crítico de una transición (^{Fort et al., 2010}; ^{Dakos et al., 2010}). Siguiendo la recomendación de Dakos et al. (2010), en este estudio se optó por utilizar el coeficiente de Moran como medida de correlación espacial.

Para la elección de un modelo teórico capaz de describir un cambio de régimen catastrófico se buscó simplicidad y el menor número posible de parámetros libres. Bajo estos criterios se optó por un modelo mínimo (^{Fort et al., 2010}) definido por la ecuación

Donde X es la densidad de vegetación o densidad de biomasa (variable de estado), K es la capacidad de carga del sistema, c es la tasa de consumo o decaimiento de la vegetación y D es un coeficiente de difusión.

El modelo descrito por la ecuación (1) sin el término difusivo, fue propuesto inicialmente por ^{Noy-Meir (1975}) y ^{May (1977}) para describir la transición de un sistema de pastura bajo sobreexplotación cuando se supera un umbral crítico en la tasa de consumo c. No obstante, el modelo es capaz de describir de forma sencilla la dinámica de una población biológica independientemente del sistema. El primer término describe un crecimiento logístico acotado por la capacidad de carga del sistema, el segundo, la tasa de consumo, muerte o decaimiento de la población, y el tercer término es un término difusivo que introduce interacción espacial en el modelo, donde D es el parámetro que determina la conectividad del sistema (^{Dakos et al., 2010}).

Además de la búsqueda de simplicidad, la elección del modelo y del parámetro de control se fundamentó en algunas hipótesis. Por un lado, se parte de la posibilidad de que Médanos podría presentar distribuciones de tamaños de parches de vegetación libres de escala. Además, es razonable suponer que en condiciones de escasez de recursos como agua o nutrientes existe una relación entre el decrecimiento de la capacidad de carga y la emergencia de mecanismos de reorganización determinantes para la formación de patrones libres de escala -patrones que han sido reportados anteriormente en el modelo seleccionado (^{Fort, 2010}). Por otro lado, la tasa de consumo o decaimiento c se considera baja y de variabilidad mínima, pues no existen allí actividades humanas de explotación ganadera y forestal; a partir de esto puede considerarse que variaciones en la densidad de vegetación, así como posibles cambios de régimen, se deberían principalmente a cambios en la capacidad de carga del ecosistema.

Así, se supone que el modelo seleccionado es adec uado y se propone al valor medio de K (x, y) como, (parámetro de control en las simulaciones.

Las simulaciones se realizaron mediante la implementación del modelo como autómata celular (^{Fort, 2020}). Se mantuvieron valores de c menores a 1.8 y valores de d entre 0.1 y 0.3. Los valores de los elementos de la matriz de capacidad de carga K (x, y) son aleatorios y se obtienen a partir de una distribución uniforme con valores en el intervalo [〈K〉 - δK, 〈K 〉 + δK], siendo 〈K〉 la capacidad de carga media y δK = 0.5. La simulación se efectuó inicializando el sistema con una capacidad de carga media igual a 10, iterando el sistema por 500 pasos de tiempo para permitir su estabilización. Luego, durante 1000 iteraciones, se procedió a reducir gradualmente la capacidad de carga media hasta alcanzar un valor de 4, simulando la transición de un estado de alta densidad de vegetación a uno de baja densidad. Seguidamente, durante las próximas 1000 iteraciones, se volvió a incrementar la capacidad de carga media hasta alcanzar el valor inicial 10; de esta manera se obtiene información sobre la transición inversa, es decir, de un régimen de baja densidad a uno de alta densidad (ver Figura 2). El mismo procedimiento se repitió 100 veces para la obtención de una muestra representativa de la estructura de los parches de vegetación que emergen durante la transición de régimen.

Se analizó la estructura de parches en cinco puntos en la región de transición de alta a baja densidad de vegetación: el correspondiente al punto crítico (definido como el valor medio de K para el cual la varianza σx ² es máxima), dos puntos subcríticos (pertenecientes a la región de transición y anteriores al punto crítico) y dos puntos super-críticos (pertenecientes a la región de transición y posteriores al punto crítico); estos se indican en el diagrama de bifurcación presentado en la Figura 2. Finalmente, para cada configuración espacial obtenida se determinó la distribución de las áreas de los parches.

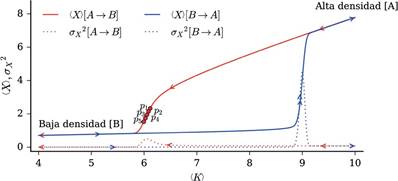
Figura 2 Diagrama de bifurcación del modelo para d = 0.2 y c = 1.75. Las curvas continuas corresponden a la densidad de vegetación promedio 〈X〉, y las curvas discontinuas, a la varianza espacial σx ². Se visualizan trayectorias de un régimen de alta densidad de vegetación a uno de baja densidad (en rojo) y de baja densidad a alta densidad (en azul). Es posible observar el fenómeno de histéresis, en el que la transición del régimen de alta a baja densidad sigue una trayectoria distinta al caso opuesto (baja-alta). En la región intermedia (〈K〉 entre 6 y 9) existen dos estados estables alternativos, uno de alta densidad y otro de baja densidad 

Figura 3 Distribución de tamaños de parches de vegetación para las imágenes satelitales. Puntos: medidas experimentales. Línea celeste: curva de ajuste (ley de potencia) 

Para obtener la fuerza del parche percolante, la correlación espacial y la varianza espacial en función a la capacidad de carga y la densidad de ocupación se analizaron todos los puntos en el intervalo de capacidad de carga media de 7 a 5 de la transición A a B.

Resultados y discusión

Distribución de áreas de parches de vegetación

En la Figura 3 se presenta la distribución obtenida para las imágenes satelitales. En el eje horizontal se indica el área A (en m²) de los parches de vegetación, y en el eje vertical, la probabilidad P de que un parche escogido al azar tenga un tamaño A; ambos ejes son mostrados en escala logarítmica. Los puntos representan las medidas experimentales, y la recta, la curva de ajuste definida por una función potencial P α A ^-γ . Se observó que la distribución de probabilidad de las áreas sigue una ley de potencia en más de tres décadas (10⁰ a 10³ m²) con un coeficiente de determinación superior a 0.98. Esto podría ser un indicador de un patrón de vegetación libre de escala, característico durante cambios de régimen (^{Fort et al., 2010}; ^{Kéfi et al., 2014}).

Las distribuciones obtenidas mediante simulaciones del modelo mínimo para cada uno de los puntos analizados se muestran en la Figura 4. Como era esperado, la distribución de parches de vegetación en el punto crítico p ₃ presenta una distribución en ley de potencia en un rango de más de 3 décadas, un comportamiento conocido para el modelo en cuestión (^{Fort et al., 2020}).

Figura 4 Distribuciones de tamaños de parches para d = 0.1 y c = 1.72. Puntos negros: distribución para el punto crítico (p ₃). Puntos azulados: distribuciones de áreas para puntos supercríticos 〈K〉 ≥ 〈K〉c. Puntos rojizos: distribuciones para puntos subcríticos 〈K〉 ≤ 〈K〉c. Las áreas se miden en unidades cuadradas de celda 

Distribuciones para puntos críticos (P3) en simulaciones con diferentes valores de conectividad d = 0.1, d = 0.2 y d = 0.3 (manteniendo c = 1.75) con sus correspondientes curvas de ajuste y valores de γ y R ² se presentan en la Figura 5. Las distribuciones se muestran similares a las observadas en campo, principalmente para los casos d = 0.1 y d = 0.2, donde la diferencia entre exponentes observados en campo y simulados es de apenas 0.02; luego, la distribución espacial observada en la vegetación de Médanos posee características que encajan con las distribuciones correspondientes a estados de vegetación en el entorno de la región crítica (cambio de régimen).

Estos resultados son similares a los resultados teóricos obtenidos por ^{Kéfi et al. (2007}) al estudiar ecosistemas áridos del Mediterráneo. En dicho trabajo se analizó la distribución de tamaños de parches de vegetación empleando un modelo de autómata celular de mayor complejidad que el modelo mínimo. Las distribuciones de áreas teóricas para un sistema con alta interacción local positiva (que involucra facilitación local y dispersión de semillas) y baja presión de pastoreo corresponden a leyes de potencia con exponentes entre 1.75 y 1.77, valores próximos a los observados para datos de campo en Médanos y en las simulaciones del modelo mínimo.

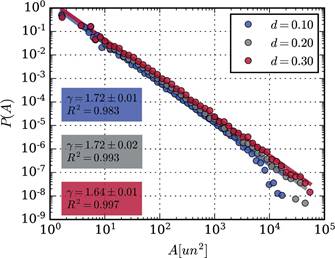
Figura 5 Distribuciones de tamaños de parches para c = 1.75 y distintos valores de coeficiente de conectividad d. Azul: d = 0.10. Gris: d = 0.20. Rojo: d = 0.30. Se muestran los exponentes obtenidos y el coeficiente de determinación. Para coeficientes de conectividad baja se obtiene el mismo exponente y cercano a lo observado en campo 

Es importante resaltar que la distribución de áreas obtenida por ^{Kéfi et al. (2007}) mediante mediciones de campo en Gata-Níjar, España (una de las regiones más secas de Europa), en Uta, Grecia y Timahdite, Marruecos, se observan leyes de potencia menos claras (ajustadas a menos de una década) con exponentes inferiores a 1.3, una diferencia mayor a 0.4 a los exponentes teóricos obtenidos mediante el modelo propuesto por los autores. En efecto, tanto el modelo mínimo utilizado en esta investigación como el modelo propuesto por Kefi et al. (2007) coinciden con una diferencia menor a 0.05 con los datos de campo observados en Médanos; en todos los casos el exponente que caracteriza la ley de potencia se encuentra en un intervalo entre 1.72 y 1.77. Proponemos aquí que esto se debe a que en los ecosistemas áridos y semiáridos del Mediterráneo estudiados por Kéfi et al. (2007), la vegetación ya ha atravesado el estado crítico, es decir, los ecosistemas se encuentran en estados supercríticos en dirección a un régimen de baja densidad. Observe que la distribución correspondiente al punto p ₄ en la Figura 4 se ajusta a una ley de potencia apenas a una década y el exponente es menor a lo observado en el punto crítico. Estas características coinciden con lo observado en los ecosistemas del Mediterráneo. No obstante, al momento de interpretar estos resultados, habrá que tener en mente que la relación entre leyes de potencia y comportamiento crítico no es unívoca (Touboul y Destexhe, 2017) y los métodos utilizados para obtención de distribuciones de probabilidad en leyes de potencia son problemáticos (Buchanan, 2008). Los resultados referentes a leyes de potencia presentados aquí no están exentos de dichos problemas, por lo que se recomienda tomarlos apenas como un primer indicador, no riguroso, de un proceso de cambio de régimen. Los análisis de varianza y correlación espacial, así como el estudio de los parches percolantes, presentados a seguir, brindarán una visión más completa respecto a la relación entre modelo y observaciones de campo.

Correlación y varianza espacial de la vegetación

En la Figura 6 se observan dos estados con densidad de vegetación homogénea (fases): uno de alta densidad de vegetación, donde la densidad de ocupación es máxima (ρ = 1), y otro de baja densidad de vegetación, donde la densidad de ocupación es nula (ρ = 0, pues la densidad de vegetación es inferior al umbral Xu en toda la región L × L). En las regiones homogéneas vemos que tanto C ₂ como σ son nulas, mientras que presentan valores no nulos en la región de transición con un máximo en torno a la capacidad de carga crítica, región donde la fase del sistema no está bien definida, pues en esta región se tiene una coexistencia de fases caracterizada por una densidad de ocupación entre 0 y 1.

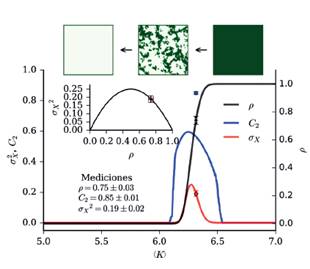
Figura 6 Correlación espacial, varianza espacial y densidad de ocupación en función a la capacidad de carga. Las curvas azul y roja corresponden a la correlación espacial C₂ y la varianza espacial σx ² obtenidas en las simulaciones. La curva negra corresponde a la densidad de ocupación ρ medida en las simulaciones. Se presentan en cuadros los patrones observados en los regímenes de alta (ρ = 1) y baja densidad (ρ = 0), así como el patrón en estado crítico (ρ = 0.5). Los puntos indican medidas en los Médanos incluyendo la incertidumbre. La figura interna muestra la relación entre la varianza y la densidad de ocupación observada en las simulaciones, mientras que el punto es el valor obtenido a partir de imágenes de los Médanos. Parámetros: c = 1.75 y d = 0.1 

El comportamiento observado puede explicarse mediante el siguiente razonamiento: en condiciones de abundancia de recursos el “agrupamiento” de la vegetación es menos necesario para su sobrevivencia, por lo que no se forman parches, dando como resultado una distribución espacial de vegetación homogénea y por ende, una correlación espacial nula. A medida que la disponibilidad de recursos disminuye, los mecanismos de interacción (como la facilitación local) provocan una redistribución de la vegetación (Rietkerk, 2004; ^{Kéfi et al., 2014}), aumentando el agrupamiento y, por lo tanto, la correlación espacial. Cuando los recursos disminuyen, la densidad de vegetación decrece de forma heterogénea, lo que se traduce en un aumento de la varianza espacial.

El comportamiento de C y σx ² para las imágenes satelitales es coherente con el comportamiento observado en las simulaciones en la región cerca de la transición. Si bien el valor exacto de C ₂ observado en campo es superior incluso al pico observado en simulaciones (C ₂ ≈ 0.6), en ambos casos se tiene alta correlación espacial (C ₂ ≥ 0.5), indicador de un cambio de régimen en el sistema (^{Dakos et al., 2010}; ^{Kéfi et al., 2014}). Para una misma densidad de ocupación, la varianza espacial observada en campo concuerda exactamente con la varianza espacial obtenida en las simulaciones (ver gráfico in- terno en Figura 6); esto permite ubicar el ecosistema de la zona estudiada de Médanos en el diagrama de bifurcación del modelo mínimo. Según este análisis, Médanos en el año 2008 (año de obtención de las las imágenes utilizadas) se encontraba en la región de cambio de régimen, no obstante, en un estado todavía subcrítico.

Diferentes regímenes en la percolación de parches de vegetación

En la Figura 7 se presenta la fuerza del parche percolante respecto a la densidad de ocupación obtenida en simulaciones y el valor medido en campo con su respectiva incertidumbre. Observamos que los valores medidos en campo caen aproximadamente sobre la curva simulada. Los parches percolantes observados en los Médanos presentan fuerza igual a Ps = 0.66 ± 0.08, mientras que la densidad de ocupación medida es igual a ρ = 0.74 ± 0.03, valores que al ser contrastados con los resultados obtenidos mediante simulación, coinciden con un sistema aproximándose al estado crítico, pero aún en un régimen levemente subcrítico. Estos resultados concuerdan con los obtenidos mediante el análisis de la varianza espacial presentado en la sección anterior.

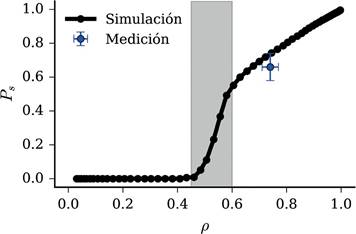
Figura 7 Fuerza del parche percolante vs. densidad de ocupación. La curva sólida son resultados obtenidos en simulaciones con tamaño de sistema L = 100, coeficiente de conectividad d = 0.1 y tasa de decaimiento c = 1.75. Los resultados pre- sentados corresponden a valores medios obtenidos a partir de 100 repeticiones. El punto azul corresponde a la fuerza y densidad media obtenida a partir de las 5 imágenes analizadas, se incluye la desviación estándar respecto a ambas medidas. Las observaciones de campo son coherentes con los resultados observados en la simulación. La región gris corresponde al régimen intermedio, donde se tiene la máxima sensibilidad de la fuerza del parche percolante a la densidad de ocupación 

En este modelo, el umbral de percolación (ρc) se encuentra en torno a 0.5, valor diferente al aso ciado a la clase de universalidad de percolación estándar, lo que es esperado, pues en este sistema, la probabilidad de ocupación de sitios distintos no son estadísticamente independientes, sino que se espera que estén correlacionadas. Discrepancias similares fueron encontradas por ^{Martín et al. (2020}), donde con un modelo teórico distinto, los autores mostraron que los parches de vegetación durante el cambio de régimen presentan características de per- colación distintas a la percolación estándar, además de ser dependientes de la densidad de vegetación y condiciones ambientales. Los autores afirman que este fenómeno es diferente al estudiado por la teoría de percolación tradicional, por lo tanto, su estudio presenta oportunidades de investigación teórica novedosas y relevantes.

Aun cuando el sistema no pertenezca a la clase de universalidad de percolación estándar, no se puede descartar la posibilidad de encontrar una nueva clase de universalidad capaz de describir este tipo de transiciones. Una investigación a favor de la existencia de una clase de universalidad en sistemas ecológicos fue presentada por ^{Meloni et al. (2019}). En el mismo, basándose en observaciones realizadas gracias a imágenes satelitales, los autores demostraron que el comportamiento de los patrones de vegetación en el semiárido del sur de España y del estado de Arizona en Estados Unidos son idénticos, evidencia de universalidad.

^{Meloni et al. (2019}) afirman que existen tres regímenes diferentes del sistema durante el cambio de régimen catastrófico, asociados a dos transiciones distintas. En el régimen A, régimen de baja densidad de vegetación, las propiedades geométricas de los parches muestran patrones aleatorios y esparsos, donde se maximiza los efectos de la escorrentía hídrica y se minimiza la infiltración de agua en el suelo. En el régimen B, la coalescencia (fusión) direcciona el crecimiento de los parches, lo que conlleva a tamaños y densidades no triviales. Los cambios en el arreglo espacial resultan del incremento en la conectividad de los parches, con consecuencias sobre la escorrentía superficial y favorecimiento de la infiltración de agua en el suelo. El proceso de coalescencia llevaría a la emergencia de parches percolantes provocando la saturación del proceso de coalescencia, lo que lleva a una transición, en este caso del régimen B al C. En el régimen C, emergen correlaciones de largo alcance a partir de los mecanismos de interacción en el ecosistema. La vegetación altamente conectada mitiga los efectos de la escorrentía y mejora considerablemente la absorción de agua por parte de la vegetación. Aquí, los detalles del terreno se hacen irrelevantes y los aspectos biológicos dominan los patrones presentes en la vegetación.

^{Meloni et al. (2019}) no proponen modelos para describir el fenómeno, no obstante, los resultados aquí presentados parecen coincidir respecto a la existencia de más de dos regímenes. Observando la fuerza de percolación respecto a la densidad (ver Figura 7), se observan tres regímenes caracterizados por diferencias en la pendiente de la fuerza de percolación respecto a la densidad de ocupación. El primero, régimen de fuerza nula, en el cual no existen parches percolantes; el segundo, donde la fuerza del parche percolante presenta una alta sensibilidad (pendiente grande) a la densidad de ocupación (aproximadamente entre 0.5 ≤ ρ ≤ 0.6); y el tercero, donde la sensibilidad a la densidad de ocupación se reduce considerablemente (ρ ≥ 0.6). Aunque el análisis realizado no buscó evidencias para confirmar la existencia de transiciones de fase de primer y segundo orden como lo observado por Meloni et al. (2019). Interpretaciones equivalentes respecto a la naturaleza de los regímenes observados pueden utilizarse aquí. El régimen intermedio, donde se tiene mayor sensibilidad de la fuerza de percolación a la densidad de ocupación, respondería al régimen B descrito anteriormente. En él, el au mento de la fuerza de percolación estaría asociado al proceso de coalescencia de parches menores, lo que ocurriría hasta un punto de saturación (ρ ≈ 0.6), en el cuál, ocurre la transición al tercer régimen, con características similares a la descrita por Meloni et al. (2019). En este contexto, ecosistemas en los Médanos, se encontrarían en el régimen C, no ob stante, estarían próximos a la transición al régimen B, donde los parches percolantes empiezan a reducir drásticamente su tamaño. Este proceso de reducción drástica estaría asociado al comprometimiento del papel de la vegetación en el control de la escorrentía hídrica, y en caso específico de los médanos, en la mitigación del impacto de la erosión eólica.

Los resultados presentados aquí indican que las características observadas en Médanos corresponden a lo esperado para un sistema en pleno proceso de cambio de régimen. No obstante, habrá que considerar las limitaciones de la metodología utilizada en esta investigación al momento de formar una opinión sobre el estado actual de Médanos. Las imágenes satelitales utilizadas aquí fueron del tipo RGB, por lo que el procedimiento de clasificación y binarización son menos robustos que los obtenidos con imágenes multiespectrales, donde índices como índice de vegetación por diferencia normalizada (NDVI) o el índice de agua por diferencia normal- izada (NDWI), pueden ser implementados para identificar y clasificar la vegetación de manera más precisa. Por ello, en trabajos futuros, se propone extender el análisis presentado aquí con imágenes multiespectrales de alta precisión y una validación en campo de la clasificación realizada.

Las imágenes de campo utilizadas en esta investigación datan de más de una década atrás, por lo que podría considerarse que los resultados presentados describen el estado pasado de la vegetación en los Médanos, luego las conclusiones de esta investigación están desfasadas. No obstante, el hecho de que la región estudiada pertenezca a un área protegida, con escasa actividad humana en sus entornos, permite suponer que los datos utilizados aún guardan actualidad. Los procesos de cambio de régimen ocurren a escalas de tiempo humanas (^{Cooper et al., 2020}), no obstante, estas transformaciones, una vez iniciadas, pueden llevar décadas para concluirse, siendo el fenómeno de ralentización crítica responsable por el retardo en la evolución del proceso (^{Vidiella et al., 2018}). Con esto, podemos esperar que los Médanos presenten todavía a día de hoy, patrones similares a los encontrados aquí.

Se propone tomar los resultados presentados aquí como primeros indicios de un cambio de régimen en Médanos del Chaco, afirmación que requiere estudios más detallados para ser corroborada o refutada. Se recomienda realizar campañas de monitoreo de larga duración que busquen indicios de un proceso de ralentización crítica. Considerando que experimentos in situ presentan costos prohibitivos, el procedimiento más viable consiste en realizar mediciones del tiempo de recuperación de la vegetación luego de eventos destructivos como grandes sequías e incendios. Esto podría realizarse mediante imágenes aéreas y/o satelitales tomadas a lo largo del tiempo, y brindaría evidencia contundente para la hipótesis de un cambio de régimen catastrófico en Médanos, pues la ralentización crítica sería evidencia sólida de un cambio de régimen catastrófico.

Conclusiones

Mediante el análisis de la distribución espacial de la vegetación en Médanos del Chaco y un modelo matemático mínimo, se identificaron características en terreno correspondientes a ecosistemas en proceso de cambio de régimen. La vegetación de Médanos presenta un patrón libre de escala, caracterizado por una distribución de área de parches en leyes de potencia, además de valores altos de correlación y varianza espacial, siendo todos estos indicadores de un cambio de régimen catastrófico. Los resultados parecen indicar que Médanos del Chaco se encuentra en pleno proceso de desertificación (transición a un sistema con baja densidad de vegetación). No obstante, las mediciones de varianza espacial vs. densidad de ocupación, y la presencia de parches percolantes con fuerza superior a 0.6, indican que el sistema aún no alcanzó el valor crítico para el cambio de régimen, siendo este un resultado esperanzador, pues permitiría definir estrategias para evitar la concreción del cambio de régimen o mitigar sus efectos en caso de que sea inevitable su ocurrencia.

Investigaciones relacionadas al manejo y mitigación de cambios de régimen catastróficos se basan no solo en observaciones de campo, sino que se sustentan en modelos teóricos que permiten dar sentido y contexto a los datos empíricos, evidenciando la utilidad de métodos provenientes de la física estadística y de la teoría de sistemas dinámicos no lineales en el desarrollo de herramientas cuantitativas que ayuden a enfrentar los desafíos existentes en la conservación de ecosistemas y uso de recursos naturales.

Este trabajo presenta un caso concreto donde datos de campo y modelado matemático se complementan para la identificación de procesos que a mediano y largo plazo amenazan los ecosistemas de una de las regiones más frágiles del centro del subcontinente sudamericano. Se recuerda que la desertificación de Médanos del Chaco no solo pone en riesgo la fauna y flora de esa región, sino que podría extenderse a regiones productivas del Chaco. Luego, estudios predictivos sobre estos procesos son de alta relevancia socioeconómica, claves para la sostenibilidad de las actividades humanas en la región.