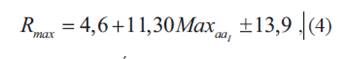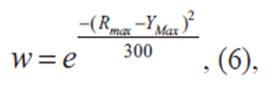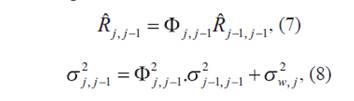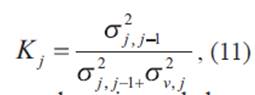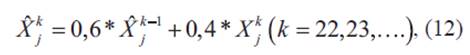Introducción

El estudio de las manchas solares data desde comienzos del siglo XIX mediante los pioneros trabajos de Rudolf Wolf del observatorio de Zúrich, posteriormente en Locarno (^{Cugnon, 1997}). Wolf propone que el índice relativo de manchas solares viene dado por:

R = k(10g + f) (1), donde g es el número de grupos de manchas observados en la fotósfera del sol y f el número de manchas individuales. En la ecuación anterior k es el factor de escala utilizado, este permite comparar con registros propios las observaciones realizadas por el SIDC (Solar Influences Data Center) de Bruselas-Bélgica, la AAVSO (American Association of Varialble Star Observers) y otros centros similares. El comportamiento de R en una base de tiempo del orden de años permite mejorar la precisión en la predicción de la mayoría de los índices de actividad solar, por lo tanto, es utilizado en aplicaciones a las relaciones solares-terrestres, así como a las predicciones de la relación frecuencia-ionósfera (^{Shapley, 1946}).

La actividad solar se relaciona con la densidad de iones en la parte superior de la atmósfera, y es por esto que influye en la propagación ondas de radio. Las predicciones de largo tiempo de la actividad solar son importantes para el planeamiento de las misiones espaciales, dado que la actividad solar determina el perfil de la densidad atmosférica y tiene una importante influencia en la trayectoria de satélites de órbita cercana a la tierra (Hanslmeier et al. 1999). Por otra parte, su comportamiento está relacionado con cambios climáticos severos como los eventos registrados en los siglos XVII y XIX con muy bajas temperaturas durante los periodos conocidos como mínimo de Maunder y Dalton, respectivamente. Recientes investigaciones sobre el campo magnético solar y terrestre sugieren que no hay razones para esperar un comportamiento similar a los mencionados anteriormente (^{Russell et al.2013}).

Diferentes técnicas predictivas de la actividad solar son utilizadas actualmente. Entre algunas que podemos mencionar se encuentran: el método de McNish- Lincoln (M&L), el método estándar (SM del inglés Standard Method) y el método combinado (CM del inglés Combined Method). Los dos primeros utilizan técnicas estadísticas basándose en ciclos previos al ciclo cuyo comportamiento se pretende predecir. El último método, utiliza datos como el índice geomagnético interplanetario aaI relacionado con el viento solar de alta velocidad cuyo comportamiento se encuentra desfasado con relación al ciclo de manchas solares. En general, este presenta un pico que ocurre antes del mínimo del ciclo entrante y permite una adecuada predicción para la amplitud del ciclo solar venidero ((^{Hathaway & Wilson, 2006}).

El CM asume que ciclos de la misma amplitud donde R es el número relativo de mancha solar tendrán una forma similar y de esta manera predice el comportamiento del próximo ciclo solar; el CM está completamente descrito en el trabajo de ^{Hanslmeier et al. (1999)}. Por otro lado, ^{Fessant et al. (1996}) han propuesto una técnica que implica la utilización de algoritmos de redes neuronales y han comparado sus cálculos con las predicciones realizadas por el método de M&L obteniendo muy buenos resultados, sobre todo, en la fase ascendente del ciclo. ^{Marra, S. y Morabito, F. (2007}) describen una técnica basada en el algoritmo neural de Elman y también han mostrado resultados que mejoran los obtenidos por los métodos antes mencionados.

El CM es utilizado en el presente trabajo para predecir el comportamiento completo del ciclo solar número 24. Esto es debido a que es uno de los tres métodos utilizados por la SIDC y al cual se puede aplicar el filtro de Kalman (KF del inglés Kalman filter) descrito en el trabajo de ^{Podladchikova y Van Der Linden. (2011}) que permite mejorar las predicciones.

Materiales y métodos

Se ha realizado el registro de manchas solares con el telescopio Meade de 20, 3 cm de apertura y 2000 mm de distancia focal. Este registro ha sido posible gracias a la proyección de la imagen del sol sobre una pantalla acoplada al mismo. Las imágenes obtenidas fueron registradas en una hoja de papel con un círculo de 15 cm de diámetro impreso en él, donde se dibujaban detalladamente las manchas observadas. Posteriormente se determina el índice relativo de manchas solares usando la ecuación (1), además se procedió a clasificar las manchas y grupos de manchas, determinando sus respectivas coordenadas heliográficas utilizando para ello una carta solar, así como una plantilla heliográfica. Para determinar el factor de escala k se utilizó la siguiente relación:

Siendo Rm-i el valor promedio mensual observado, i meses antes del mes m en cuestión (i = 1, 2….6).

Con los valores promedios mensuales suavizados fue posible obtener la gráfica del índice mensual de manchas solares en función del tiempo (periodo 2007-2010).

^{Komitov et al. (2010}) determinaron la fecha del mínimo de actividad solar para noviembre de 2008 mediante el estudio del radio-índice F10.7 y el número internacional de manchas solares además de estimar la amplitud del ciclo 24 en 79±15 utilizando la regla de Waldemeier que relaciona el máximo del ciclo entrante y el promedio mensual de crecimiento de la actividad en la fase ascendente. ^{Hathaway y Wilson (2006}), encontraron la relación entre el máximo predicho para el ciclo que está por empezar Rmax y el valor promedio mensual del índice geomagnético interplanetario aaI para la fecha del mínimo mediante la ecuación:

Tabla 1 Valores del Índice Geomagnético Planetario (aaI) promedio para los meses finales del 2008 e inicios del 2009. 

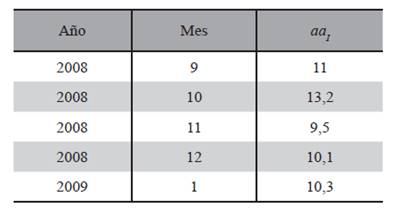
En la Tabla 1 se presentan los valores de aaI para finales del 2008. Se seleccionan los ciclos previos al 24 que tengan una amplitud de Rmax = 111, 95 ± 33, 9 de forma a contar con los ciclos anteriores con una amplitud entre los límites superior e inferior de este rango, siendo estos los ciclos 5, 6, 7, 12, 14 y 16 (Fig. 1).

^{Fessant et al. (1996}) han demostrado que se obtienen mejores resultados si se divide los ciclos en dos partes, y lo han aplicado para el método de redes neuronales. Siguiendo esa propuesta, pero en este caso para el CM, se ha dividido los ciclos en dos fases: una ascendente y otra descendente. Al existir una variación en la duración de los ciclos como se indica en la Tabla 2, un valor promedio ha sido utilizado y en casos de ciclos de menor duración que el promedio, se ha extrapolado los índices mediante la siguiente relación: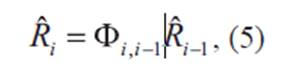

Donde R_i es el número de mancha solar suavizado extrapolado para el mes i en base a los valores originales del ciclo en cuestión, Ri?1 es el número de mancha solar suavizado para el mes i - 1 en base a los valores originales del mismo ciclo y Φi, i-1es la función de transición entre los meses i e i - 1.

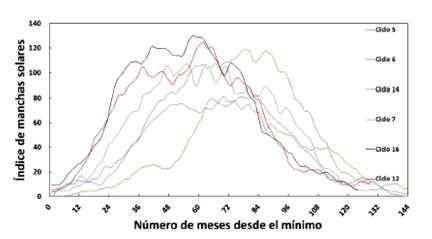
Figura 1: Ciclos 5, 6, 7, 12, 14 y 16, el ciclo 16 el de mayor amplitud, similar al ciclo 12, ambas con curvas bien diferenciadas de los demás, tanto en la parte ascendente como descendente. 

Este procedimiento es utilizado en la fase de extrapolación de la actividad solar en la aplicación del KF a cualquiera de los tres métodos anteriormente mencionados. Este proceso de filtrado se encuentra explicado detalladamente en Podladchicova et al. (2012) y se describe brevemente más adelante. Posteriormente en el CM se determina el promedio ponderado entre los ciclos en cuestión adjudicando diferentes pesos a cada uno de ellos.

Tabla 2.  Detalle de los ciclos utilizados para este estudio. SN*) Número de mancha solar (del inglés = Sunspot Number). 

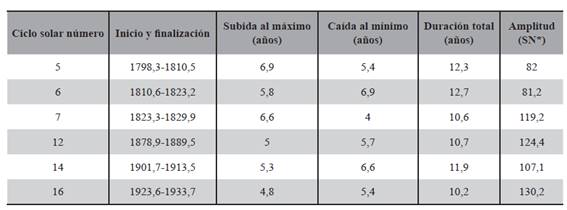
A cada ciclo le corresponde un peso dado por:

donde Rmax es el máximo predicho por la ecuación (4), siendo YMax el máximo del ciclo en cuestión.

Se procedió a determinar la suma entre los valores mensuales ponderados de los índices de manchas solares de los ciclos mencionados (Tabla 2) que se correspondan entre sí teniendo en cuenta en el número de meses desde el inicio del ciclo. De esta forma la suma de los valores promedios ponderados permite estimar la forma completa del ciclo venidero, en este caso la del ciclo solar N° 24.

Una vez obtenida la predicción completa del ciclo es posible aplicar el KF antes mencionado. Este método utiliza el siguiente algoritmo:

Extrapolación:

Donde: Rj j ?1 es el índice de manchas solares mensual suavizado extrapolado para el mes j.

Rj ?1 j ?1 es índice de manchas solares mensual suavizado extrapolado para el mes j - 1.

Aquí se utiliza el valor promedio suavizado del mes anterior que ha resultado de la aplicación del CM como punto de inicio.

δ² _j,j-1 es el error de varianza para la extrapolación del mes j - 1 al j.

δ² _j-1,j-1 es el error de varianza para la extrapolación del mes j - 1.

δ² _w,j es el error de varianza de proceso.

Filtrado:

Siendo Rm (j=1, 2, 3, 4, 5, 6) las últimas seis observaciones disponibles del promedio mensual del número de manchas solares.

Siendo Kj la ganancia de filtrado:

Para un error de varianza de la medida δ²v, j.

El procedimiento contempla la aplicación de un segundo filtro llamado de suavizado exponencial (ES del inglés Exponential Smoothing) de forma a reducir la componente estocástica introducida por la utilización de los últimos promedios mensuales de manchas solares en el proceso de filtrado. La relación utilizada es:

donde X k es el valor predicho tras la aplicación del ES para el mes k después del inicio del ciclo, X j k_1 promedio mensual suavizados para el mes k - 1, y X k predicción del KF para el mes k.

Las constantes de la ecuación (12) son elegidas con el peso exponencial α = 0,4 (0< α <1) de forma a tener una mejor respuesta para condiciones estándares del comportamiento de la actividad solar, pero con una menor calidad de filtrado para fluctuaciones aleatorias. El valor mensual suavizado del índice de manchas solares para octubre de 2008 fue utilizado como punto de inicio de la extrapolación para la fase ascendente del ciclo, para la fase descendente fue utilizado el valor correspondiente al mes de junio del 2014.

Resultados y discusión

En la Fig. 2 se puede apreciar el comportamiento diario del índice relativo de manchas solares correspondientes al observatorio FP-UNA calculadas por (1), usando k=1, comparadas con el índice relativo de manchas solares diario de la SISLO-SIDC, observándose una buena correspondencia entre ambos conjuntos de datos.

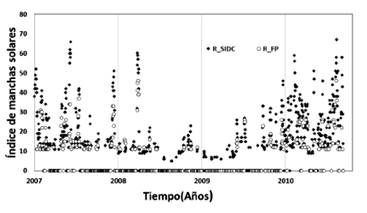
Figura 2: Comportamiento diario del índice relativo de manchas solares correspondientes al observatorio FP-UNA. Se observa una buena correspondencia entre ambos conjuntos de datos. 

Los valores promedio mensual del índice de manchas solares para el filtrado corresponden a los primeros seis meses, tanto en la parte ascendente como descendente del ciclo, en particular los meses de diciembre de 2008 a mayo de 2009 en el primer caso y de junio a noviembre de 2014 en el segundo, de esta forma la extrapolación se realiza para 62 meses en adelante para la fase ascendente y de 75 meses en la fase descendente.

Figura 3 Gráfica de dispersión para el cálculo del factor de escala (k = 1,46). 

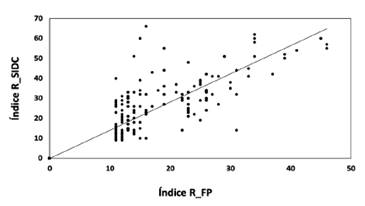
El factor de escala se determinó en k = 1,46 (Fig. 3), y los resultados anteriores permitieron ajustar los cálculos, notándose una mayor concordancia entre los números de manchas solares para valores más altos, observándose también un mínimo alrededor de noviembre del 2008 (Fig. 4).

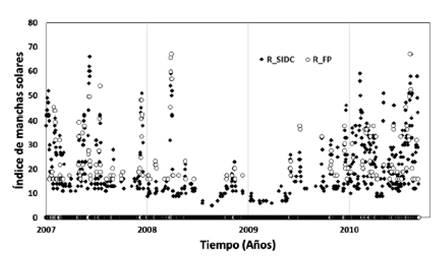
Figura 4 Comportamiento diario del índice relativo de manchas solares con cálculos ajustados. Se nota una mayor concordancia para valores más altos y un mínimo alrededor de noviembre del 2008. 

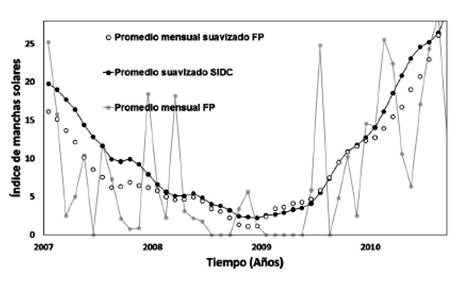
Utilizando los valores promedios suavizados fue posible observar el mínimo entre los ciclos 23-24 para noviembre del 2008 en concordancia con el estudio de ^{Komitov, B. et al. (2010}) mediante el estudio del radio-índice F10.7 y del número internacional de manchas solares. En la Fig. 5 se muestra el comportamiento de los valores mensuales promediados del índice de mancha solar comparados con los valores mensuales promediados del SISLO- SIDC, notándose una buena correspondencia entre ambas tendencias.

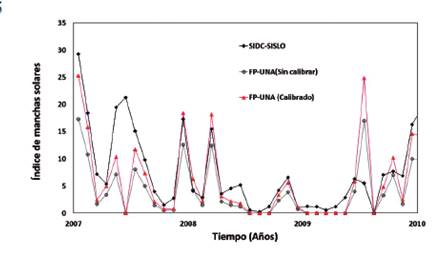
Figura 5 Comportamiento de los valores mensuales promediados del índice de mancha solar comparados con los valores mensuales promediados del SISLO-SIDC. 

La correspondencia entre ambas curvas es buena sobre todo en la parte ascendente como se observa en la Fig. 6. La amplitud predicha para el ciclo 24 es de 111, 95±13, 9 muestran un valor superior al calculado por Podladchicova y Van Der Linden. (2011) de 72 como límite máximo utilizando la relación entre la variabilidad de la velocidad de disminución de la actividad en la fase descendente con el máximo de actividad del próximo ciclo, sin embargo, se muestra más próximo a los 90, 7±9, 2 calculado por ^{Hamil y Galal. (2006)} mediante el estudio de los días sin manchas cerca del mínimo y aún más cerca de los 116, 4 observado según los registros de la World Data Centre (WDC) del Bureau of Meteorology of the Australian Government, Space Wheather Services (SWS).

Figura 6 Correspondencia entre las curvas promedio de los índices de manchas solares. 

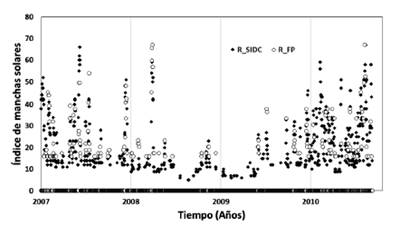
Figura 7 Predicción completa para el ciclo 24 mediante el CM. La correspondencia entre el ciclo observado y el predicho fueron mejorando mediante la aplicación de la división del ciclo en dos partes. 

El ciclo solar 24 está próximo a finalizar. ^{Rigozo et al. (2011}) estimaron la duración del ciclo en 11, 1 años basándose en la extrapolación de las componentes espectrales de los índices de manchas solares, el ciclo finalizaría en ese caso en diciembre de 2019. Se podría además tomar en cuenta los resultados de ^{Richards M.T. y Rogers M.L. (2009}) que sugieren un incremento en la duración de los ciclos durante las próximas décadas. El promedio de duración de 11, 4±1, 0 años fue utilizado como valor de referencia en el presente trabajo, se realizaron las predicciones hasta abril de 2020, mejorado mediante la aplicación de la división del ciclo en dos partes, disminuyendo el desfasaje muy notorio observado mediante la aplicación directa del CM (Fig. 7). En la Figura 8 se presentan la gráfica correspondiente luego de la aplicación de los dos filtros KF y ES.

Figura 8 Predicción completa para el ciclo 24. Se observa una mayor dispersión en los picos y una buena correspondencia en la parte monótona de la curva, tanto en la parte ascendente como la descendente, luego de la aplicación de los dos filtros KF y ES. 

Conclusiones

Se ha observado una buena relación entre la actividad solar registrada en el observatorio FP-UNA en el periodo 2007-2008 en comparación a los registros de la SISLO-SIDC. El mínimo de actividad solar entre los ciclos 23-24 fue calculado en noviembre de 2008. La predicción completa del ciclo 24 mediante la utilización del CM muestra un buen comportamiento en comparación al actual desarrollo de ciclo en cuestión sobre todo después de la aplicación de la división de los ciclos respectivos en dos fases y la posterior aplicación del KF y el ES, aún para una predicción en adelante de varias decenas de meses. Las predicciones decrecen en calidad a mediados de 2012 y fines de 2014 donde se ha observado dos picos de actividad muy pronunciados, esto es consecuente con las características del filtro aplicado.