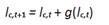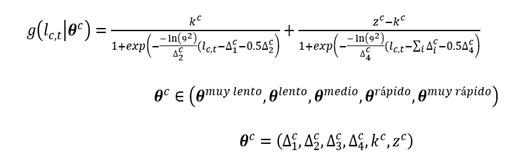INTRODUCCIÓN
Las proyecciones probabilísticas de población constituyen una de las temáticas demográficas que más desarrollos metodológicos han generado en los últimos años. Para construir una proyección de población es necesario proyectar primero sus componentes básicas: mortalidad, fecundidad y migraciones. Inevitablemente, todo pronóstico o proyección presenta una incertidumbre asociada, y esta puede informarse a través de distintas formas; variantes, escenarios, modelos probabilísticos o mediante la opinión de expertos. Cada una de estas propuestas para contemplar la incertidumbre da lugar a desarrollos metodológicos sustancialmente distintos. Frente a las proyecciones determinísticas clásicas, las nuevas propuestas probabilísticas ofrecen un rango de resultados posibles en lugar de las variantes habituales y además presentan una característica particular; la consistencia probabilística. Las agencias de estadística tradicionalmente se ocupan de la incertidumbre asociada al pronóstico de las variables demográficas produciendo dos o más pronósticos de fecundidad o mortalidad (o ambos), y luego calculando un rango de pronósticos. En la variante alta, se supone que la fecundidad es alta en todos los años del período de pronóstico. De manera similar, cuando la fecundidad es baja en un año, es 100% seguro que será baja en el siguiente año, también. Más aún, cuando se formulan dos o más variantes de mortalidad, además de las variantes de fecundidad, una variante de pronóstico con alto crecimiento poblacional resulta de combinar alta fecundidad con baja mortalidad (alta esperanza de vida), y viceversa para bajo crecimiento poblacional. Esto significa que, en la variante de alto crecimiento, cualquier año en el que la fecundidad es alta, la esperanza de vida también es alta. En otras palabras, se supone una correlación perfecta entre la fecundidad y la mortalidad, y una correlación serial perfecta para cada uno de los dos componentes. Suposiciones de este tipo son poco realistas y, además, causan inconsistencias: dos variantes que son extremas para una variable no tienen por qué serlo para otra variable.
Puntualmente, la mortalidad es la componente sobre la cual se han desarrollado la mayor cantidad de avances y propuestas, en parte debido a que es la componente que presenta mejor calidad y mayor disponibilidad en relación con las fuentes de datos y se trata del evento vital más simple de definir y registrar.
El contexto social, político y demográfico condiciona la investigación y cuando se habla de pronosticar la mortalidad o una de sus medidas derivadas; la esperanza de vida, se trabaja en un contexto mundial de debate sobre “envejecimiento” y se lo plantea como problemática. De acuerdo con Franco (2022) Pérez Díaz y Abellán García (2018), resulta “desafortunada” la expresión que se utiliza para referirse a este proceso demográfico, ya que crea una falsa analogía de naturaleza orgánica entre población y seres vivos. Sin embargo, las poblaciones no "envejecen" ni mueren. Por lo tanto, los cambios en la estructura de edad no significan que las estimaciones estereotipadas de la edad se transfieran a menudo a la población. Como señala Pérez Díaz (2018), es un término que “juzga el cambio poblacional como dañino antes de comprender sus causas y consecuencias”. Franco avanza y analiza que la cobertura mediática del "envejecimiento de la población" tiende a estar saturada de conceptos erróneos y estereotipos anticuados, acompañados de expresiones que presagian una "crisis demográfica" como un apocalipsis. Por lo general, se basan en suposiciones que resultan de interpretaciones parciales hechas con información incompleta o fragmentada. Por lo tanto, una perspectiva holística sobre el proceso demográfico actual es un enfoque tan necesario que tiene en cuenta factores tanto demográficos como no demográficos e incluso puede incluir una perspectiva transversal que incluya perspectivas de género, envejecimiento y antirracismo.
La tarea de pronosticar la esperanza de vida en la actualidad se enmarca en un contexto de crecimiento, desde 1960 hasta el año 2020, la cifra a nivel mundial aumentó de manera significativa, pasando de 46 a 69, mientras que la brecha entre los países menos desarrollados se ha reducido considerablemente (de 23 a 9 años). América Latina en particular ha logrado reducir la brecha con Argentina (de 11 a menos de 2 años) y ambos muestran tendencias futuras similares. La cifra para Argentina siempre ha sido alta en comparación con los países menos desarrollados y América Latina, y es ligeramente más bajo que los países desarrollados y lo seguirá siendo.
El presente trabajo desarrolla la estimación de la esperanza de vida al nacer para Argentina mediante un modelo probabilístico, el Modelo Jerárquico Bayesiano (MJB). A continuación, se realiza una breve revisión metodológica que permite situar el modelo en el contexto de desarrollo de las diversas propuestas probabilísticas.
Uno de los modelos precursores en el área y que de alguna manera abrió el camino a numerosas propuestas es el modelo que presentaron en 1992, Lee y Carter. Un modelo exigente con relación a la necesidad de datos. Este modelo actualmente cuenta con numerosas variantes y extensiones. Los autores proponen una metodología que permite modelar y extrapolar las tendencias observadas en las tasas de mortalidad y las medias a largo plazo. Este método se utilizó para predecir la mortalidad en los Estados Unidos hasta 2065. Avanzando sobre el modelo de Lee y Carter, Lee y Miller (2001) y Booth et al. (2002), introducen nuevas modificaciones; proble- matizan la elección del período de ajuste, el método para la estimación del parámetro de nivel y la elección de las tasas base para el pronóstico. La propuesta de los primeros autores es am- pliamente utilizada, sin embargo, la variante propuesta por Booth et al. (2002) ha demostrado ser al menos tan precisa como la de Lee y Miller en el corto plazo (Booth et al., 2005, Booth et al. 2006). Siguiendo el paradigma de datos funcionales, Hyndman y Ullah (2007) sugieren ajustar la mortalidad con regresiones spline penalizadas y luego ajustar un modelo usando descomposición de componentes principales. Estos métodos fueron desarrollados por Booth et al. (2006). Raftery et. al. (2013) proponen un enfoque que adapta la propuesta clásica de Naciones Unidas para proyectar poblaciones para todos los países del mundo, teniendo en cuenta que muchos de ellos tienen datos que son irregulares y de variable calidad. Los autores proyectan la esperanza de vida directamente, haciendo uso de un modelo de paseo aleatorio con una pendiente no constante. La pendiente es una función no lineal de la esperanza de vida actual y refleja el hecho de que la esperanza de vida tiende a mejorar más lentamente para los países con esperanzas de vida más bajas y altas, y más rápidamente para los países del medio. Raftery et. al. (2013) desarrollan entonces el modelo jerárquico bayesiano (MJB), que permite estimar la tasa de aumento en la esperanza de vida de un país utilizando datos anteriores de ese país, y también teniendo en cuenta los patrones pasados observados en todos los demás países. Luego Raftery (2014) usa el modelo de brecha femenina para desarrollar la esperanza de vida en varones. Finalmente, un nuevo método probabilístico que estima directamente la esperanza de vida de hombres y mujeres a cualquier edad es el método de Double GAP (Pascariu et. al, 2018) o Doble Brecha. El modelo de Doble Brecha realiza el pronóstico de la esperanza de vida femenina basado en el análisis de la brecha entre la esperanza de vida femenina en un país determinado, con el nivel máximo de esperanza de vida femenina a nivel mundial. Luego pronostica la esperanza de vida masculina analizando la brecha existente con la esperanza de vida femenina, reconociendo así de manera formal, la correlación entre la mortalidad de ambos sexos. De esta forma, el modelo se basa en el supuesto de que la esperanza de vida a lo largo del tiempo está altamente correlacionada entre países y entre hombres y mujeres.
El trabajo que aquí se desarrolla consiste en la aplicación crítica y el análisis de los resultados del Modelo Jerárquico Bayesiano, propuesto por Raftery, sobre la serie de tiempo de esperanza de vida mundiales con la finalidad de proyectar los valores de dicho indicador para la Argentina. A continuación, se contextualiza brevemente el indicador en estudio para la región y el país, luego se presenta en detalle la metodología estadística para luego avanzar sobre los resultados y culminar con las principales conclusiones.
La reducción de la mortalidad en la Argentina se inició más tempranamente que en la mayor parte de los países latinoamericanos y, a diferencia de estos, respondió, en sus comienzos, a mejoras en las condiciones generales de vida asociadas al desarrollo socioeconómico, más que al avance del conocimiento y la tecnología médica o a esfuerzos dirigidos a combatir directamente las enfermedades infecciosas (Lattes, 1975). Entre los factores que habrían contribuido al precoz inicio del descenso sostenido de la mortalidad, cabe mencionar la temprana modernización de la sociedad argentina en relación con la mayoría de los países latinoamericanos, su elevado nivel de urbanización y la expansión de la educación formal. Así, mientras que en la década de 1950 muchos países de la región se encontraban dando los primeros pasos en la transición epidemiológica, para ese entonces la Argentina ya había cubierto gran parte de su recorrido (Grushka, 2010). El mismo autor analiza la brecha entre sexos, la EVN de las mujeres es mayor que la de los hombres en el período en estudio. Si bien dicha diferencia era menor a un año en 1869-95, se da luego un aumento en la EVN que fue mayor para las mujeres, de manera que, siguiendo el patrón internacional, la sobremortalidad masculina se incrementa a medida que disminuye el nivel de la mortalidad general. A partir de 1970, las ganancias en la EVN en varones comienzan a aumentar y, por consiguiente, la sobremortalidad masculina comienza a decrecer y se estabiliza en las tres últimas décadas con una diferencia de alrededor de 7 años. En cuanto a la evolución futura de la mortalidad en la Argentina, las proyecciones oficiales más recientes publicadas por el Instituto Nacional de Estadística y Censos (INDEC, 2013) estiman que en 2040 la EVN sería de 78.4 años para varones y 84.7 para mujeres, con ganancias anuales decrecientes (Grushka, 2014).
MATERIALES Y MÉTODOS
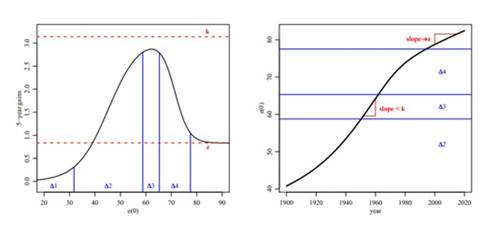
El MJB para la esperanza de vida desarrollado por Rartery et. al. Se basa en la metodología empleada en los últimos años por Naciones Unidas, sin embargo, este incluye la componente probabilística. Denotando con lc,t+1 la esperanza de vida al nacer, para el país, c, se proyecta para el próximo período de cinco años, t+1, que la esperanza de vida será la esperanza de vida en el período actual, lc,t , más las ganancias esperadas en la esperanza de vida, g( lc,t ). Si se analizan las ganancias observadas en cinco años en la esperanza de vida para 158 países desde 1950 hasta 2005 se destaca que no es constante la tasa de cambio. Para capturar esto, la ONU ha desarrollado modelos que representan las ganancias en la esperanza de vida por una doble función logística de la esperanza de vida actual. Los cinco modelos deterministas propuestos por la ONU varían entre ellos de acuerdo con el ritmo de aumento de la esperanza de vida.
La función logística doble tiene seis parámetros. Cuatro de ellos identifican intervalos de esperanza de vida cuando la tasa de ganancia en la esperanza de vida está cambiando, uno describe la ganancia máxima aproximada en la esperanza de vida, y el último parámetro da la tasa asintótica de ganancia a medida que aumenta la esperanza de vida. Para cada país, un analista de la ONU elige una de las cinco opciones prescritas de los seis parámetros evaluando el ritmo recientemente observado de disminución de la mortalidad (Naciones Unidas, 2022). El modelo implica que después de que la esperanza de vida alcanza cierto umbral, la esperanza de vida aumenta a un ritmo constante. Esto es consistente con la investigación que indica que no hay evidencia de un límite superior para la vida. expectativa (Oeppen & Vaupel, 2002).
La función logística doble (Meyer, 1994) es la suma de dos funciones logísticas de crecimiento de tres parámetros. La teoría de la transición demográfica sugiere que la esperanza de vida mejora lentamente al principio y luego más rápido a medida que un país entra en la transición demográfica. Las primeras ganancias rápidas son en gran parte como resultado de las mejoras en la mortalidad infantil y en la niñez. Una vez que la mayor parte de las posibles ganancias de se han logrado reducciones en la mortalidad infantil, los aumentos se ralentizan a medida que mejora la mortalidad cambio a edades más avanzadas. En resumen, la ONU proyecta la esperanza de vida en el próximo período de tiempo de forma determinista, usando la ecuación
El método de proyección de la ONU es determinista y no tiene en cuenta la incertidumbre, luego, el enfoque bayesiano lo convierte en un modelo estocásZtico para permitir la incertidumbre. Esto implica dos extensiones. Primero permite cambios estocásticos dentro de un país reempla- zando el modelo determinista (1) por uno estocástico añadiendo una perturbación aleatoria a (1). Luego se convierte en un paseo aleatorio con pendiente donde el término de la pendiente viene dado por la doble función logística. La segunda extensión es permitir que los parámetros de la doble función logística varíen entre países en un rango continuo en lugar de entre las cinco posibilidades actuales de la ONU.
RESULTADOS Y DISCUSIÓN
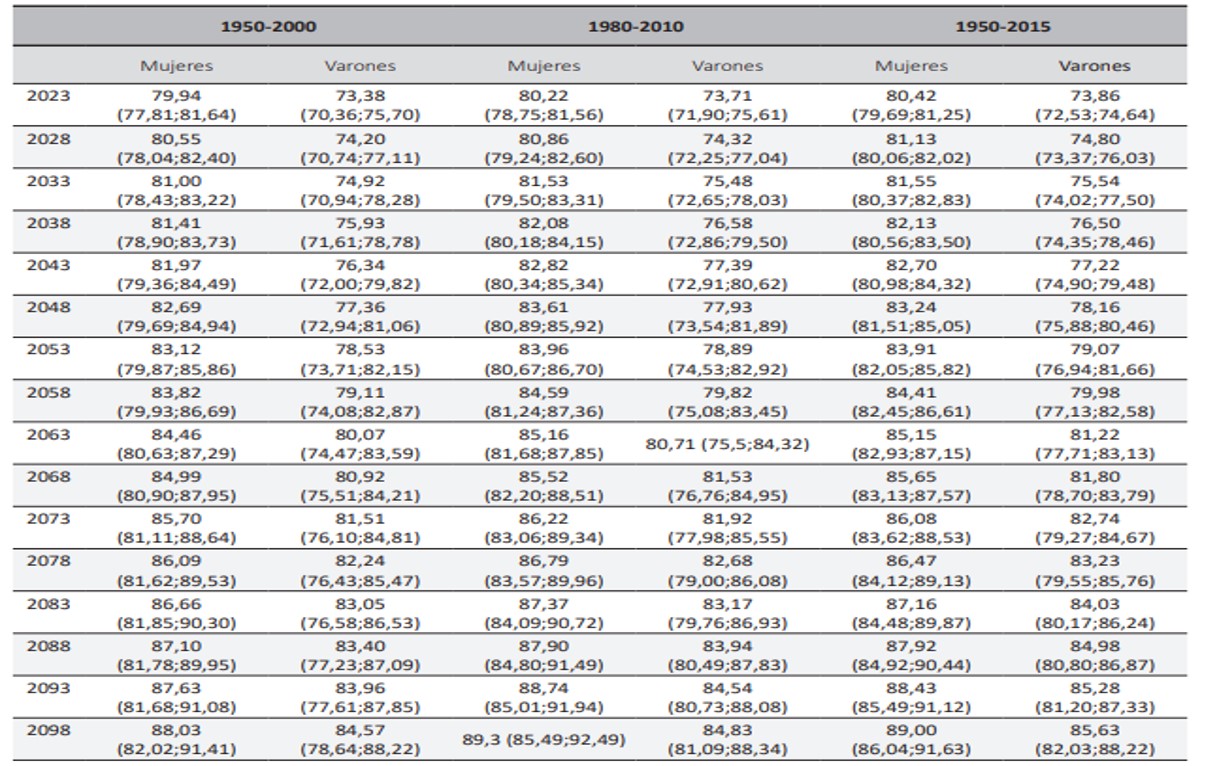
En este apartado se presentan los resultados obtenidos a partir de la estimación del MJB para los datos de esperanza de vida de Argentina. El modelo se calculó para tres períodos temporales seleccionados a partir de la calidad de los datos y la disponibilidad de una serie publicada por el organismo de estadísticas oficiales INDEC, disponible en WPP. En la Tabla 1 se observan los resultados para tres períodos seleccionados; 1950-2015, es decir la totalidad de los datos disponibles en WPP, 1980-2010; período para el cual la calidad del Sistema de Estadísticas Vitales esta evaluada y es recomendable su uso, y que, por otro lado, no incluye proyecciones de los denominadores (población). Finalmente, un tercer período: 1950-2000; que comienza a partir del primer dato disponible en WPP y finaliza antes de que las cifras incluidas en la serie estén calculadas a partir de los dos últimos censos; esta selección se realiza deliberadamente para evaluar el impacto de la tendencia previa a estos dos operativos versus la estimada a partir de los censos 2001 y 2010, relevamientos que presentaron grandes complejidades si se los compara con los realizados previamente. En al año 2001 se atravesó en Argentina una profunda crisis económica que impacto en varias formas sobre el operativo censal, por un lado, el descontento general de la población y por el otro la reducción salarial de los y las docentes que conformaban inicialmente la estructura censal, que fue reemplazada días previos al relevamiento. Si bien con el paso del tiempo los operativos censales han ido perdiendo adhesión por parte de la población, en el año 2010 ocurrió el fallecimiento del expresidente Néstor Kirchner, hecho que conmocionó a la población el mismo día en el que se estaba desarrollando el operativo, afectando el transcurso normal de la jornada.
Tabla 1: Esperanza de vida al nacer por sexo. Argentina. Período 2000-2095.
Fuente: elaboración propia.
Fuente: elaboración propia con base a INDEC.
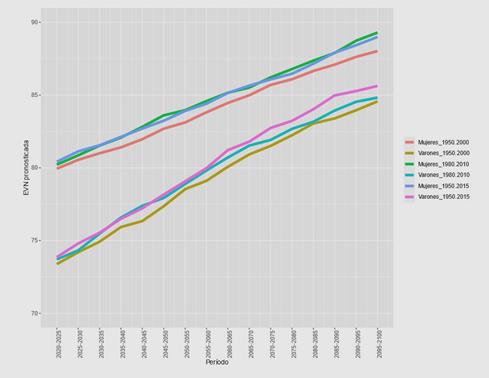
Figura 2. Esperanza de vida al nacer por sexo. Argentina. Período 2000-2095
En la Figura 2 se observan las series temporales de pronósticos de la EVN para varones y mujeres de acuerdo con distintos períodos de referencia para la modelización. Como primer resultado destacable las líneas que surgen de la modelización del período 1950-2000, tanto para varones como para mujeres, se ubican consistentemente por debajo de los restantes pronósticos. Es importante tener en cuenta que este escenario corresponde a una proyección en base a una tendencia histórica pero que no contempla en la construcción de las cifras base los censos 2001 y 2010. Es por ello que pensar el impacto sobre las esperanzas calculadas puede generar diversas hipótesis; el envejecimiento que aportarían a la estructura población los datos de los dos últimos censos disponibles a la fecha no se correspondería a una tendencia proyectada simplemente, sino que aportarían medio año extra de sobrevida a las estadísticas. Luego al comparar las otras dos propuestas; en mujeres no hay prácticamente divergencias, mientras que en varones los pronósticos se separan a medida que aumenta el horizonte de pronóstico. El escenario que incluye en el período base el último año disponible (2015) está por encima de los restantes, se alcanza una EVN de alrededor de 85 años y medio para el año 2100. Por su parte las mujeres alcanzan para ese año una esperanza de vida al nacer de 89 años. Sin embargo, en este punto, la elección del período base finalizado en 2010 o 2015 presenta una marcada diferencia para varones, con un año de diferencia en los pronósticos a largo plazo. Si bien se decide evaluar resultados en base al modelo oficial de UN, (período 1950-2015) este resultado podría introducir hipótesis acerca de la inclusión de proyecciones para calcular proyecciones y la obligación de repensar este aspecto en la propuesta oficial.
Luego se analiza la brecha entres sexos a partir del escenario obtenido en base al período 1950- 2015; la Figura 3. Muestra claramente como convergen las esperanzas de vida, con una desaceleración del aumento en mujeres y una aceleración en varones, llegando a ser la mitad de la brecha que se observa a principios del período. Resulta interesante evaluar estos resultados a la luz de los avances de las mujeres en la igualdad de oportunidades laborales, el acceso a puestos jerárquicos, el aumento en la participación del delito y por ende de la muerte por causas vio- lentas, etc. A su vez se observa una mayor amplitud de las bandas de confianza, en varones, a medida que avanza el horizonte de pronóstico.
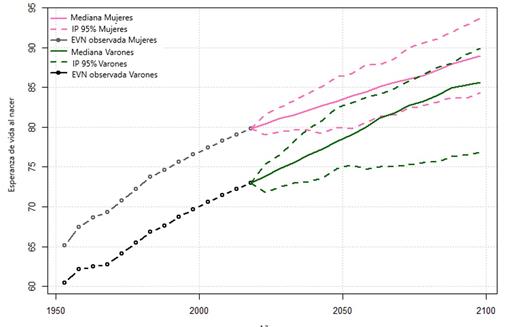
Fuente: elaboración propia con base a INDEC.
Figura 3. Esperanza de Vida al nacer observada y pronosticada, por sexo, Argentina. Periodo 1950-2095
Luego se presentan los pronósticos oficiales de INDEC a fin de realizar un análisis comparativo. El análisis pretende comparar la magnitud de las cifras obtenidas mediante la metodología de Naciones Unidas versus los resultados que el organismo nacional de estadísticas informa. La Tabla 2. presenta las EVN para mujeres y varones cada 5 años y hasta el 2040. Se destacan dos aspectos importantes, en primer lugar, la falta de un intervalo asociado a las estimaciones y, en segundo lugar, el limitado horizonte para el que se calculan las proyecciones, ambas limitaciones típicas de las proyecciones deterministas
Tabla 2: Esperanza de vida al nacer por sexo estimada y proyectada por INDEC, Argentina. Período 2000-2040.
| Años | Varones | Mujeres |
|---|---|---|
| 2000 | 70,04 | 77,54 |
| 2009 | 72,08 | 78,81 |
| 2015 | 73,72 | 80,33 |
| 2020 | 74,90 | 81,44 |
| 2025 | 75,96 | 82,42 |
| 2030 | 76,90 | 83,29 |
| 2035 | 77,72 | 84,05 |
| 2040 | 78,44 | 84,72 |
Fuente: INDEC. Estimaciones y proyecciones elaboradas en base al resultado del Censo Nacional de Población, Hogares y Viviendas 2010.
Para avanzar en la comparación se calcula la brecha entre sexos para ambas propuestas, la oficial de INDEC y la que el presente trabajo desarrolla; el Modelo Jerárquico Bayesiano. En la Figura 4. se presentan las brechas calculadas entre sexos en años. Claramente las proyecciones desarrolladas por INDEC presentan un descenso muy leve para una brecha que se sostiene en torno a los seis años para todo el período de pronóstico. Mientras que, por otro lado, el MJB proyecta una brecha en franco descenso que comienza en torno a los seis años y medio y termina en torno a los cinco años y medio para el año 2040.
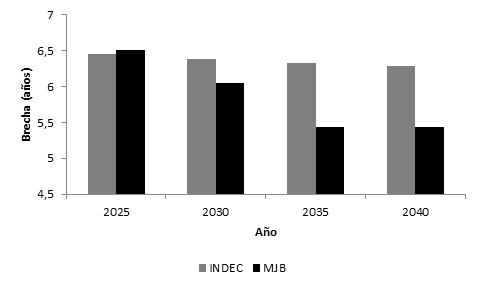
Fuente: elaboración propia con base a INDEC.
Figura 4. Brecha entre sexos en la Esperanza de vida al nacer proyectada por INDEC y el MJB. Argentina. Período 2025-2040
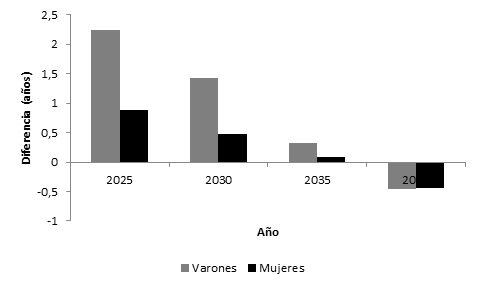
Finalmente, en la Figura 65, se analizan las diferencias entre ambas fuentes de pronósticos para cada sexo. Se observa una alta diferencia inicial, más alta en varones, siendo la misma de más de dos años, y de aproximadamente un año para mujeres. Luego las diferencias descienden y finalmente no exceden el medio año hacia el final del horizonte de pronóstico.
CONCLUSIONES
La teoría de la transición demográfica sugiere que la esperanza de vida mejora lentamente al principio y luego más rápido a medida que un país entra en la transición demográfica. En Argentina, a partir de 1970, las ganancias en la EVN en varones comienzan a aumentar y, por consiguiente, la sobremortalidad masculina comienza a decrecer y se estabiliza a partir de 1990 con una diferencia de alrededor de 7 años a favor de las mujeres. En cuanto a la evolución futura de la mortalidad en la Argentina, las proyecciones oficiales más recientes publicadas por el Instituto Nacional de Estadística y Censos estiman que en 2040 la EVN sería de 78.4 años para varones y 84.7 para mujeres, con ganancias anuales decrecientes.
Para obtener los pronósticos de la EVN mediante el MJB se proponen tres períodos temporales seleccionados a partir de la calidad de los datos y la disponibilidad de una serie publicada por el organismo de estadísticas oficiales INDEC, disponible en WPP; 1950-2000, 1980-2010 y 1950- 2015. Por su parte, en las proyecciones de INDEC se destacan dos aspectos importantes, en primer lugar, la falta de un intervalo asociado a las estimaciones y, en segundo lugar, el limitado horizonte para el que se calculan las proyecciones, ambas limitaciones típicas de las proyecciones deterministas.
Las brechas calculadas entre sexos en años comparando ambas fuentes presentan divergencias. Claramente las proyecciones desarrolladas por INDEC presentan un descenso muy leve para una brecha que se sostiene en torno a los seis años para todo el período de pronóstico. Mientras que, por otro lado, el MJB proyecta una brecha en franco descenso que comienza en torno a los seis años y medio y termina en torno a los cinco años y medio para el año 2040.
Si se comparan los resultados entre ambas fuentes se observa una alta diferencia inicial, más alta en varones, siendo la misma de más de dos años, y de aproximadamente un año para mujeres. Luego las diferencias descienden y finalmente no exceden el medio año hacia el final del horizonte de pronóstico.
El MJB presenta resultados plausibles junto con una medida de incertidumbre asociada que permite decidir hasta cuando serían confiables o informables lo pronósticos; en una primera inspección visual se observa una ampliación de los intervalos a partir de 1950, dicho año podría marcarse como un horizonte recomendable, sin embrago es en función del uso de las cifras obtenidas que podría decidirse un horizonte como informativo o no. Sin embargo, es importante tener en cuenta que el período base incluye proyecciones como datos de entrada, generando una paradoja de usar proyecciones para proyectar. La diferencia que se presenta en las proyecciones para varones da cuenta de la importancia en el modelo al incluir o no el último punto de la serie de datos. Si bien los modelos probabilísticos representan grandes avances quedan detalles por discutir, como el del período base y su relación con las fuentes oficiales (sean estimaciones o proyecciones).