INTRODUCCIÓN
Rodríguez Echenique (2018) afirma que la ciencia Bioquímica, y otras como Farmacología, Patología, son aprendidas en ecosistemas académicos formales como las aulas y los laboratorios. También afirma que las ciencias naturales puras suelen clasificarse químicas y físicas, y en ciencias de la vida y de la tierra y en el grupo de las ciencias aplicadas, se incluyen una variedad de campos que pueden abordarse como ciencias físicas aplicadas, incluyendo a la Aeronáutica, Electrónica, Ingeniería, Metalurgia o como ciencias biológicas aplicadas en las que se encuentran la Agronomía y Medicina.
Sin embargo, hay que tener presente, como lo expresa Rodríguez Echenique (2018) que los métodos y aun la misma noción de ciencia se van modificando con el tiempo y entre tantas metodologías se encuentran estrategias fundamentales que, excluyendo a las ciencias formales y sociales, y se hacen referencia solo a las ciencias naturales, como Biología, Química y Física en las cuales resultan obvias y esenciales la aplicación del método hipotético-deductivo y la Estadística.
Refiriéndose a los diferentes capítulos de la matemática pura, Bunge (2009) afirma que son racionales, sistemáticos y verificables, pero no objetivos, no brindan informaciones acerca de la realidad porque no se ocupan de los hechos, y que los entes ideales tanto los abstractos como los interpretados tratados en la Lógica y la Matemática, sólo existen en la mente humana y estas áreas del conocimiento, y son denominadas ciencias formales por ocuparse de inventar entes formales y de establecer relaciones entre ellos.
Algunos estudiosos han dividido las ciencias en duras y blandas; pero otros autores como Gil Antón (2004), creen que es necesaria revisar la posición actual que divide a las ciencias entre ciencias y “ciencias sociales”, o las caracteriza en duras y blandas. En este contexto, términos como “naturaleza de las ciencias”, “naturaleza de la biología”, “naturaleza de la química” o “naturaleza de la física” son oídos en los ámbitos académicos. ¿Difieren, pues, ciencias como la biología, bioquímica, física, geología, matemáticas, en las principales características de su naturaleza? Intuitivamente podría pensarse que las características de las diversas ciencias son diferentes, pero apenas se ha investigado sobre este asunto (Acevedo Díaz, 2008).
En tal sentido, Galicia et al., (2001) han destacado que, para el aprendizaje de las matemáticas en ciencias químico-biológicas, es importante y primordial, el modelado de experimentos. Así la caracterización y deconstrucción de la práctica proporcionan elementos importantes para experimentación en el laboratorio, de modo a mostrar las concepciones de los estudiantes del funcionamiento de las entidades matemáticas, las relaciones logarítmicas, la linealidad de la velocidad de desaparición de reactivos respecto a las diferencias de estos, la interpolación lineal y la primera aproximación de la serie de Taylor, contando con conocimientos de química y matemáticas. Los estudiantes al predecir asocian el modelo con lo modelado, actividad distintiva de los investigadores.
Galicia et al. (2001) han referido que en ciertas subespecialidades de la bioquímica una de las prácticas relevantes es el seguimiento de cinéticas, mostrando algunas evidencias de que la práctica social constituye el motor de la evolución profesional al acercar la caracterización de la práctica, de modo que la experimentación y el empleo de modelos tiende a concebir la actividad escolar cercana de su actividad cotidiana, en donde la experiencia se impone a todo cálculo matemático.
Para Hernández et al. (1993), en estos tiempos, la Inteligencia Artificial es un nuevo paradigma para la representación del conocimiento, en la cual la Lógica Matemática constituye la base teórica, permitiendo que en Biología y Neurofisiología y por extensión en Bioquímica se pueden realizar variados modelados. Se presentan algunas conceptualizaciones de Bioquímica y de Matemática, para delimitar y contextualizar dichos términos, a la luz de diversos autores.
Mora Guevara et al. (2018) expresan que “la matemática como ciencia formal se encarga del estudio, análisis, relaciones y propiedades de entidades abstractas como son los números, símbolos y figuras geométricas, haciendo uso del razonamiento lógico; en fin, es una ciencia que se interrelaciona con otras ciencias como disciplina y a su vez se divide en dos ramas, como lo son las matemáticas puras y las matemáticas aplicadas”.
Por su parte, Nelson et al. (2001), enuncian que la bioquímica trata de explicar la vida en términos químicos unificadores, señalando que disciplinas aparentemente sin relación con la bioquímica pueden responder importantes preguntas de la bioquímica, coincidentemente con Martínez-Vaz (2014) que resalta el carácter interdisciplinario de la bioquímica, y que considerada como materia o asignatura presenta un reto para la enseñanza efectiva. Otras conceptualizaciones de Bioquímica son dadas por Murray et al. (2012), que consideran a la bioquímica como la ciencia de la base química de la vida; mientras que Roskoski (1998) la define como una ciencia médica y biológica imprescindible para comprender la biología celular.
El objetivo de la bioquímica es conocer y comprender los eventos que permiten un adecuado funcionamiento de los seres vivos, y los fundamentos para entender la alteración de estos procesos. La bioquímica no está aislada, forma parte de un grupo de disciplinas que interactúan para la total comprensión del organismo humano (Maldonado-Frías, 2013). En cuanto a cuestiones epistemológicas de las Matemáticas Duval (1998) plantea como paradoja:
“. . . estamos entonces en presencia de lo que se podría llamar la paradoja cognitiva del pensamiento matemático: por un lado, la aprehensión de los objetos matemáticos no puede ser otra cosa que una aprehensión conceptual y, por otro lado, solamente por medio de las representaciones semióticas es posible una actividad sobre los objetos matemáticos” (p. 175).
Flores-Espejo (2020), en su investigación sobre la construcción reflexiva de enunciados epistemológicos en el laboratorio de bioquímica, recomienda orientar la construcción de enunciados epistemológicos hacia aspectos específicos de la investigación científica como la experimentación o los datos e incluir el modelo didáctico que le permita a los estudiantes la construcción reflexiva de la concepción de la naturaleza de las ciencias más acorde con las doctrinas filosóficas actuales.
En el Paraguay, la Agencia Nacional de Evaluación y Acreditación de la Educación Superior (ANEAES), creada por ley N° 2072 del año 2003, ha caracterizado a la carrera de Bioquímica en las siguientes áreas de formación: Ciclo de formación básico o inicial, Ciclo de formación biomédica/pre profesional, Ciclo de formación profesional, Ciencias sociales y humanidades/ciclo de formación complementario, Pasantía supervisada y Trabajo de grado (Agencia Nacional de Evaluación y Acreditación de la Educación Superior [ANEAES], 2013). Se han encontrado publicaciones científicas de la relación de las matemáticas con otras especialidades de la química, como los aportes de Caicedo et al. (2000), que refieren que las matemáticas han estado incorporadas en las mallas curriculares de ingeniería química desde sus comienzos y establecen una relación sinérgica entre las matemáticas y la ingeniería química. Sin embargo, resultan escasas o casi inexistentes las publicaciones que focalizan la relación o presencia de las matemáticas en los pensums de las carreras de Bioquímica.
Por el motivo anteriormente expuesto se desarrolla esta investigación, con el propósito de estudiar las áreas y contenidos de las matemáticas empleadas en la enseñanza de las asignaturas que integran las mallas curriculares de las carreras de Bioquímica en el Paraguay.
METODOLOGÍA
La investigación se basó en un enfoque cualitativo, transversal y descriptivo. Se realizó un análisis documental de las mallas curriculares de las carreras de Bioquímica (una universidad de gestión pública y cuatro privadas) acreditadas por la ANEAES en el Modelo Nacional socializadas en la página web oficial de la ANEAES más dos programas de las asignaturas de dos carreras de Bioquímica, uno por cada tipología de gestión mediante autorizaciones solicitadas a las instituciones.
En el análisis de los programas fueron considerados todas las asignaturas, sean obligatorias u optativas, y realizando una matriz de consistencia con cuatro apartados (área de formación, operaciones matemáticas, área de la matemática y asignatura) atendiendo las unidades y contenidos declarados en los sílabos y a la luz de los contenidos hallados en la bibliografía básica. Además, fueron registradas las herramientas matemáticas necesarias para la resolución de problemas, comprensión o interpretación de contenidos en el año 2022.
RESULTADOS
Después de haber analizado cinco mallas curriculares y dos programas de las asignaturas de dos carreras de Bioquímica se obtiene los siguientes resultados:
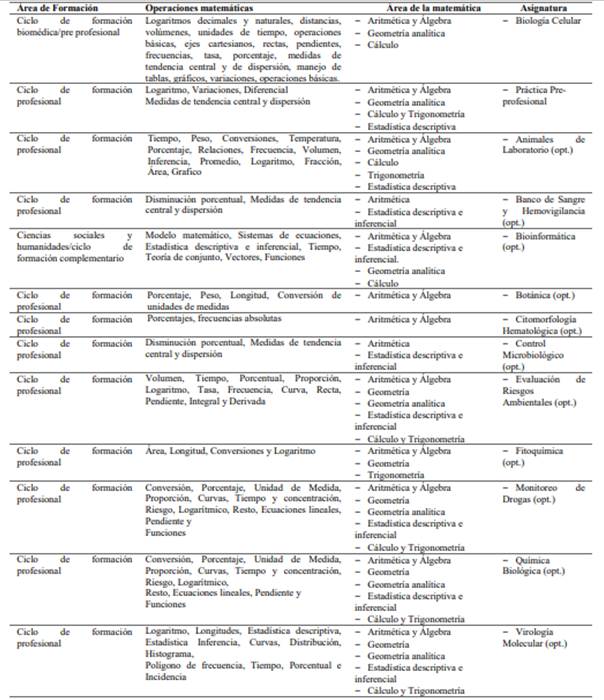
En la tabla 1 se muestra entre áreas de formación de la Bioquímica, operaciones matemáticas fundamentales para cada disciplina y el área de la matemática a la cual corresponde, es decir, asignaturas que contienen cálculos cuantitativos relacionadas con las diversas áreas de formación de la carrera de Bioquímica. Se percibe que la aritmética, álgebra, geometría analítica y estadística se encuentran en las cuatro áreas de formación (inicial, pre profesional, profesional y complementario).
Tabla 1. Relación entre Bioquímica y Matemática (contenidos mínimos por asignatura del plan de estudios, Criterios de calidad para la carrera de Bioquímica de la ANEAES, 2013)
Fuente: Elaboración propia con base al Modelo Nacional de Mecanismo de Evaluación y Acreditación de carreras de grado de la carrera de Bioquímica de la ANEAES.
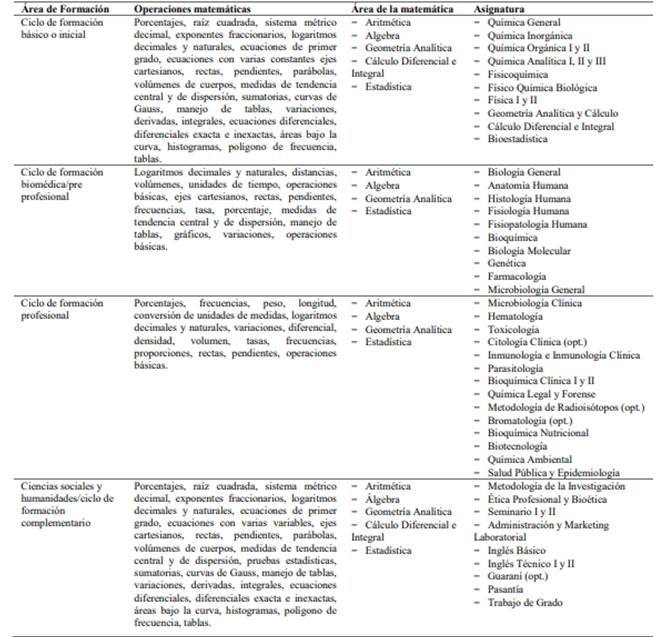
En la Tabla 2 se contempla algunas asignaturas específicas ofertadas en forma diferenciada por alguna de las carreras y, su relación con los contenidos y áreas específicas de la matemática. Asimismo, la aritmética, álgebra, geometría analítica y cálculo se encuentran como base en la formación pre profesional, profesional y complementario de las carreras universitarias.
DISCUSIÓN
La matemática es necesaria para la comprensión de cualquier fenómeno, formando parte de la construcción de las ciencias. Las ciencias son creaciones humanas; y para la interpretación de ellas en su completa dimensión e inclusive para que muchas puedan existir es menester el lenguaje del universo que es la matemática. Sin embargo, la relación matemática-ciencias muchas veces está prácticamente ausente en la enseñanza, o bien sus conocimientos se transmiten de forma aislada, sin mostrar su cultura y utilidad; pero si se encara la matemática desde una pedagogía integral e integradora la misma contribuye en un proceso educativo transdisciplinar que muestra el concierto de fantasías que entrelazan todas las ciencias, en mayor o menor intensidad (Rodríguez, 2011).
Dicho esto, en primer lugar, se destaca que todas las asignaturas contempladas en el Modelo Nacional de Mecanismo de Evaluación y Acreditación de carreras de grado de la ANEAES están incluidas en las mallas curriculares de las carreras de Bioquímica acreditadas.
Así se denota, que todas las áreas de formación en la carrera de Bioquímica están relacionadas directa o indirectamente con alguna área de las matemáticas, siendo comunes a todos los ciclos de formación la aritmética y el álgebra, aunque las operaciones matemáticas realizadas varíen de una disciplina a otra.
Por otro parte, en el ciclo de formación básico o inicial es donde más variedad de operaciones matemáticas se realizan, lo cual va en coherencia con el tipo de asignaturas desarrolladas, tales como las fisicoquímicas y las diversas químicas analíticas, aplicando sobre todo los conceptos y en resoluciones de problemas, temáticas centrales de geometría analítica y cálculo, por lo que se suscribe por completo las reflexiones de Galicia et al., (2001) en cuanto a la importancia de la caracterización y deconstrucción de la práctica de modo a proporcionar elementos importantes para experimentación en el laboratorio o salón de clase, de manera a mostrar las concepciones de los estudiantes del funcionamiento de las entidades matemáticas.
En el caso del idioma guaraní, que forma parte del ciclo de las ciencias sociales y humanidades /ciclo de formación complementario, la relación con las matemáticas se establece utilizando el guaraní como instrumento didáctico, de conformidad con la competencia requerida para la formación del futuro bioquímico, cumpliendo con la ley 4251 (2010). Este mismo empleo puede extenderse al idioma inglés en las asignaturas de inglés básico e inglés técnico I y II.
En cuanto a metodología de la investigación, las disciplinas matemáticas más empleadas están relacionadas a las pruebas de hipótesis, desarrolladas en estadística inferencial, al igual que las medidas de tendencia central y de dispersión desarrollados en estadística descriptiva. En cuanto al trabajo de grado, herramientas fundamentales son la estadística y bioestadística, con posibilidad de aplicación de cualquier disciplina matemática, lo que va en total armonía con la metodología de las ciencias naturales que es hipotética-deductiva, en total consonancia con Gutman & Castro (2003) que han considerado que en la aplicación y la extensión de la Matemática a la Química, resulta principalmente interesante, las formas en que las estructuras y los métodos matemáticos existentes pueden ser aplicados adecuadamente a la Química y a su vez en la Bioquímica.
Entre los hallazgos recurrentes de operaciones matemáticas sobresalen las conversiones del sistema métrico decimal, aplicaciones de área y volumen de cuerpos, ecuaciones de rectas, de geometría analítica tienen también muchas aplicaciones las hipérbolas, parábolas, sigmoideas y otras figuras. Todos estos hallazgos denotan coincidencias con Campbell y Farrell (2009), que describen a la bioquímica como un campo del saber que se apoya en muchas disciplinas, y cuya naturaleza multidisciplinaria le permite usar resultados de muchas ciencias para ofrecer respuestas a interrogantes acerca de la naturaleza molecular de los procesos o transformaciones vitales.
A lo largo de toda la malla curricular de la carrera de Bioquímica se encuentra presente la matemática, por lo que en total sintonía con lo descripto por Caicedo et al. (2000) que describe la relación entre las matemáticas y la ingeniería química como sinérgica; la presente investigación extiende esa relación sinérgica y cooperativa a las matemáticas con la bioquímica.
Se concluye que los resultados demuestran la presencia de las diversas áreas de las matemáticas en las mallas curriculares de las carreras de Bioquímica de universidades paraguayas. Se aplican la aritmética, el álgebra, geometría plana, del espacio y la analítica, el cálculo diferencial e integral, la estadística, entre otros.
Aplicaciones de las matemáticas se observan en la enzimología, que constituye un capítulo fundamental de la Bioquímica, dedicada al estudio de las enzimas, desarrollan una cinética característica, expresada mediante la ecuación de Michaelis-Menten. Esta expresión matemática básica y fundamental en bioquímica como lo expresan López Nicolás y García Carmona (2015) permite la descripción del cambio experimentado por la velocidad de una reacción catalizada enzimáticamente al cambiar la concentración del sustrato, asumiendo que se establece reacción entre la enzima y su sustrato, y la formación de un complejo entre la enzima y el sustrato, hipótesis comprobada experimentalmente medio siglo posterior del establecimiento de la ecuación, mediante técnicas espectroscópicas.
La matematización de la química puede extenderse a la bioquímica, así se tiene que el álgebra computacional puede ser aplicado en forma de herramientas para estudiar redes bioquímicas, como el realizado por Pérez Millán (2011), encontrando invariantes que se satisfacen en los estados de equilibrio, posteriormente el abordaje de sistemas cuyos estados de equilibrio se describen por binomios y son denominados sistemas con estados de equilibrio teóricos, mostrando mecanismos enzimáticos de fosforilaciones secuenciales distributivas con sus características, e incorporando resultados computacionales para estados de equilibrio positivos, desde la perspectiva de la geometría algebraica real y finalmente, presentar un modelo discreto del módulo de regulación del factor nuclear NF-κB, por medio de un sistema polinomial dinámico discreto. Este enfoque permite estudiar redes cuya información disponible es poco detallada, con la idea de proveer una primera descripción, siguiendo con lo expresado por Pérez Millán (2011).
Todos estos hallazgos dan el estatus de ciencia interdisciplinar y transdisciplinar a la bioquímica en cuanto a su relación con la matemática. Finalmente se puede concluir que la bioquímica como ciencia que estudia la vida a nivel molecular y como carrera universitaria, está matematizada.