Estimado editor:

Las investigaciones en ciencias de la salud enfocadas en el análisis de las fuentes de evidencias de validez en instrumentos psicométricos, son importantes para una adecuada inferencia e interpretación de la medición de un test. En este contexto, es importante la evaluación de la consistencia interna para la propiedad de la puntuación del test en un determinado grupo. En los últimos años, existe más información para conocer las limitaciones, supuestos y estimación de diversos coeficientes que evalúan la consistencia interna. Recientemente se demostró que, la estimación bayesiana de coeficientes de confiabilidad coincidió con las estimaciones frecuentistas y el rendimiento mejoró cuando el tamaño de la muestra aumentaba¹. El enfoque bayesiano permite realizar interpretaciones intuitivas de la incertidumbre en su inferencia, obtener intervalos de credibilidad y utilizar la distribución posterior para responder preguntas de confiabilidad, lo cual no se podría realizar desde un análisis frecuentista.

Los próximos estudios psicométricos publicados en la revista, podrían considerar una estimación más intuitiva sobre la confiabilidad y realizar preguntas relevantes sobre su inferencia². Para esto, proporcionamos un tutorial en Rstudio para estimar la confiabilidad bayesiana en medidas unidimensionales a través del coeficiente omega bayesiano (ω). La base de datos y script se puede encontrar en el repositorio OSF (https://osf.io/wapbt/?view_only=) y corresponde a una escala de cinco ítems que presenta un formato de respuesta Likert.

Realizamos la instalación, luego cargamos los paquetes y la data:

# instalación de paquetes

install.packages(c("remotes", "haven", "coda", "pacman"))

library(remotes)

remotes::install_github("juliuspfadt/Bayesrel")

# cargando paquetes y base de datos

library(pacman)

p_load(haven, Bayesrel, coda)

data <- read_sav("ifis.sav")

Establecemos una semilla para la replicabilidad con set.seed, aunque la distribución posterior puede variar ligeramente cuando se vuelve a ejecutar. La confiabilidad bayesiana se obtiene con la función strel y los resultados se resumen con summary. Podrá observar otros valores de coeficientes, aunque en nuestro ejemplo nos enfocamos en el coeficiente ω, cuya interpretación es la siguiente: “La media posterior para el coeficiente ω es igual a 0,786 (intervalo de credibilidad del 95 %: 0,749, 0,818) y existe un 95 % de probabilidad de que el coeficiente ω se encuentre en el intervalo de 0,749 y 0,818.”

set.seed(25)

# ------ coeficiente omega bayesiano ------ #

coef_bayesiano <- strel(data = data, freq = FALSE)

summary(coef_bayesiano)

Results:

point est 95 % CI lower 95 % CI upper

Bayes_alpha 0,78808 0,75363 0,82029

Bayes_lambda2 0,79319 0,75995 0,82622

Bayes_glb 0,82211 0,79178 0,85478

Bayes_omega 0,78617 0,74938 0,81883

La distribución posterior del coeficiente ω, se puede utilizar para realizar preguntas sobre la confiabilidad del test. Mediante la función pStrel, podemos preguntar: ¿Cuál es la probabilidad de que la confiabilidad sea mayor que 0,78? y ¿Cuál es la probabilidad de que la confiabilidad se encuentre en el intervalo de 0,70 y 0,90? La interpretación para la primera pregunta: “Los datos han aumentado la probabilidad de que el coeficiente ω exceda el límite de estimación 0,78 de 0,078 (probabilidad previa) a 0,650 (probabilidad posterior).” Para la segunda pregunta: “Los datos han aumentado la probabilidad de que el coeficiente ω se encuentre en el intervalo 0,70 - 0,90 de 0,134 (probabilidad previa) a 1 (probabilidad posterior).”

# ¿Cuál es la probabilidad de que la confiabilidad sea mayor que 0,78?

pStrel(x = coef_bayesiano, estimate = "omega", low.bound = 0,78)

Results:

prior_prob posterior_prob

0,07813928 0,65087719

# ¿Cuál es la probabilidad de que la confiabilidad se encuentre en el intervalo de 0,70 y 0,90?

pStrel(x = coef_bayesiano, estimate = "omega", 0,70) -

pStrel(x = coef_bayesiano, estimate = "omega", 0,90)

Results:

prior_prob posterior_prob

0,1341203 1,0000000

Para evaluar si el muestreo Monte Carlo de la cadena de Markov (MCMC) ha convergido a la distribución posterior del coeficiente ω, se puede utilizar el estadístico R-hat, el cual debe ser inferior a 1,1. En nuestros resultados, el R-hat presentó un valor de 1,00168 y graficamos las muestras de MCMC con la función traceplot (Figura 1, sección A).

# ------- diagnóstico de convergencia ------- #

samp <- coef_bayesiano((Bayes))(("samp"))(("Bayes_omega"))

# restructuración de las cadenas para traceplot:

samp_list <- as.mcmc.list(lapply(as.data.frame(t(samp)), mcmc))

traceplot(samp_list, col = c("skyblue", "magenta", "blue"),

main = "Diagnóstico de convergencia", xlab = "Iteraciones")

# índice R-hat

gelman.diag(samp_list)$psrf(, 1)

Results:

point est.

1,00168

Por otro lado, mediante un análisis post-hoc de la verificación predictiva posterior (PPC) podemos analizar el modelo factorial unidimensional del coeficiente ω. La Figura 1, sección B, permite observar la matriz de covarianza de los datos (puntos negros) y los intervalos del 95 % (barras grises). Los puntos negros se encuentran dentro de los intervalos y esto sugiere la unidimensionalidad. Para reforzar esta interpretación, se pueden obtener índices de ajuste bayesianos^3,4. El modelo mostró un buen ajuste con medianas posteriores aceptables para el BRMSEA = 0,047 [HPD del 90 %: 0,00, 0,08] p = 0,897, BSRMR = 0,024 y BLR = 10,33.

# ------- Comprobación predictiva posterior (PPC) ------- #

omegaFit(data = data, coef_bayesiano)

Results:

$Bayes

$Bayes$LR

(1) 10,33004

$Bayes$srmr

(1) 0,02440296

$Bayes$rmsea

(1) 0,04742891

$Bayes$rmsea_ci

Lower upper

0,0000000 0,0804188

$Bayes$p_rmsea

(1) 0,897193

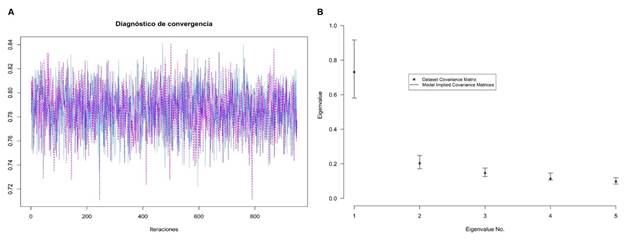
Figura 1 A. Traceplot de la convergencia del MCMC para el coeficiente ω. B. Verificación predictiva posterior del ajuste unidimensional 

Por último, se podría analizar la confiabilidad para cada ítem mediante el siguiente código: coef_omega_item <- strel(data = data, estimates = c("omega"), item.dropped = TRUE, freq = FALSE), y resumir con summary(coef_omega_item). Esperamos que la presente contribución sea de utilidad para los investigadores aplicados que realizan el análisis de la confiabilidad en instrumentos psicométricos unidimensionales.