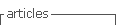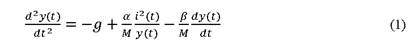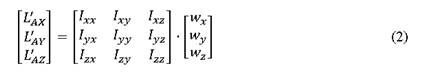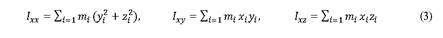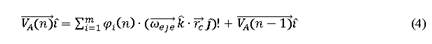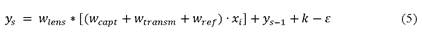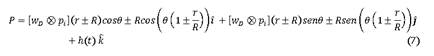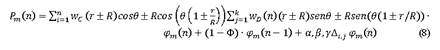INTRODUCCIÓN

Las energías renovables (ERNC) se perfilan como una solución en el control de emisiones contaminantes al medio ambiente. A partir de los objetivos de desarrollo sostenible para América Latina, se evidencia la necesidad de reducir los residuos tecnológicos resultantes de la etapa de desmantelamiento de las turbinas eólicas, a fin de minimizar el impacto ambiental de las ERNC.

Actualmente, en el diseño de sistemas de energías renovables es fundamental el compromiso por restablecer las condiciones ambientales a su equilibrio natural, por lo que es necesaria la formulación de modelos matemáticos para mitigar los efectos del gradiente de presión y temperatura, aguas abajo del parque eólico, mediante filtros y generadores de micro vórtices (MVGs) de compensación. Lo que se puede lograr a través de conceptos de un parque eólico flexibles, wind kite reconfigurables con tecnología origami, configuración eólica tándem (topología de capas de cometas con función de lentes eólicas), alineación de arreglos tipo clúster de captadores distribuido, con inteligencia de enjambre de partículas y optimización colaborativa, para el ajuste dinámico de parámetros.

El mantenimiento regenerativo de los sistemas eólicos instalados actualmente requiere minimizar el reemplazo frecuente de elementos móviles, por lo que se plantea disminuir el número de componentes a través de un optimizador centralizado, que se traduce en un menor número de componentes residuales. Para ellos es necesario establecer un algoritmo de alineación de ángulos YPR (Yaw, Pitch, Roll), en relación con la posición relativa del arreglo eólico, para seguimiento del punto de máxima potencia, así como el control de pérdidas en mecanismos de transmisión, todo esto a fin de maximizar la eficiencia energética y sustentar el modelo circular, extender la vida útil de la infraestructura instalada y diseñar etapas de actualización del sistema por software, a través de lenguaje descriptor de hardware VHDL, donde el peso de la optimización está en el modelo matemático y algoritmos de control del arreglo reconfigurable.

De esta manera, se plantea un codificador de flujo eólico con arquitectura basado en registros desplazamiento con realimentación lineal - LFSR, para la compensación por MVG, recirculación de flujo eólico y recuperación de energía potencial del sistema, con el objetivo de obtener mínimo impacto ambiental sobre el entorno, en el marco del concepto de sistemas eólicos inteligentes. Un reto corresponde al cálculo del ángulo relativo entre los elementos del grupo, donde se debe concatenar la ecuación de trayectoria de la curva cíclica en el modelo de control adaptativo. De modo gráfico se pueden solapar o superponer las trayectorias proyectadas en el plano horizontal π_H, plano vertical π_V y plano proyectado de control del ángulo de inclinación del plano.

Fractales de Vibración en patrones simétricos.

Para la optimización de la captación de energías renovables, por recirculación de flujo de energía del movimiento ondulatorio, se analiza la técnica de modelado basada en patrones simétricos entre las cometas, considerando las ondas estacionarias por reflexión de flujo (fenómeno entre dos ondas superpuestas de igual frecuencia y amplitud, pero en direcciones opuestas). Esto crea un patrón estacionario en el que ciertos puntos de la onda parecen estar en reposo, mientras que otros puntos experimentan un movimiento vibratorio, que se evidencia con la formación de patrones geométricos, con zonas de máxima y mínima vibración, para determinación de frecuencias naturales de estructuras, estos principios pueden ser aplicados en la corrección de efectos de difracción de los captadores sobre el flujo eólico, a fin de mitigar los efectos de las turbinas eólicas sobre la fauna y el entorno de los espacios intervenidos.

Estos conceptos se requieren del desarrollo de nuevas tecnologías, donde se plantea una red tecnológica para el desarrollo sostenible de la región de América Latina, basados en laboratorios móviles de estudio de parques eólicos e investigación I+D, sobre el modelo matemático interpretado (bloques discretos de energía y registro en cámaras de aire entre captadores), que permita la configuración dinámica, reutilización de componentes, mantenimiento regenerativo en sitio, actualización tecnológica y optimización sobre soporte de hardware reconfigurable, sobre un estudio de interpretación de las etapas de conversión, el diseño conceptual presentado en la Figura 1 (mapa eólico: Itaipu, 2016), con la descripción en VHDL de los criterios del algoritmo.

Figura 1.  Diseño Conceptual del Laboratorios de Cometas Eólicas. 

Las zonas de potencial eólico por regiones, permite establecer un mapa de ruta para el laboratorio móvil, en un sistema eólico portátil, compuesto de un arreglo de cometas eólicas (optimizadoras - captadoras), con configuración definida por software, basado en una estación base colectora de energía cinética móvil, elementos captadores basados en estructuras tensadas, un algoritmo de alineación de ángulos YPR del arreglo dinámico y un esquema de mantenimiento en función de la tecnología de los materiales, control de flujo activo y la trayectoria descrita por el conjunto, todo esto con el propósito de disminuir el impacto ambiental, en todas las etapas del proyecto.

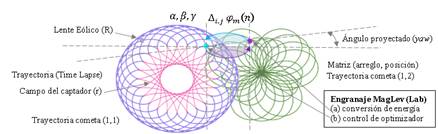
Para sincronizar la proyección sobre los captadores y las trayectorias dinámicas del arreglo de captadores, dado por el arreglo de cometas eólicas, se plantea el control de posición de las cuerdas de accionamiento, por levitación magnética (MagLev), así como tensores y componentes magnéticos entre las cometas, con el objetivo de mantener la relación de distancia óptima entre los elementos. Esta solución permite disminuir el costo energético del esquema de control, minimizar pérdidas en la transmisión mecánica y disminuir las necesidades de mantenimiento del mecanismo de engranajes del proyector de trayectoria del arreglo de cometas, basados en engranajes planetarios, donde la órbita de los elementos se proyecta en el espacio de control de flujo de energía.

En esta oportunidad se platea el control vectorial como una herramienta de interpretación de los coeficientes de optimización para definir los parámetros de posición sobre los ejes xyz, a fin de configurar la altura del proyector y establecer un arreglo dinámico de cometas captadoras, con el objetivo de cubrir una superficie extendida del parque fotovoltaica, de forma eficiente. Esto mediante la combinación del modelo matemático del sistema de captación de energías renovables (Sandoval-Ruiz, 2021).

Antecedentes

Recientes investigaciones analizan el efecto del control de ángulos (Yang et al., 2022) estima los factores ambientales en el ajuste del ángulo yaw, (Palacios et al., 2023) presenta un control de ángulo pitch y (López el al., 2023) realizó un análisis numérico de torque en turbinas con modificaciones denominadas generadores de vórtice (VGs), bio-inspirados en las plumas del halcón peregrino, mediante el uso de simulación computacional de la dinámica de fluidos (CFD) en 3D, lograron validar el aumento el porcentaje de producción energética de los aerogeneradores, al generar vórtices turbulentos de baja intensidad que evitan el desprendimiento de la capa limite ante cambios bruscos de dirección del viento entrante. El efecto de estela (wake turbulence) generado en la energía con grandes fluctuaciones de amplitud por las turbinas eólicas, representan una alta carga dinámica sobre los aerogeneradores ubicados corriente abajo del arreglo o parque eólico. Por lo tanto, la comprensión de la dinámica de la estela turbulenta y el desarrollo de modelos de ingeniería para una predicción rápida de su evolución aguas abajo son esenciales para el avance de las tecnologías eólicas, este tema es abordado a detalle en (Zhang et al., 2023) donde se explica la dinámica de la estela cercana y lejana sobre el flujo eólico, proponiendo una fórmula empírica para describir sus variaciones a favor del viento en diferentes posiciones de la envergadura de los captadores, ampliamente tratado en (Vahidi et al., 2022). Lo cual es insumo para la determinación del modelo de control adaptativo de los ángulos de entrada y salida, en la trayectoria de desplazamiento del captador a través de una secuencia de corrimiento coordinado de manera colaborativa, a fin de cancelar el efecto y mejorar la eficiencia e impacto sobre el entorno.

Así mismo, se ha encontrado que una alineación específica del ángulo de guiñada (yaw) de las turbinas eólicas en un parque eólico mejora la producción de energía promedio del arreglo eólico (^{Dou et al., 2020}), los resultados indican que la optimización del ángulo de guiñada mejora la potencia de un parque eólico inteligente hasta en un 7 % en tiempo real, en respuesta a los cambios en la dirección del viento entrante. Todos estos datos experimentales (Rivarolo et al., 2020), (Li at al., 2021), (Ozbay et al., 2021). muestran que las características de la estela ante diferentes ángulos de guiñada que se superponen entre sí, cuando se alinean correctamente, permite optimizaciones a través de expresiones analíticas de modelos dinámicos basados en la física.

Los estudios computacionales mediante el uso del método de volúmenes finitos, modelos de energía cinética turbulenta k-ε y ecuaciones de conservación de la cantidad de movimiento lineal sobre flujos con coeficientes viscosidad dinámica (^{González & Hinojosa, 2019}), representan un insumo para la definición de parámetros del control adaptativo del flujo eólico, relación mecánica-geométrica de los álabes del rotor y coeficientes resultantes del algoritmo LMS. La ecuación de acoplamiento por levitación magnética para este sistema en eje y de movimiento está dada por (1):

Donde y(t) es la distancia entre el imán acoplado y el electroimán de control (el cual puede ser sustituido por fluido ferromagnético), i(t) es la corriente que fluye por el electroimán de control, M es la masa del imán de acoplamiento al eje del captador eólico, y g es la constante gravitacional. El parámetro β es el coeficiente de fricción por viscosidad del aire (este es determinado por el medio donde se mueve el imán de acoplamiento), y α es una constante de fuerza de campo que está determinada por el número de vueltas de alambre en el electroimán y la fuerza del imán. Para la relación de coeficientes LMS-geométricos, con proporcionalidad establecida entre las componentes del momento cinético (L) y de la velocidad angular (ω) se establece mediante un tensor de inercia (2).

Siendo los componentes del tensor de inercia (I): los momentos de inercia y productos de inercia, coeficientes de las componentes de la velocidad angular (3).

Se puede establecer un tensor de inercia adaptativo por geometría, por masa variable, a través de la configuración de las cometas captadoras por control electromecánico de la estructura, micro-tabs, configuración magneto-elástica de osciladores acoplados.

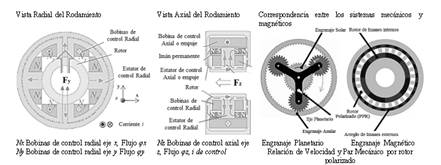
Acoplamientos en Transmisión y Soportes de Levitación Magnética del eje de la Cometa Eólica

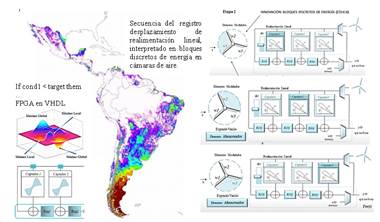
En consideración a la resistencia mecánica por fricción en el eje de acoplamiento del arreglo de cometas de captación de energías renovables, se han considerado alternativas de soportes de MagLev (Vizcaino, 2019), (Wu et al., 2010), de control magnético para posicionamiento del eje de transmisión, ya que la ausencia de fricción y mínima amortiguación permite optimizar los modelos de transmisión magnéticos (Figura 2). En el caso de los engranes magnéticos el movimiento se transmite por la atracción y repulsión de los imanes que están en la periferia de los discos, en (Primero et al., 2017) se describe el modelo matemático detallado del reductor de velocidad cicloidal.

Figura 2.  Control de transmisión y rodamientos de Levitación Magnética (Primero et al., 2017).  

Estos modelos requieren la optimización de parámetros geométricos mediante el análisis FEM, análisis dinámico del sistema y control de posición axial, a fin de alcanzar una levitación estable y eficiencia en la rotación. En (Mansi et al., 2021) se aplican estimadores de mezcla y regresores dinámicos - DREM. Donde los parámetros de posición del eje y velocidad del rotor estarán ponderados por el flujo magnético variable, definido por el control de corriente en la bobina de accionamiento.

Interpretación de Control Vectorial aplicado a accionamientos magnéticos por Curvas Cíclicas

La variable del sistema de transmisión magnética para el posicionamiento del arreglo de cometas inteligentes, puede ser manejada como un vector rotando, si se considera este vector en un marco de referencia que también está rotando con una velocidad angular, a la frecuencia síncrona de la curva cíclica de barrido de la proyección sobre la superficie en el plano del accionamiento, siendo una de las variables de control el flujo magnético en el engranaje de acoplamiento, según la relación vectorial (4).

Se desarrolló la ecuación de relación del vector de velocidad en la transmisión con un componente de flujo magnético dinámico 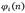, que pondera la relación de la velocidad lineal, definida en relación de la velocidad angular y el radio desde el borde del engranaje al eje de transmisión.

MATERIALES Y MÉTODOS

Caso de Estudio. Modelado LFSR-ANN de convertidores eólicos comerciales de las siguientes características: Diámetro 116.00 m y Potencia 5000 KW (para velocidad de viento > 12 m/s y densidad de aire referencia de 1.225 Kg/m3). Datos de la ubicación seleccionada para el ensayo: Densidad de aire (ρ) 1.21 Kg/m3 y rango de velocidad de viento de 2.50 a 8.60 m/s. Se establece el modelado teórico del sistema eólico, considerando coeficientes de un arreglo centralizado de seguimiento y control de sobre la matriz eólica instalada, de donde se obtiene (5).

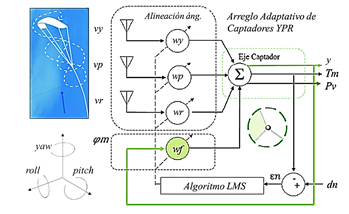
Del estudio de potencial de las fuentes de energías renovables en un punto específico, se analizan las condiciones de la región, en la adaptación en sitio se requiere la triangulación de datos para establecer los criterios de optimización, con recirculación de flujo incidente (sobre un ángulo de entrada). La definición de la arquitectura del arreglo optimizador para el sistema, como combinador lineal con realimentación (Figura 3), para la descripción del modelo en hardware.

Figura 3.  Arquitectura del Combinador Lineal Adaptativo. 

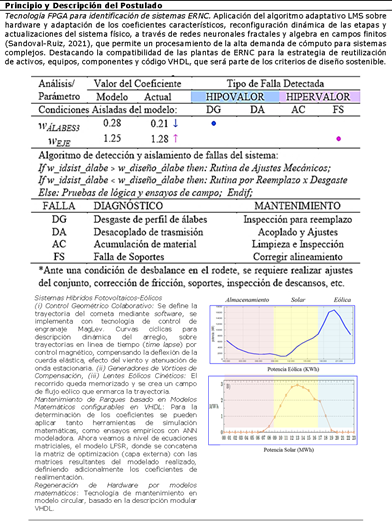
La descripción del algoritmo adaptativo en VHDL permite definir el comportamiento de los coeficientes de optimización del modelo (Sandoval-Ruiz, 2020), sobre un filtro adaptativo LFSR, mediante el método de optimización de la función de costo el algoritmo de descenso por gradiente.

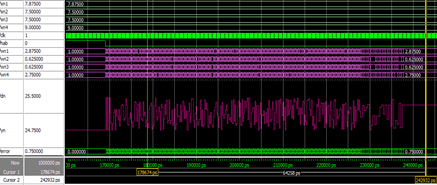
Se simuló el modelo teórico para un punto de operación, donde se plantea obtener el mínimo error global, al valor target establecido. En la Figura 4 se puede observar que el algoritmo LMS converge en aproximadamente 800 ns. con un error promedio de 0.75.

Figura 4.  Resultados de Simulación del Algoritmo Adaptativo LMS-AH. 

Finalmente, se plantea la extrapolación de datos estadísticos del modelo para compensación de impacto ambiental, mediante la interpretación de los coeficientes matemáticos (wi) y accionamiento de posición del cometa, mediante ensayos empíricos sobre trayectorias cíclicas, a fin de correlacionar los ángulos YPR óptimos.

ANÁLISIS DE RESULTADOS

Se realizó una aproximación práctica para 10 a 12 cometas eólicas 2.1 MW x 10 aprox. 25.5 MW. Los descriptores matemáticos de registros desplazamientos con realimentación lineal, se han seleccionado para el modelado de los sistemas, aplicando ecuaciones geométricas sobre el modelo para el filtrado de componentes. En los laboratorios móviles de muestreo de zonas de potencial eólico (ver Sandoval, 2021 para revisiones de los conceptos relacionados), se plantea el cambio de variable del estudio teórico para el ensayo empírico de ajuste del ángulo de alineación, a través de la configuración de parámetros de mecánica de fluidos. El coeficiente wn4 de realimentación, ha sido asociado con la recirculación de flujo sobre el ángulo de guiñada, como flujo reflejado de otros captadores del arreglo, este parámetro se desgloza y se obtiene mayor controlabilidad del sistema, así como la simplificación por método empírico de compensación de estela en la configuración de trayectorias geométricas del parque eólico.

El diseño biomimético (Sandoval-Ruiz, 2023) permite el control óptimo (Sandoval et al., 2008) de tensión de las cuerdas¹, coeficientes magneto elásticos, sintonización de frecuencia de resonancia paramétrica eólica y la matriz del tensor de inercia, ajustados sobre los coeficientes del modelo en función de la distancia entre elementos (6), en base a los ángulos α,β,γ de incidencia sobre cada eje, así como las fuerzas empuje y sustentación del arreglo.

Donde el radio o distancia r _j de los elementos del arreglo es inversamente proporcional al cuadrado o en su forma interpretada, factorial de la distancia relativa, por lo que este término se anula para grandes distancias donde el efecto de la difracción, diferencial de presión, patrón de flujo de la estela de cada captador, son despreciables en función de las variables directas del modelo.

El análisis por etapas permitió simplificar el modelo del arreglo optimizador, incorporando un descriptor dinámico, que se corresponde con la trayectoria de barrido de los elementos del arreglo en configuración planetaria, donde los orbitales descritos establecen la relación de los elementos, para lograr una realimentación de energía en proporción Fibonacci² se tendrá una relación entre los radios del arreglo de las curvas cíclicas. De esta forma, se busca identificar el sistema en tiempo real, formular los lentes ópticos por dinámica del arreglo y desarrollar un sistema eólico cognitivo, con el propósito de minimizar los componentes hardware, por procesamiento neuronal. También se pueden considerar la resonancia paramétrica (^{Brandenberger, 2023}) para captación piezoeléctrica y mejoras continuas de mitigación del impacto ambiental. Del análisis teórico se puede obtener como resultado una ecuación modeladora (7) del arreglo optimizador.

Donde ^W _D corresponde al coeficiente de difracción del arreglo, que superpone los aportes de las cometas de concentración y proyección, la operación de convolución

, que comprende el producto algebraico de los componentes directos (incidentes), más el aporte de la realimentación (reflejada) del patrón de flujo de energía p _i , estimado para la posición dinámica de la trayectoria compuesta entre los elementos del arreglo. La ecuación puede ser reescrita desarrollando la operación de convolución concatenada para el lente concentrador ^W _D y lente de difracción, de la forma expresada en (8).

Donde n,k serán los índices del LFSR, en este caso se están haciendo coincidir con los parámetros geométricos de las curvas cíclicas, donde definen el número de lazos, orbitas o espines en la trayectoria del arreglo optimizador. Se logró reducir la complejidad del sistema de control y optimización, mediante la incorporación de componentes en la formulación del arreglo geométrico, que comparado con estimadores de redes neuronales permite un manejo de variables directo sobre la interpretación del sistema, respecto a redes recurrentes y NARX (Matlab, 2023) para control de accionamientos de transmisión MagLev.

Figura 5. Trayectorias configurables para Cometas Eólicas. 

CONCLUSIONES

Gracias al análisis de compensación, se incluyó al término de realimentación la alineación respecto a trayectoria en el modelo de sistemas eólicos regenerativos, con capacidad de adaptación de parámetros, brindando soporte para la actualización y reconfiguración de sistemas de energía renovables. El reto de ingeniería se ha logrado superar al establecer un modelo dinámico para las plantas actuales, orientado a la configuración dinámica, basado en principios de reutilización y sostenibilidad.

De esta manera, se logró un compromiso con los recursos ambientales y los ecosistemas, a partir de la generalización del modelo para nuevas tecnologías, tal es el caso de cometas eólicas (Sandoval-Ruiz, 2023), dado que se desarrolló un estudio de transferencia de energía a fin de aislar las etapas de forma independiente para la conversión en la estación del laboratorio móvil, siendo el modelo compatible para una dinámica según la función de optimización específica.

Incorpora la descripción de arreglos de cometas de optimización compatibles para fotovoltaica (Sandoval-Ruiz, 2020) y eólica, extrapolables a inspección y mantenimiento, aplicando una selección de variables físicas y geométricas de la trayectoria del optimizador móvil, para asistencia de las tecnologías instaladas y obtener la configuración óptima para el sistema, a través de técnicas como de redes neuronales fractales con geometría circular y nodos en capas radiales.

Otro factor diferenciador de la propuesta corresponde a los ciclos de captación, a través de elementos pasivos y seguimiento de los puntos de máxima potencia por concentradores eólicos activo, accionados por engranajes MagLev. En el tema de sostenibilidad se plantea la reutilización de equipos e infraestructura de la capacidad instalada, en adaptaciones a nuevas tecnologías, la aplicación de circuitos acoplados, para disminuir la modificación de patrones de flujo en interacción con la biosfera (Sandoval-Ruiz, 2021) y la remediación del impacto ambiental de estas tecnologías.

Se plantean postulados (Tabla I) para un mecanismo de optimización del arreglo de captadores de energías renovables, según las características de potencial y condiciones ambientales, sobre un presupuesto de potencia, basado en la capacidad, excedente de energía para su almacenamiento y costo energético de sistemas activos (consumo de los módulos), como parámetros de la función objetivo en la minimización de pérdidas y efectos sobre las variables mecánicas y térmicas, de energía residual.

Tabla 1.  Postulados y Propuestas de Trabajos Futuros.