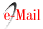INTRODUCCIÓN
El subdimensionamiento o sobredimensionamiento de una obra implica costos excesivos a lo largo del tiempo; por lo tanto un proyecto intermedio sería la solución ideal, generando los menores costos anuales. Los resultados podrían ser confiables siempre que existan suficientes datos disponibles y no hayan ocurrido modificaciones importantes en el régimen de lluvias durante el período de registro, o después; se acepta entonces, la condición de que el comportamiento del sistema continuará siendo el mismo durante el período de cálculo (en el futuro). Los estudios hidrológicos constituyen una herramienta básica para establecer hasta qué punto es factible y seguro un proyecto de desarrollo hidráulico, dentro de una cuenca o microcuenca hidrográfica. La selección correcta de una avenida de proyecto constituye un aporte esencial de los estudios de ingeniería, para prevenir y controlar los problemas mencionados, es importante tener un criterio técnico muy amplio en el estudio hidrológico del potencial de avenidas. Para ello, es necesario disponer de información de series de precipitaciones máximas de mayor longitud de registro, esta nos permitirá interpretar el comportamiento hidrológico de un evento, con el propósito de predecir el riesgo que puede sufrir los proyectos de mayor envergadura y garantizar la vida económica de estructuras hidráulicas.
En la región Moquegua, la ocurrencia año tras año de eventos máximos de precipitación o máximas avenidas, causan problemas hidrológicos, como inundaciones dentro de las partes bajas de la cuenca, destrucción de obras hidráulicas viales dentro de la cuenca, los deterioros a los suelos por erosión, riesgo de vida útil de las obras de canalización y transporte de sedimentos, debido al exceso de lluvias en los meses de Enero, Febrero, y Marzo. Los daños que causan las avenidas, son notorios en el aspecto económico y social en las comunidades de la región, con mayor incidencia en las actividades agrícolas, pecuarias y urbanas. El diseño de muchas de las obras para protección frente a eventos máximos, requiere de la estimación del caudal máximo a través del empleo de probabilidades obtenidas desde registros históricos. Pero en el caso de no contar con registros de caudal, este debe estimarse a partir de la precipitación, y en este caso de la precipitación máxima. Es por ello que es necesario plantear modelos regionales para precipitaciones máximas, de modo que se pueda estimar con mayor precisión para cada lugar dentro de la región Moquegua. La razón fundamental de investigación es estudiar el efecto de las variables geográficas en las precipitaciones máximas de 24 horas en la región. La utilidad de los resultados es estimar las precipitaciones máximas de 24 horas en cualquier lugar de la región Moquegua con las relaciones regionales determinadas, que es muy útil para los cálculos de diseño para estructuras viales como alcantarillas, las cuales se presentan en muchas partes dentro de la región, también servirá para estimar las precipitaciones máximas que ingresan a modelos precipitación escorrentía muy utilizados para estimar la erosión.
En la estadística existe decenas de funciones de distribución de probabilidad teóricas; de hecho, existen tantas como se quiera, y obviamente no es posible probarlas todas para un problema particular. Por lo tanto, es necesario escoger, de esas funciones, las que se adapten mejor al problema bajo análisis (Aparicio, 2010). Entre las funciones de distribución de probabilidad usadas en hidrología se tiene las siguientes: Normal, Lognormal, Pearson III, Gumbel, Funciones para dos poblaciones. Las funciones anteriores, aun cuando son las más comúnmente usadas en la hidrología aplicada, no son todas (Aparicio, 2010). Es muy importante la existencia de registros pluviométricos para estimar crecientes de diseño y sugieren realizar análisis regional de frecuencias con precipitaciones máximas diarias anuales (Bolainas Castillo et al., 2011).
El análisis de la precipitación diaria es un tema de gran interés, puesto que las precipitaciones torrenciales son uno de los mayores riesgos ambientales, así se ha investigado la concentración temporal a esta escala de tiempo (Benhamrouche & Martín Vide, 2011). La magnitud y la frecuencia de precipitación es de gran importancia en el diseño en hidrología e hidráulica, pero la disponibilidad de datos de precipitación están limitados a pocas zonas donde se ha instalado estaciones meteorológicas exitosamente y eficientemente, por ello en zonas sin estaciones la precipitación puede evaluarse por agrupar zonas con características similares (Ahuja & Dhanya, 2012). Se desarrolló una formula empírica IDF (intensidad duración frecuencia) para estimar la intensidad de precipitación para cualquier duración y para cualquier período de retorno con mínimo esfuerzo, para ello se han utilizado datos de precipitación diaria (Rashid et al., 2013).
Se ha desarrollado herramientas útiles para calcular la precipitación e intensidad de lluvia para cortas duraciones utilizando registros de precipitaciones máximas de 24 horas y ajustes a ecuaciones encontradas en la literatura previa (González & Mora, 2013). Se ha revisado el patrón de distribución temporal de varias tormentas en la costa de Chiapas, en especial las tormentas de 24 y 6 horas de duración, se tuvo como referencia el patrón de tormenta del SCS (servicio de conservación de suelos) tipo III de Estados Unidos, que es un patrón propuesto para zonas costeras (Morales-Hernández et al., 2014).
Además otra investigación evaluó la magnitud de la precipitación para diferentes períodos de retorno y también acertaron el tipo de distribución de probabilidad que mejor se ajuste a los datos de precipitación de Dharamshala, India. Utilizaron 20 años de datos de precipitación anual útil para la predicción de precipitación máxima de un día en un año, y la precipitación máxima de dos a siete días consecutivos, variando el período de retorno de 2 a 20 años (Kumar Sharma & Kumar, 2016). Así mismo se realizó el análisis de frecuencia de datos de precipitación máxima diaria del distrito de Udaipur, utilizaron además: 56 años de datos, 07 distribuciones de probabilidad diferentes y la prueba de bondad de ajuste Chi cuadrado (Baghel et al., 2019).
Los productos satelitales de precipitación se han utilizado para la advertencia temprana de deslizamientos de tierra, productos como las imágenes TRMM, para determinar umbrales y la predicción de lluvia para utilizarse en la advertencia temprana de estos desastres (Chikalamo et al., 2020). Existen varios factores que afectan los eventos de lluvias extremas en el Pacífico Sur en diferentes escalas de tiempo. Para ello se ha utilizado datos de precipitación diaria. Se agrupo estaciones pluviométricas en clústeres (Pariyar et al., 2020). La lluvia diaria extrema se ha intensificado y se ha vuelto más frecuente a nivel global. Comúnmente los índices usados que examinan las características de la lluvia raramente muestran cambios históricos a largo plazo estadísticamente significativos en eventos de lluvia medios y extremos (Dey et al., 2020).
El entendimiento de la distribución espacio-temporal de las características de la lluvia tiene un rol mayor en la evaluación de la disponibilidad de los recursos hídricos sobre una cuenca. Por consiguiente, es necesario entender los cambios en las características usando datos de precipitación grillados y análisis estadísticos robustos para tomar decisiones (Venkata Rao et al., 2020). Los datos de precipitación son una entrada meteorológica vital para sistemas de modelamiento agrícolas y estudios de planeamiento y gestión de recursos hídricos. Datos fueron usados para investigar la variabilidad espacio temporal de la precipitación. Para estudios de variabilidad de la precipitación el índice de variabilidad de precipitación, el índice de concentración de la precipitación y un modelo de regresión lineal, fueron empleados (Animashaun et al., 2020).
Los métodos estadísticos se apoyan en la existencia de series de datos en el lugar de interés, los cuales son sometidos a un análisis de frecuencias usando técnicas tradicionales de estudio. Esto implica que la curva de frecuencia definida para un determinado lugar es válida rigurosamente para ese lugar; cuando generalmente la información que se requiere es en un lugar diferente, donde no existen datos medidos; la regionalización de datos permite combinar informaciones de diversos lugares en la cuenca o región, para producir por ejemplo, una curva regional de frecuencias, válida en toda la región y lugares sin información; este recurso entre tanto, está limitado a descargas de hasta 100 años de período de retorno.
En forma general la regionalización permite conocer la precipitación máxima de forma distribuida y por tanto es un aporte para estudios hidrológicos diversos. El estudio también es una base para la adecuación y el ordenamiento territorial de la región, y permitirá la elaboración de planes, programas y proyectos sostenibles en relación a los riesgos frente a eventos extremos de lluvia. Una investigación aplico el método de L-momentos para regionalización de precipitación máxima diaria en Golestán en el noreste de Irán (Malekinezhad & Zare-Garizi, 2014). Otra investigación clasificó el estado de Kerala en un número óptimo de zonas homogéneas basado en la precipitación mensual. Utilizaron el método de clúster de Ward tomando datos de precipitación mensual para cinco años consecutivos del 2008 al 2012 de 63 estaciones pluviométricas (Shahana Shirin & Thomas, 2016). Se realizó la regionalización obteniendo regiones homogéneas utilizando las pruebas de Fisher, de L-momentos y de discordancia, previamente realizaron pruebas de homogeneidad e independencia, su estudio lo realizaron en Chiapas, México (Aguilar Suarez et al., 2017). También se realizó regionalización de precipitación en la cuenca del río Guayas en Ecuador, estudiaron además la agresividad y la concentración de la lluvia. Utilizaron los índices de Fournier y de concentración de precipitación para describir la distribución en espacio y tiempo. Además ellos, utilizaron datos mensuales y determinaron regiones homogéneas mediante el método k-means (Ilbay-Yupa et al., 2019).
Las preguntas formuladas fueron: ¿Qué relación existe entre las precipitaciones máximas de 24 horas con los factores geográficos en la región Moquegua?, ¿Cuál es la función de distribución probabilística regional adecuada para las precipitaciones máximas de 24 horas en la región Moquegua? La hipótesis general fue “existe un modelo regional adecuado de precipitaciones máximas en la región Moquegua”. Las hipótesis especificas fueron: la relación existente entre las precipitaciones máximas con los factores geográficos es no lineal, y la función de distribución probabilística regional adecuada para las precipitaciones máximas en la región es la distribución Log-Pearson tipo III. El objetivo general fue realizar la regionalización de precipitación máxima de 24 horas en la región Moquegua. Los objetivos específicos fueron: determinar la relación que existe entre las precipitaciones máximas con los factores geográficos, y determinar la función de distribución probabilística regional adecuada para las precipitaciones máximas en la región.
MATERIALES Y MÉTODOS
ÁMBITO O LUGAR DE ESTUDIO
La región Moquegua se sitúa entre 15°17’ y 17°23’ de latitud sur, se localiza en la parte sur del territorio peruano, limitado por el norte con la región Arequipa, por el este con la región Puno, por el sur con la región de Tacna y por el oeste con el océano Pacifico (INEI, 2000). La oferta hídrica en la región Moquegua proviene de dos ríos de la vertiente del Pacífico: el río Tambo y el río Moquegua (INRENA, 2003). Posee 4 regiones geomorfológicas: Costa, Zona Altoandina, Zona Inferior andina y Zona Meso andina. Presenta condiciones térmicas variables, cálidas en los sectores inferiores y frío en las altiplanicies andinas, donde se observan algunos picos con nieves permanentes. En base a los criterios de Köppen, posee 3 tipos de clima: Clima semicálido muy seco (desértico o árido subtropical), clima templado sub - húmedo (Estepa y valles interandinos bajos) y clima frío o boreal (Valles mesoandinos). El Clima Semi - Cálido muy Seco, comprende casi toda la Costa, desde el litoral del Pacífico hasta el nivel aproximado de 2000 m.s.n.m., tiene precipitación promedio anual de 150 mm y temperaturas medias anuales de 18° a 19° C, decreciendo a niveles más elevados. El Clima Templado Sub-Húmedo, o “clima de montaña baja”, es propio de la sierra, correspondiendo principalmente a los valles interandinos bajos e intermedios, situados entre los 1000 y 3000 m.s.n.m., sus temperaturas sobrepasan los 20° C y la precipitación anual se encuentra por debajo de los 200 mm, aunque en las partes más elevadas, húmedas y orientales, puede alcanzar y eventualmente sobrepasar los 300 mm. El Clima Frío o Boreal, se extiende entre los 3000 y 4000 m.s.n.m., se caracteriza por sus precipitaciones anuales promedio de 300 mm y por sus temperaturas anuales de 12° C; comprende los valles mesoandinos propios de los sectores central y meridional de los andes, presenta veranos lluviosos e inviernos secos con heladas. En la región de acuerdo con la clasificación de zonas de vida del Dr. L.R. Holdridge hay 13 unidades ecológicas (INRENA, 2003).
DESCRIPCIÓN DE MÉTODOS
Primer objetivo específico. Realizar la regionalización de precipitación máxima de 24 horas.
Se recopiló información de precipitaciones máximas de 24 horas en la región Moquegua.
Se utilizó información pluviométrica dentro de la región Moquegua, en su mayoría registrada por el Servicio Nacional de Meteorología e Hidrología (SENAMHI). Las estaciones utilizadas y la longitud de registro de precipitación máxima de 24 horas se presentan en la tabla 1.
Tabla 1. Estaciones meteorológicas utilizadas en el estudio.
| Estación | Altitud (msnm) | Longitud Oeste | Latitud Sur | Longitud de registro |
|---|---|---|---|---|
| Ilo | 60 | 71°17’09.1” | 17°37’43.8” | 1965 a 2009 |
| Moquegua | 1420 | 70°55’50.4” | 17°10’31.4” | 1998 a 2013 |
| Yacango | 2191 | 70°51’56.9” | 17°05’36.7” | 1986 a 2005 |
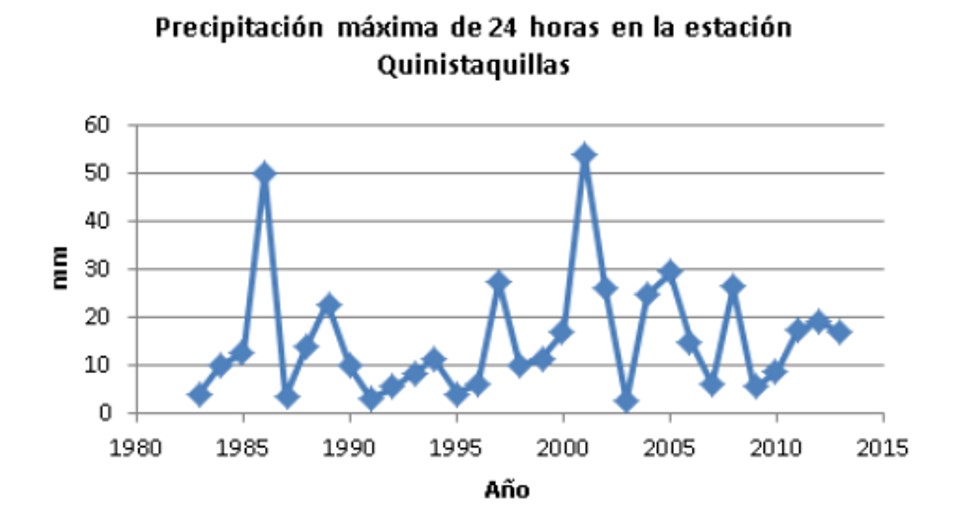
| Quinistaquillas | 1765 | 70°53’49.4” | 16°44’8.6” | 1983 a 2013 |
| Omate | 2130 | 70°58’43.6” | 16°40’29.5” | 1986 a 2013 |
| Puquina | 3109 | 71°10’58.3” | 16°37’34.5” | 1998 a 2013 |
| Carumas | 3150 | 70°41’29.3” | 16°48’44.6” | 1998 a 2013 |
| Ichuña | 3800 | 70°33’7.5” | 16°7’57.4” | 1966 a 2009 |
| Ubinas | 3380 | 70°51’14.2’’ | 16°22’19.4’’ | 1983 a 2013 |
| Calacoa | 3260 | 70°40’58.08’’ | 16°44’6’’ | 1967 a 2009 |
| Cuajone | 3580 | 70°43'0.27" | 17°1'0.74" | 1965 a 1997 |
| Quellaveco | 3550 | 70°37'0.24" | 17°5'59.14" | 1952 a 1998 |
Fuente: SENAMHI.
La información cartográfica utilizada son cartas nacionales en formato digital del Instituto Geográfico Nacional (IGN) a la escala 1:100 000. Se utilizó el sistema de coordenadas UTM WGS84, proyectadas para la zona geográfica respectiva.
Se analizó los estadísticos descriptivos de los registros de precipitación máxima en cada una de las estaciones.
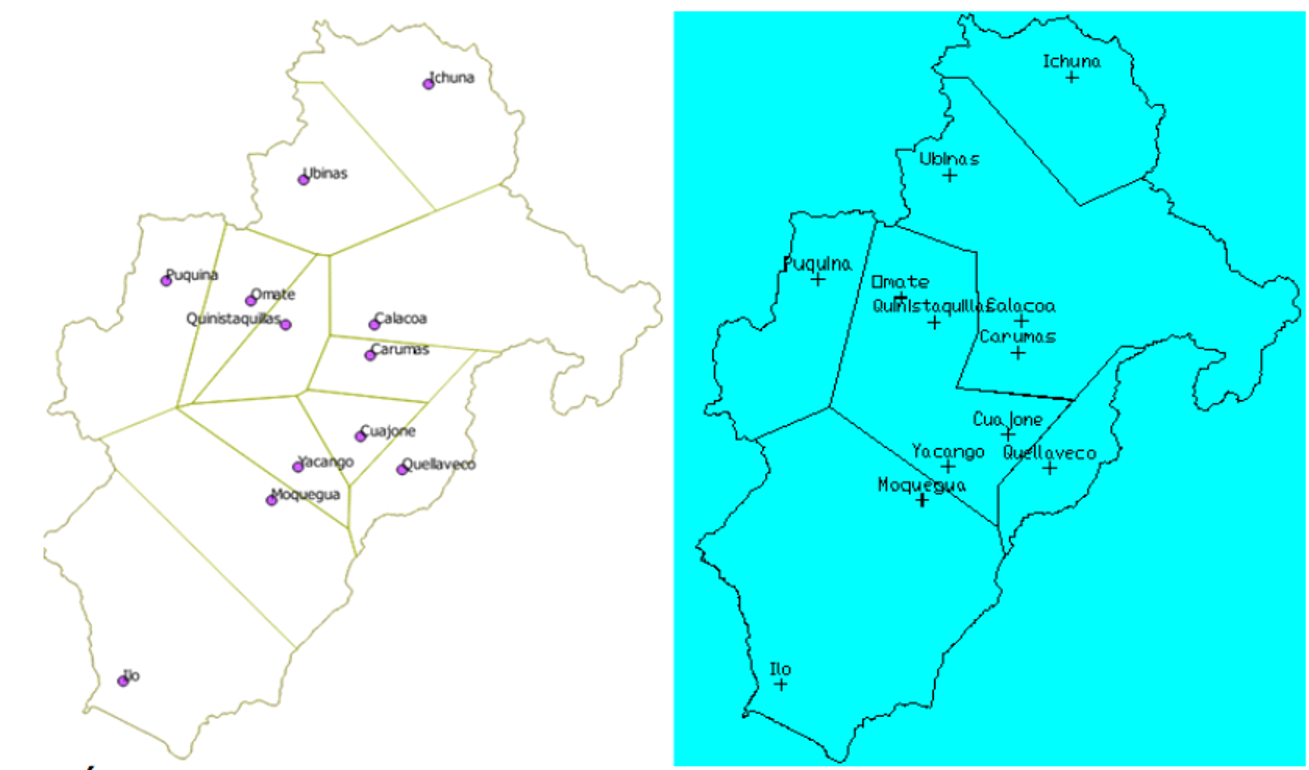
Se utilizó análisis clúster para determinar grupos homogéneas de estaciones con los estadísticos descriptivos de cada estación. Se estableció regiones homogéneas por polígonos de Thiessen o polígonos de Voronoi para cada estación luego estos se agregaron para formar regiones homogéneas.
Para ello se utilizó el software Microsoft Office Word, Microsoft Office Excel, Minitab 15, AutoCAD 2012, Surfer 8.0 y el software para sistema de información geográfica QGIS 2.0.
Segundo objetivo específico. Determinar la función de distribución probabilística regional adecuada para las precipitaciones máximas.
Se realizó la modulación (división entre la media) de las precipitaciones en las estaciones dentro de cada región homogénea. Se determinó mediante modulación la variable reducida siguiente.
Dónde: x’ = variable reducida, x = valor de precipitación máxima de 24 horas, = media de x.
Se seleccionó la distribución de probabilidad más adecuada a través de la prueba de bondad de ajuste de X2 y Kolmogorov-Smirnov en cada región homogénea utilizando el software Hidrognomon.
Tercer objetivo específico. Determinar la relación entre la precipitación máxima y factores geográficos.
Determinación de modelos empíricos que expliquen la media de precipitación máxima en función de coordenadas geográficas y altitud.
Análisis de frecuencia utilizando factores de frecuencia y determinación de las precipitaciones máximas para un período de retorno en cada una de las estaciones.
Determinación de la relación regional entre la precipitación máxima para un período de retorno y la posición geográfica utilizando regresión múltiple.
Dónde: T = Periodo de Retorno, θi = Parámetros del modelo.
RESULTADOS
Primer objetivo específico. Realizar la regionalización de precipitación máxima de 24 horas.
Se graficó las precipitaciones máximas de 24 horas de las estaciones meteorológicas utilizadas. Se presenta a continuación el gráfico de una de las estaciones.
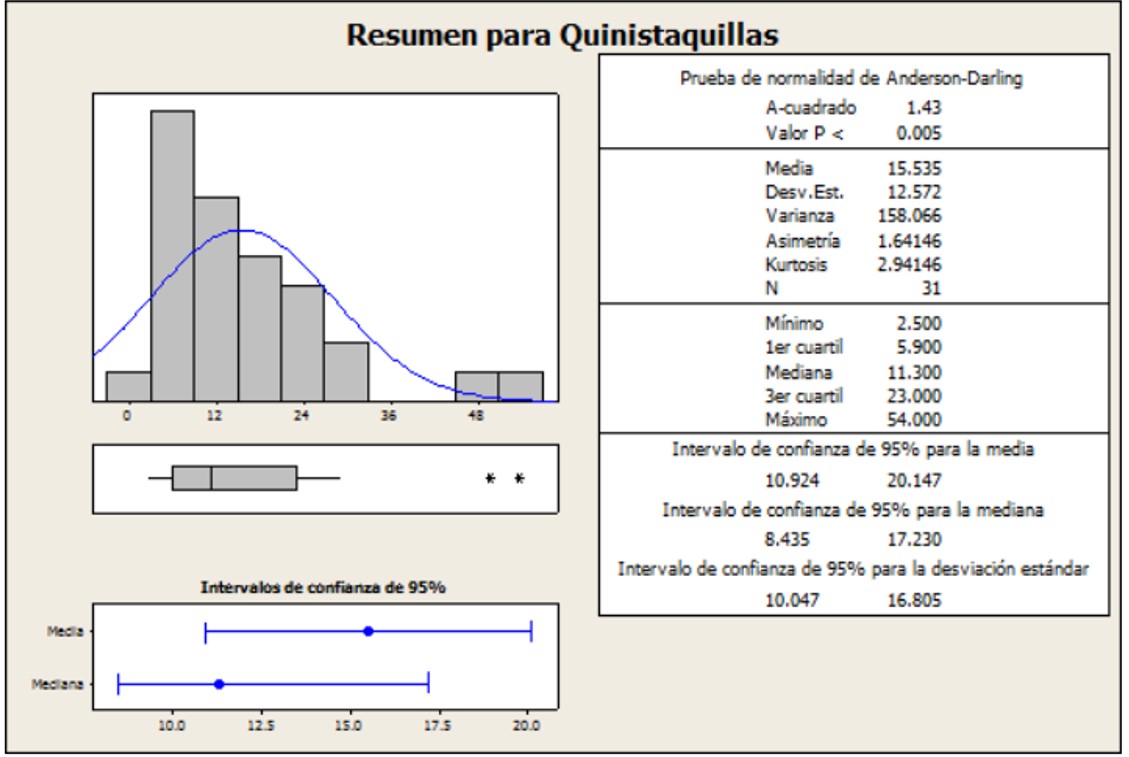
Se realizó un análisis estadístico de los registros de precipitación máxima, para ello se determinó los estadísticos descriptivos de las estaciones meteorológicas utilizadas, a continuación se presenta los estadísticos de una estación meteorológica.
Para la determinación de regiones homogéneas se utilizó el análisis clúster.
En la Tabla 2 se presenta las características de la cada estación para el análisis clúster.
Tabla 2. Características de las estaciones para el análisis clúster
| Estación | Media | Desvest. | Coef.asim. | Coef.curt. | Coef.varia |
|---|---|---|---|---|---|
| Ilo | 1.0561 | 1.3221 | 1.4485 | 1.3923 | 1.2519 |
| Moquegua | 4.7563 | 2.9480 | 0.6159 | 0.3887 | 0.6198 |
| Yacango | 11.6000 | 6.8908 | 0.4187 | -1.0530 | 0.5940 |
| Quinistaquillas | 15.5355 | 12.5724 | 1.6415 | 2.9415 | 0.8093 |
| Omate | 18.5643 | 9.9433 | 0.4081 | -0.1923 | 0.5356 |
| Puquina | 24.0688 | 8.3775 | -0.0180 | -0.5479 | 0.3481 |
| Carumas | 30.9625 | 10.1399 | 1.4622 | 3.0702 | 0.3275 |
| Ichuña | 33.7045 | 14.4121 | 3.7034 | 18.6479 | 0.4276 |
| Ubinas | 23.9742 | 7.9072 | -0.7210 | 1.4301 | 0.3298 |
| Calacoa | 27.3132 | 11.3866 | 1.0568 | 1.0242 | 0.4169 |
| Cuajone | 14.6009 | 8.9396 | 0.1061 | -1.1876 | 0.6123 |
| Quellaveco | 20.1718 | 13.1659 | 2.5967 | 8.9662 | 0.6527 |
Fuente: Elaboración propia
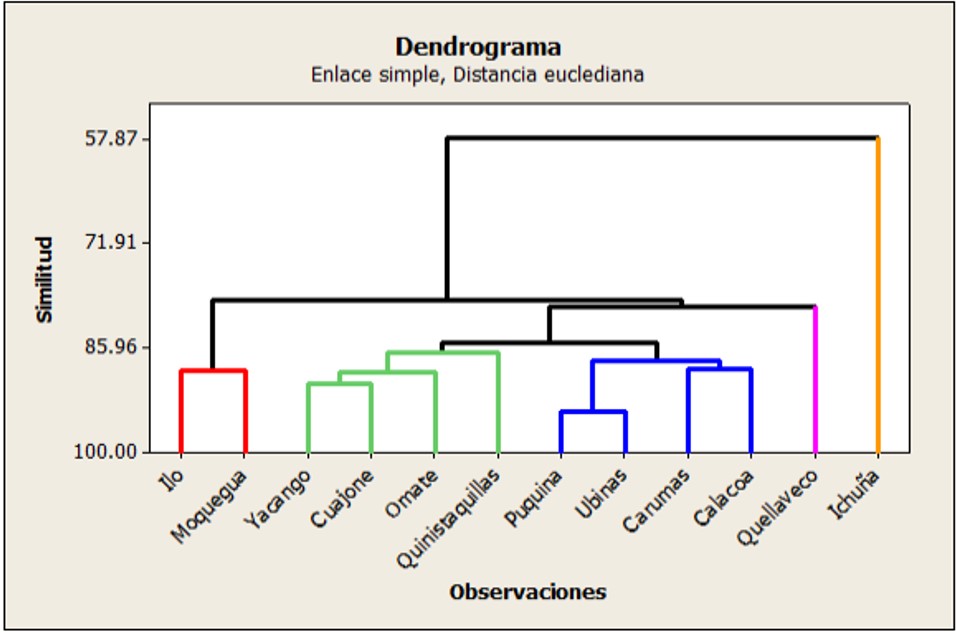
Según el dendograma las regiones son las siguientes mostradas en la tabla 3.
Tabla 3. Regiones homogéneas en estadísticos muestrales de precipitación máxima.
| Región homogénea | Estaciones meteorológicas |
|---|---|
| 1 | Ilo, Moquegua |
| 2 | Yacango, Cuajone, Omate, Quinistaquillas |
| 3 | Puquina, Ubinas, Carumas, Calacoa |
| 4 | Quellaveco |
| 6 | Ichuña |
El área de influencia de cada estación se determinó mediante el trazado de polígonos de Voronoi. Según las regiones determinadas por análisis clúster se agregó estas áreas de influencia, obteniéndose la figura siguiente.
Segundo objetivo específico. Determinar la función de distribución probabilística regional adecuada para las precipitaciones máximas.
Los resultados de la prueba de bondad de ajuste X2 (para 8 intervalos) y de Kolmogorov-Smirnov al 0.05 de significancia para la variable reducida de cada región homogénea, de las 05 regiones, muestran las siguientes distribuciones de mejor ajuste para cada región homogénea.
Tabla 4. Distribuciones de probabilidad de mejor ajuste en las regiones homogéneas.
| Región | Distribución de probabilidad |
|---|---|
| 1 | Pareto |
| 2 | Pareto (L-Moments) |
| 3 | GEV-Min (L-Moments) |
| 4 | EV2-Max |
| 5 | EV2 Max (L-Momments) |
Tercer objetivo específico. Determinar la relación entre la precipitación máxima y factores geográficos.
La relación entre la media de la precipitación máxima y la posición geográfica en las regiones homogéneas ha sido determinada. En la región 1 debido a que se tiene dos estaciones simplemente es una recta de ajuste lineal siguiente.
Dónde: Altitud = altitud de la estación (m.s.n.m.), media = media de la precipitación máxima (mm).
En la región 2 se determinó una relación entre la media de precipitación máxima y la posición geográfica, siendo la variable Latitud la mejor variable independiente. La cual se determinó por regresión y se presenta en la Tabla 5.
Tabla 5. Análisis de regresión entre la media de precipitación máxima y la posición geográfica en la región 2
| Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
| Constante | 225.92 | 73.61 | 3.07 | 0.092 |
| Latitud Sur | -12.491 | 4.361 | -2.86 | 0.103 |
Tabla 6. Análisis de varianza de regresión para la región 2
| Fuente | GL | SC | MC | F | P |
|---|---|---|---|---|---|
| Regresión | 1 | 19.849 | 19.849 | 8.20 | 0.103 |
| Error residual | 2 | 4.838 | 2.419 | ||
| Total | 3 | 24.688 |
En la región 3 se determinó una relación entre la media de precipitación máxima y la posición geográfica. La cual se determinó por regresión y se presenta en la Tabla 7.
Tabla 7. Análisis de regresión entre la media de precipitación máxima y la posición geográfica en la región 3
| Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
| Constante | 328.8 | 437.6 | 0.75 | 0.590 |
| Longitud Oeste | -6.860 | 5.440 | -1.26 | 0.427 |
| Latitud Sur | 11.051 | 6.620 | 1.67 | 0.344 |
Tabla 8. Análisis de varianza de regresión para la región 3
| Fuente | GL | SC | MC | F | P |
|---|---|---|---|---|---|
| Regresión | 2 | 28.628 | 14.314 | 3.40 | 0.358 |
| Error residual | 1 | 4.213 | 4.213 | ||
| Total | 3 | 32.840 |
Tabla 9. Medidas de bondad de ajuste de regresión
| Región | S | R2 (%) | R2ajustado(%) | Modelo |
|---|---|---|---|---|
| 2 | 1.55539 | 80.4 | 70.6 | Media = 226 - 12.5 (Latitud Sur) |
| 3 | 2.05247 | 87.2 | 61.5 | Media = 329 - 6.86 (Longitud Oeste) + 11.1 (Latitud Sur) |
En las regiones 4 y 5 no se determinaron las relaciones porque estas regiones solo poseen una estación cada una, por lo cual no es factible plantear estas relaciones. Se presenta los resultados del análisis de frecuencia utilizando factores de frecuencia. En la región 1 se tiene los siguientes valores de variable reducida para los periodos de retorno, además de los valores de precipitación máxima determinados para cada estación de esta región, como muestra la Tabla 10.
Tabla 10. Variable reducida y precipitación máxima por estación en la región 1 y 2.
| Región 1 | Región 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| T | x’ | Ilo | Moquegua | T | x’ | Yacango | Cuajone | Omate | Quinistaquillas |
| 25 | 2.68248 | 2.83 | 12.76 | 25 | 2.27445 | 26.38 | 33.21 | 42.22 | 35.33 |
| 50 | 3.01997 | 3.19 | 14.36 | 50 | 2.44642 | 28.38 | 35.72 | 45.42 | 38.01 |
| 100 | 3.30317 | 3.49 | 15.71 | 100 | 2.57152 | 29.83 | 37.55 | 47.74 | 39.95 |
| 200 | 3.54081 | 3.74 | 16.84 | 200 | 2.66251 | 30.89 | 38.88 | 49.43 | 41.36 |
T = período de retorno (años), X’ = variable reducida
Tabla 11. Variable reducida y precipitación máxima por estación en la región 3, 4 y 5.
| Región 3 | Región 4 | Región 5 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T | x’ | Puquina | Ubinass | Carumas | Calacoa | T | x’ | Quellaveco | T | X’ | Ichuña |
| 25 | 1.6852 | 40.56 | 40.40 | 52.18 | 46.03 | 25 | 2.1169 | 42.70 | 25 | 1.7742 | 59.80 |
| 50 | 1.8283 | 44.00 | 43.83 | 56.61 | 49.94 | 50 | 2.6632 | 53.72 | 50 | 2.0993 | 70.75 |
| 100 | 1.9599 | 47.17 | 46.99 | 60.68 | 53.53 | 100 | 3.3449 | 67.47 | 100 | 2.4808 | 83.61 |
| 200 | 2.0826 | 50.12 | 49.93 | 64.48 | 56.88 | 200 | 4.1976 | 84.67 | 200 | 2.9299 | 98.75 |
T = período de retorno (años), X’ = variable reducida
La relación entre las precipitaciones máximas y la posición geográfica para la región Moquegua, en base a regresión múltiple es.
En la Tabla 12 se presenta los resultados del análisis de regresión. El modelo posee un S = 10.0099, R2 = 78.9% y R2 ajustado = 77.0%
Tabla 12. Resultados del análisis de regresión
| Predictor | Coef | SE Coef | T | P |
|---|---|---|---|---|
| Constante | 2336.0 | 757.4 | 3.08 | 0.004 |
| T | 0.06751 | 0.02156 | 3.13 | 0.003 |
| ALTITUD | 0.006288 | 0.002518 | 2.50 | 0.016 |
| LONGW | -27.73 | 10.37 | -2.67 | 0.011 |
| LATSUR | -20.874 | 5.293 | -3.94 | 0.000 |
Tabla 13. Análisis de varianza de regresión
| Fuente | GL | SC | MC | F | P |
|---|---|---|---|---|---|
| Regresión | 4 | 16125.5 | 4031.4 | 40.23 | 0.000 |
| Error residual | 43 | 4308.5 | 100.2 | ||
| Total | 47 | 20434.0 |
La Tabla 12 que los coeficientes de regresión son estadísticamente significativos al 95% de confianza. El coeficiente de determinación muestra que el 78.9% de la varianza de la precipitación máxima es explicado por el modelo lineal. El análisis de varianza muestra que el coeficiente de determinación es significativo al 95% de confianza. Existe una distribución de probabilidad por cada región homogénea, por lo cual, no se realizó la determinación de la relación regional entre los parámetros de la función de distribución de probabilidad y la posición geográfica, porque hay solo un grupo de parámetros por cada región homogénea y hay varias estaciones en cada región, por consiguiente, no existe los pares ordenados para realizar la regresión.
La variación espacial de la precipitación en estas investigaciones se trató de manera agregada, y no tiene correspondencia con las variables geográficas de posición, sin embargo, sus objetivos no han sido centrados en este aspecto. La regionalización que se plantea en esta investigación puede aplicarse para distribuir mejor la precipitación de diseño para luego realizar la transformación precipitación-escorrentía.
DISCUSIÓN
En cada región homogénea se ha escogido una distribución de probabilidad con las pruebas de bondad de ajuste tal como recomienda Aparicio (Aparicio, 2010). En este estudio se ha utilizado precipitaciones diarias anuales tal como lo recomienda Bolainas-Castillo y otros (Bolainas Castillo et al., 2011). A diferencia de la investigación de Benhamrouche y Martín (Benhamrouche & Martín Vide, 2011) la presente investigación no ha tomado en cuenta la concentración de la lluvia, sino solamente la profundidad de lluvia diaria máxima en un año. El método de regionalización utilizado en nuestra investigación determina regiones homogéneas por análisis clúster, es un método alternativo al método de L-momentos en el que hicieron análisis de conglomerados (Malekinezhad & Zare-Garizi, 2014), además otras investigaciones obtuvieron una distribución diferente para cada región homogénea, estos autores atribuyen este hecho a las condiciones climáticas y geográficas diferentes entre regiones homogéneas, lo cual también se presenta en nuestra investigación.
Otros autores también aplicaron el método de L-momentos, la prueba de Fisher y de discordancia (Aguilar Suarez et al., 2017) para determinar regiones homogéneas del mismo modo hicieron otros investigadores (Malekinezhad & Zare-Garizi, 2014), además otros investigadores (Aguilar Suarez et al., 2017), obtuvieron un nuevo grupo o una región homogénea de 59 estaciones en la cual la distribución de mejor ajuste fue la TCEV, ellos realizaron la modulación (dividir los datos entre la media) de datos así como nosotros lo hicimos en cada región homogénea. También otros autores al igual que nuestro estudio se obtuvieron precipitaciones de diseño para diferentes períodos de retorno (Aguilar Suarez et al., 2017). La presente investigación ha seleccionado la distribución de probabilidad con la prueba de bondad de ajuste Chi cuadrado al igual que otros autores (Baghel et al., 2019). La presente investigación no ha considerado la concentración de precipitación en espacio y tiempo, tampoco datos mensuales como lo hizo la investigación de Ilbay-Yupa y otros (Ilbay-Yupa et al., 2019) porque se ha trabajado con precipitación máxima diaria. En la presente investigación se ha utilizado información puntual de estaciones a diferencia de otras investigaciones que utilizan imágenes TRMM (Chikalamo et al., 2020) las cuales muestran una variación continua pero que tiene limitaciones en la resolución espacial. El estudio realizado es en el sur del Perú donde están presentes los factores que afectan las lluvias extremas del Pacífico Sur (Pariyar et al., 2020) los cuales entre otros son: ciclones tropicales, la oscilación de Madden-Julian y El niño-Oscilación del sur.
Se concluye que, la regionalización de precipitación máxima de 24 horas en la región Moquegua, se realizó con análisis clúster obteniéndose cinco regiones homogéneas, las distribuciones de probabilidad más adecuadas para las respectivas regiones son: para región 1 la distribución de Pareto, para la región 2 la distribución de Pareto estimado por L-momentos, para región 3 la distribución de valor extremo generalizada para mínimos estimada por L momentos, para la región 4 la distribución de valor extremo tipo 2 y para la región 5 la distribución de valor extremo tipo 2 estimada por L-momentos.
Al determinar la relación que existe entre las precipitaciones máximas con los factores geográficos en la región Moquegua, después de un análisis de frecuencia en cada región homogénea se determinó una relación lineal entre precipitación máxima, periodo de retorno, coordenadas geográficas y altitud, que tiene un coeficiente de determinación de 0.789 con todos los coeficientes estadísticamente significativos al 0.05 de nivel de significancia.
Al determinar la función de distribución probabilística regional adecuada para las precipitaciones máximas en la región Moquegua, estas son las cinco distribuciones de probabilidad para las respectivas regiones homogéneas. En esta investigación se aplicó una metodología alternativa a las metodologías de regionalización de precipitación máxima de 24 horas.
RECONOCIMIENTOS
Se agradece a las instituciones que han permitido el acceso a la información de precipitación máxima de 24 horas y a la información cartográfica.