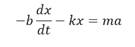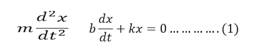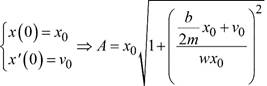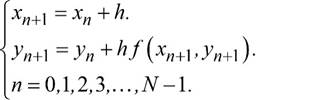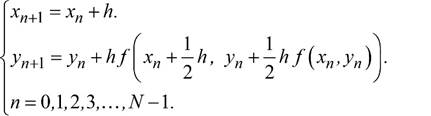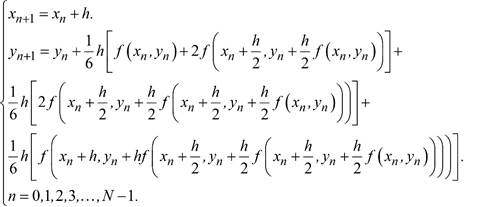Introducción
La apariencia del movimiento armónico amortiguado generalmente está relacionada con un cuerpo de cierta masa unido a un extremo de una fuente elástica, permaneciendo fijo el otro extremo de dicha fuente. De hecho, es un tema estudiado en modelos matemáticos y físicos.
En términos matemáticos según Costa et al., (2011), el estudio del movimiento armónico amortiguado se desarrolla por medio de las ecuaciones diferenciales que, en la mayoría de los casos, por medio de métodos usuales de resolución, se obtiene una solución analítica para pequeñas intensidades de amortiguamiento.
Los trabajos realizados hasta el momento presentan diferentes enfoques y aplicaciones, por ejemplo, en (Pascual et al.,2008) se realiza una simulación en Maple de la modelación del movimiento tanto armónico simple como amortiguado, en (Serrano et al.,2016) se presenta un caso del modelado y solución de una ecuación diferencial ordinaria de segundo orden considerando un sistema masa resorte con movimiento libre amortiguado, resuelta analíticamente y simulada con el apoyo del software GeoGebra, en González (2009) se estudian las ecuaciones diferenciales ordinarias lineales de segundo orden de coeficientes constantes que describe este problema con algunas aplicaciones físicas, en Rodríguez (2019). se construye un modelo matemático para explicar o describir la acción de los terremotos sobre edificios de varios pisos, mediante ecuaciones diferenciales de segundo orden de sistema masa resorte.
La motivación de este trabajo es encontrar soluciones numéricas adecuadas para la ecuación diferencial que describe el movimiento armónico amortiguado, implementando algunas funciones ODE de Matlab, así como métodos numéricos de diferentes órdenes, que permiten resolver ecuaciones diferenciales ordinarias con condiciones iniciales establecidas.
El objetivo de este artículo es resolver numéricamente la ecuación diferencial del movimiento armónico amortiguado. Se implementarán las funciones ODE23, ODE45 y ODE113 de Matlab y algunos métodos numéricos de orden 1, de orden 2, orden 3 y orden 4 con condiciones iniciales a la ecuación diferencial del problema estudiado y posteriormente, se compararán con la solución analítica obtenida para pequeñas intensidades de amortiguamiento.
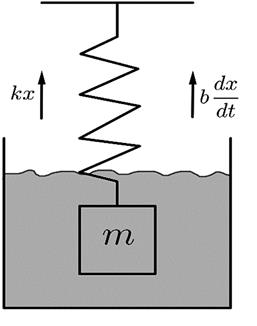
Según (Sears et al., 2013) y Molina (2016), un sistema amortiguado es un esquema sencillo que se puede observar en la Figura 1.
Se puede observar un cuerpo de masa m suspendido de un resorte de constante k, que oscila, tiene movimiento armónico amortiguado, cuando la fricción del medio sobre la masa fr es directamente proporcional a la velocidad, esto es
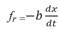 , siendo b la constante de amortiguamiento y
, siendo b la constante de amortiguamiento y
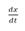 es la velocidad de masa.
es la velocidad de masa.
Como la masa está sujeta a un resorte, entonces estará sometida a una fuerza de origen elástica dada por la ecuación F = - k x, siendo k la constante elástica del resorte que depende de la geometría y del material del cual está hecho y x es la elongación del resorte a partir de su posición de equilibrio.
El efecto del peso no se considera porque se compensa con la deformación inicial que sufre el resorte al colgarle la masa m y de esta manera, se dice que el sistema está en la posición de equilibrio, se toma como positivo el desplazamiento hacia abajo, por eso los signos de la fuerza elástica y la retardadora se consideran negativos, pues actúan hacia arriba.
Para obtener la ecuación de movimiento se aplica la segunda ley de Newton al sistema masa resorte y se obtiene el siguiente resultado:
donde a
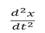 es la aceleración de la masa, de esta forma, el movimiento armónico amortiguado de la Figura 1, quedará descrito por la ecuación diferencial:
es la aceleración de la masa, de esta forma, el movimiento armónico amortiguado de la Figura 1, quedará descrito por la ecuación diferencial:
De esta manera, mediante la aplicación de los métodos usuales de resolución, la solución analítica de la ecuación (1) para pequeñas intensidades de amortiguamiento
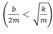 , está dada por: x (t)=
, está dada por: x (t)=
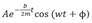 ; con w=
; con w=
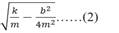
En la ecuación (2), las constantes de integración, A, y ϕ (amplitud y desfase) se calculan de mediante las condiciones iniciales:
Métodos
Métodos numéricos para ecuaciones diferenciales
En la mayoría de los casos, es muy difícil encontrar soluciones exactas de una ecuación diferencial por medio de métodos usuales, en este contexto, la apli cación de métodos numéricos es indispensable para obtener soluciones aproximadas. Generalmente según (Prima et al.,2000), León (2015) y (Atkinson et al., 2011), los métodos numéricos son utilizados añadiendo condiciones iniciales a la ecuación diferencial a estudiar.
Considere el problema de valor inicial de primer orden: y´= f(x,y); y(x 0 )=y 0 ……..(3)
Sea
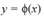 una solución exacta única de la ecuación (3) en algún intervalo centrado en x = x
0, con el supuesto de que f y fy son continuas en algún rectángulo del plano xy que contenga al punto (x0, y0).
una solución exacta única de la ecuación (3) en algún intervalo centrado en x = x
0, con el supuesto de que f y fy son continuas en algún rectángulo del plano xy que contenga al punto (x0, y0).
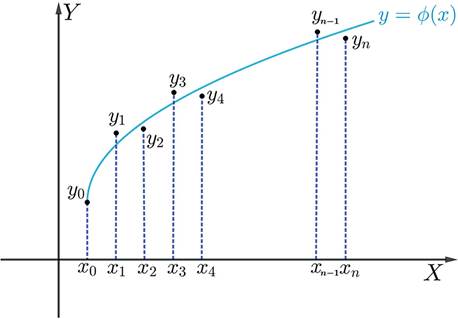
Para encontrar soluciones aproximadas, en mé todos numéricos se emplean algoritmos iterativos de resolución que calculan los valores aproximados y0, y1, y2, …, yn, … de la solución
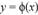 de la ecuación (3) en un conjunto de puntos x0, x1, x2, …, xn, …, como se muestra en la Figura 2.
de la ecuación (3) en un conjunto de puntos x0, x1, x2, …, xn, …, como se muestra en la Figura 2.
En la Figura 2 se tiene que y (x
0) = y por el problema de valor inicial, pero
 1, además,
1, además,

También sobre el eje x se realizará un espaciamiento o tamaño de paso uniforme h, así entonces x 1 =x 0 +h; x 2 =x 0 +2h;…;x n =x 0 +nh
Los métodos numéricos se dividen en dos grupos, métodos de un paso donde se utiliza la solución aproximada yn en xn para obtener la solución aproximada yn+1 en xn+1 y en los métodos multipaso la solución yn+1 se obtiene utilizando el valor o los valores de solución calculados en los puntos anteriores.
El orden de un método numérico es un entero no negativo p de modo que
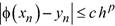 para alguna constante c.
para alguna constante c.
En este artículo, se utilizarán métodos numéricos de un paso y multipaso conjuntamente, además se implementarán y se compararán según el orden de
Métodos numéricos implementados en la resolución
Los siguientes métodos numéricos implementados en este artículo, resuelven numéricamente el proble ma de valor inicial (3), en un intervalo cerrado a,b, donde x0 = a, xn+1 = b y en N pasos. Primeramente se divide el intervalo a,b en N partes iguales de longitud
 posteriormente se aplica el algoritmo correspondiente a cada método.
posteriormente se aplica el algoritmo correspondiente a cada método.
Método de Euler backward de orden 1.
Datos: x 0 , y 0 ,h, f (x,y),N
Algoritmo:
Método de Runge Kutta de orden 2.
Datos: x 0 , y 0 ,h, f (x,y),N
Algoritmo:
Método de Adams Moulton de orden 3.
Datos: x0 , x1 , y0 , y1 ,h, f(x,y),N.
Algoritmo:
Método de Runge Kutta de orden 4.
Datos: x 0 , y 0 ,h, f(x,y),N.
Algoritmo:
Las funciones ODE de Matlab.
Las funciones ODE de Matlab proporcionan una solución numérica de ecuaciones diferenciales ordinarias con problemas de valores iniciales, cuando es difícil encontrar la solución analítica de la mencionada ecuación diferencial. Se implementaron debido a la ineficiencia del método de Euler en las aplicaciones. 9
En este trabajo se implementarán las funciones ODE23, ODE45 y ODE113 para resolver la ecuación (1) con algunas condiciones iniciales establecidas.
El uso de las funciones ODE en código de Matlab se describe a continuación.
T,Y=ODE(odefun,tspan,Y 0 )
odefun es un identificador de función, que puede ser un nombre de archivo de función, un identificador de función anónimo o un nombre de función en línea.
tspan es el intervalo x0 , xn +1 o una serie de puntos dispersos x 0 , x 1 , …,x n+1 .
Y 0 es el vector de valor inicial.
T devuelve el tiempo del vector de columna.
Y devuelve el vector de la columna de so lución correspondiente a T.
Resultados y discusión
Para la implementación de los algoritmos mencionados anteriormente, se consideraron la ecuación diferencial
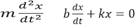 que describe el movimiento armónico amortiguado, donde
que describe el movimiento armónico amortiguado, donde
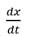 representa la velocidad del movimiento vertical de la masa, con las siguientes condiciones iniciales, x(0)=1 y x´(0)=0.
representa la velocidad del movimiento vertical de la masa, con las siguientes condiciones iniciales, x(0)=1 y x´(0)=0.
Se presentarán a continuación, los resultados obtenidos para la solución analítica x(t) y para la velocidad del movimiento vertical de la masa
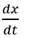
Resultados de la implementación de las funciones ODE de Matlab.
En la Figura 3 se muestra la comparación de las funciones ODE23, ODE45 y ODE113 con la solución exacta x(t), mediante una experimentación numérica en el intervalo 0,30.
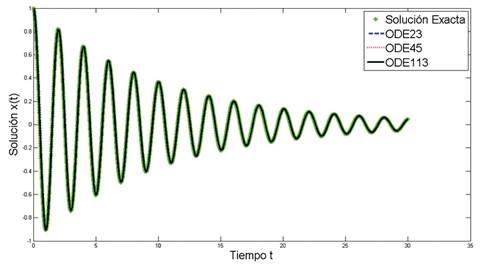
Figura 3. Soluciones numéricas para x(t) en el intervalo 0,30, con h = 0.0075, N = 400, m = 1, b = 0.2 y k = 9.81.
En la Figura 4 se muestra la comparación de las funciones ODE23, ODE45 y ODE113 con la velocidad del movimiento vertical de la masa
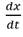 mediante una experimentación numérica en el intervalo 0,30.
mediante una experimentación numérica en el intervalo 0,30.
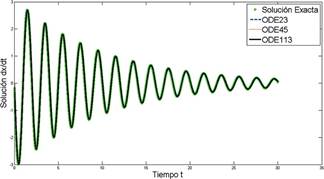
Figura 4. Soluciones numéricas para dx/dtd en el intervalo(0,30), con h = 0.0075, N = 400, m = 1, b = 0.2 y k = 9.81.
Resultados de la implementación de los métodos numéricos de orden 1, de orden 2, de orden 3 y de orden 4 descritos en este trabajo.
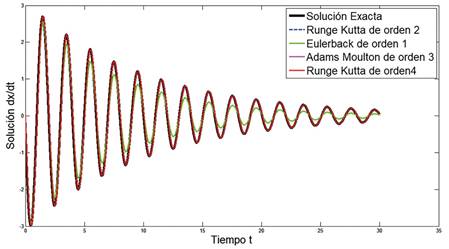
En la Figura 5 se muestra la comparación de las soluciones numéricas de los métodos Euler backward de orden 1, Runge Kutta de orden 2, Adams Moulton de orden 3 y Runge Kutta de orden 4 con la solución exacta x(t), mediante una la experimentación numérica en el intervalo 0,30.
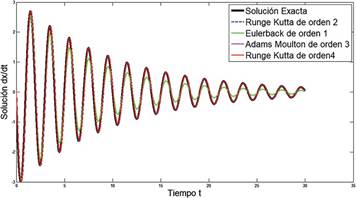
Figura 5. Soluciones numéricas para x(t) en el intervalo (0,30), con h = 0.0075, N = 400, m = 1, b = 0.2 y k = 9.81.
En la Figura 6 se muestra la comparación de las soluciones numéricas de los métodos Euler backward de orden 1, Runge Kutta de orden 2, Adams Moulton de orden 3 y Runge Kutta de orden 4 con la velocidad del movimiento vertical de la masa
 mediante una la experimentación numérica en el intervalo 0,30.
mediante una la experimentación numérica en el intervalo 0,30.
Conclusiones
En este trabajo se han realizado soluciones numéricas para pequeñas intensidades de amortiguamiento del problema que describe el movimiento armónico amortiguado representado mediante ecuaciones diferenciales, la cual presenta solución analítica real para la condición dada, posteriormente, se han implementados algunos métodos numéricos, así como las funciones ODE23, ODE45 y ODE113 de Matlab, para realizar una comparación con la problema solución analítica exacta del modelo estudiado y con la velocidad del movimiento vertical de la masa.
A continuación, se presentan las conclusiones sobre la comparación de las distintas funciones ODE de Matlab con las soluciones exacta y de velocidad vertical.
Las funciones ODE23, ODE45 y ODE113 incorporadas en Matlab permiten resolver de manera eficiente ecuaciones diferenciales ordinarias con problema de valor inicial, sobre la implementación de estas funciones al modelo estudiado se puede concluir que, la función ODE113 presenta más aproximación a las soluciones analíticas exacta y de velocidad vertical, debido a su número de orden.
En general, no hay mucha diferencia entre las funciones ODE de Matlab y se pueden ser consideradas como las soluciones numéricas más exactas para ecuaciones diferenciales ordinarias con problema de valor inicial.
Con relación a los métodos numéricos aplicados, el método de orden 1 Eulerback, es el que presenta menor aproximación a las soluciones analíticas exactas y de velocidad vertical, el resultado del método numérico de orden 2, Runge Kutta, presenta una notable mejoría respecto al resultado del método de orden 1. Sin embargo, los métodos de orden 3 y de orden 4 son los que se aproximan de manera eficiente a las soluciones analíticas exactas y de velocidad vertical, siendo el método Runge Kutta de orden 4 la mejor.
Para la resolución numérica de este tipo de problemas de valor inicial se recomienda la implementación de cualesquiera de las funciones ODE de Matlab y de los métodos numéricos, el método de Runge Kutta de orden 4 es el indicado.











 uBio
uBio