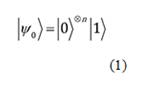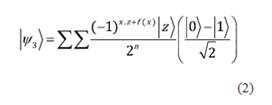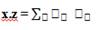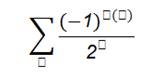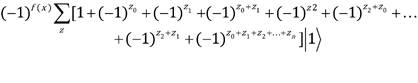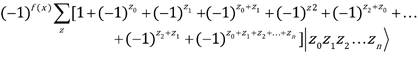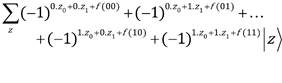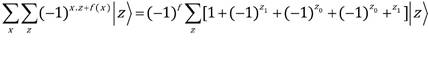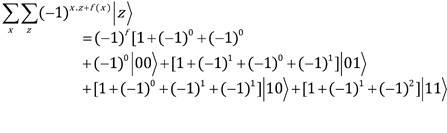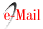Introducción
Existen diversos algoritmos cuánticos en áreas como la criptografía, búsqueda y optimización, simulación de sistemas cuánticos y resolución de sistemas de ecuación lineal (Montanaro, 2016).
El circuito que implementa el algoritmo Deutsch-Jozsa se esquematiza en la Figura 1. Se define el estado inicial como sigue: simulación de sistemas cuánticos y resolución de sistemas de ecuaciones lineales (Montanaro, 2016). Entre esos problemas existe uno que consiste en lo siguiente: dada una función binaria, y asumiendo que la misma puede ser ´únicamente constante o balanceada, distinguir cada caso. Un computador clásico debe evaluar la función 2 n−1 + 1 veces, para una función con n bits de entrada, con el fin de llevar a cabo esta tarea.
El algoritmo Deusch-Jozsa es el algoritmo cuántico que resuelve el problema planteado. Este algoritmo se ha simulado (Chuang, Vandersypen, Zhou, Leung, & Lloyd, 1998), y se han obtenido resultados en un solo paso, en lugar de una cantidad exponencial de pasos. Dicho algoritmo no posee muchas aplicaciones, aunque ha sido utilizado en el contexto de lenguajes formales (Batty, Casaccino, Duncan, Rees, & Severini, 2008).
Se presenta el algoritmo de Deutsch-Jozsa para tener una visión del poder de cómputo que tiene la computación cuántica, este poder de cómputo se basa en el paralelismo, el cual se caracteriza por el crecimiento exponencial, en relación al número de cubits, de la capacidad de realizar operaciones de manera simultánea.
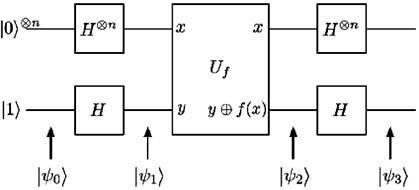
El circuito que implementa el algoritmo Deustch-Jozsa se esquematiza en la Figura 1. Se define el estado inicial como sigue:
Al introducir el estado (1) en el circuito de la Figura 1 el mismo realiza las operaciones indicadas y se obtiene el estado final (Nielsen & Chuang, 2002):
Después de pasar por el circuito de la Figura 1, los primeros n cubits son medidos. Al estado resultante luego de la medición lo denominaremos |ψ 4. La forma que presenta la ecuación (2) nos permite diferenciar fácilmente entre una función balanceada y una constante.
Para implementar los algoritmos cuánticos, IBM permite el acceso a su computador cuántico, o simuladores del mismo, de manera online. Qiskit (Qiskit Development Team, 2020) es un framework de código abierto para diseñar circuitos cuánticos y ejecutarlos en simuladores y computadores cuánticos reales creada por IBM y está basado en Python. Constituye una herramienta muy potente y accesible para ejecutar algoritmos cuánticos.
Se realiza un análisis de la ecuación (2) atendiendo principalmente a la manera en la cual la misma es capaz de realizar la tarea planteada. Con esto en mente, se plantea un ejemplo con dos cubits, se espera que el mismo facilite la comprensión del procedimiento que sigue el algoritmo Deutsch- Jozsa. Para finalizar se ejecuta el algoritmo para 3 cubits en la plataforma IBM Quantum Experience con la ayuda de Qiskit.
Notación
Las variables x y z, en la ecuación (2), representan las distintas combinaciones de ceros y unos posibles. Por ejemplo: dado el estado |0010〉 de 4 cubits, tenemos los siguientes valores:
Z0 = 0, Z1 = 1
Z2 = 0, Z3 = 3
Entonces, una ᴢ posible puede ser:
Z = (z3, z2, z1, z0) = (0,0,1,0)
Y el estado al que hacemos referencia será |Z〉 = |z3 z2 z1 z0〉 =|0010〉 para ese valor especifico de z. La misma notación se utiliza para la variable x.
Cabe destacar que al escribir x z se entenderá lo siguiente
Análisis
Al analizar los posibles resultados post-medicación, contemplamos los siguientes casos:
a) Todos los bits medidos son cero:
En este caso, se tiene que la amplitud de |0〉⊗𝑛 es:
En caso de que la función sea constante, esta amplitud será 1 o −1 dependiendo del valor cons tante que tome f(x). Es fácil notar que cuando todos los bits medidos son cero, la función no puede ser balanceada, ya que eso haría que la amplitud fuera cero, lo cual es impensado para un estado válido (su norma debe ser unitaria).
b) Al menos un bit es distinto de cero:
En el caso en el que al menos un bit resulte ser 1, cabe el análisis de las dos ´únicas situaciones posibles: que la función sea balanceada o que la función sea constante. En caso de que la función sea balanceada no hay mucho que decir, ya que con el análisis anterior queda claro que la ´única manera de que la función sea balanceada es medir al menos un bit distinto de cero, pudiendo ser cualquier combinación con cualquier cantidad de unos el resultado de la medición. En cambio, al pensar en la posibilidad de que la función sea constante, actualmente no tenemos suficientes argumentos para asegurar que esta no es una posibilidad válida. Para demostrar que la función no puede ser constante en el caso de medir al menos un uno, analizamos más a fondo la ecuación (2).
Tomaremos el numerador de los n primeros cubits de la ecuación (2). La sumatoria sobre x, en el caso de que la función sea constante, se desarrolla como sigue:
Cada combinación de z da 2n términos en cada término de arriba. Así tenemos en total 2n términos después de desarrollar ambas sumatorias.
Posterior a la medición, la cantidad de términos que se mantienen disminuye nuevamente a 2n, y se obtiene la siguiente suma:
En la suma de arriba, se observa que la suma de los zi depende de las anteriores en todo momento. Por lo tanto, si tomamos z0 = 0 y z1 = 0 esto implicará que todos los demás valores de zi son cero, este caso ya se ha analizado, y la única manera de avanzar en el análisis es decir que z = 1 esto dará que (−1)z0 = -1 y la suma de arriba jamas alcanza el valor 2”, y por lo tanto, ᴪ 4〉 no será un estado valido después de la medición, asi que la única conclusión posible, al medir una cantidad distinta de cero de unos, será que la función es balanceada.
Ejemplo con 2 cubits
Suponiendo que introducimos dos cubits al circuito, es decir n = 2, podemos reemplazar todos los posi bles valores de x en el numerador de los primeros dos cubits de la expresión (2), y obtendremos:
Si la función es constante podemos definir ƭ ≡ƭ (ⅈⅉ) y escribimos
Reemplazando los distintos valores de z obtenemos:
Se observa que al medir y obtener un estado distinto de |00〉 el coeficiente que acompaña al mismo será, en todos los casos, menor que 4 en valor absoluto, por lo tanto, no representara un estado válido, y por ese motivo jamás se medirá un estado distinto al |00〉 cuando la función sea constante.
En resumen, si después de la medición obtenemos el estado |0〉 n ⊗, entonces podemos asegurar que la función es constante. Si, en cambio, obtenemos cualquier otro estado, podemos asegurar que la función es balanceada.
Implementación del algoritmo con Qiskit
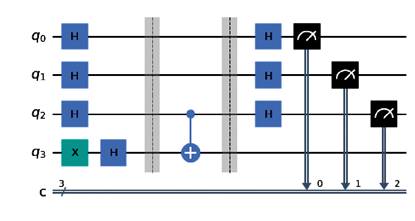
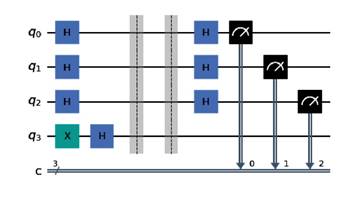
Implementaremos dos circuitos en la plataforma de IBM utilizando Qiskit. El primer circuito evaluará una función balanceada, y el segundo una función constante. El circuito creado tendrá cuatro cubits de entrada, los tres primeros serán los medios según indica el algoritmo.
Para implementar los circuitos con las respectivas funciones que nos atañen, y debido a que todas las entradas están inicializadas en el cubit |0〉 , aplicamos una compuerta X al último cubit, de esta forma hacemos que el cubit de entrada sea |0001〉 . Una vez realizado esto, podemos crear los dos circuitos para cada caso. Los circuitos creados con Qiskit se presentan en la Figura 2 para una función balanceada y Figura 3 para una función constante
En cada caso se realiza la medición de los tres primeros cubits una sola vez. Los resultados obtenidos de los circuitos de Figura 2 y Figura 3 son los representados en la Figura 4 y Figura 5 respectivamente.
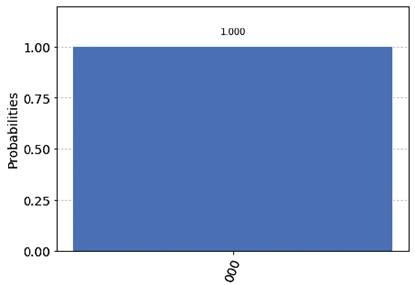
Al medir una sola vez los primeros tres cubits del circuito 2 el resultado es 100, como se mide al menos un uno, el algoritmo Deutsch-Jozsa nos dice que la función evaluada es balanceada. En cambio, para el circuito 3 notamos que el resultado de la medición es 000, es decir, todos los bits obtenidos son cero, y podemos concluir que la función es constante.
Figuras 4. Resultados obtenidos de los circuitos creados con Qiskit. 4) Para una función balanceada.
Cabe recalcar que los resultados se han obtenido realizando la medición una sola vez, lo cual demuestra la enorme ventaja de este algoritmo sobre el método clásico.
Conclusión
El algoritmo Deutsch-Jozsa es una muestra, bastante clara, del poder que tiene la computación cuántica gracias al “paralelismo”. Una acabada comprensión del funciona miento del mismo da rienda suelta a la imaginación y nos hace pensar en la posibilidad de la implementación de otros algoritmos cuánticos para realizar tareas mucho más relevantes que la simple discriminación entre dos tipos de funciones bien definidas, podrían servir como ejemplos el algoritmo de Grover, el cual es un algoritmo de búsqueda; el algoritmo de Shor, el cual permite encontrar los factores de un número de forma muy eficiente, entre otros.
Qiskit, por su parte, es una herramienta bastan- te útil para introducirse al mundo de la computación cuántica, y no queda nada más que esperar a ver todo lo que este tipo de iniciativas puede aportar, tanto en el campo de la ciencia como en la industria. El paralelismo que caracteriza a la computación cuántica es la clave de ese poder, el cual aún no ha sido totalmente aprovechado.











 uBio
uBio